دوال مثلثية

في الرياضيات، الدوال المثلثيَّة[1] أو التوابع المُثلثية[2] أو الاقترانات المثلثية (بالإنجليزية: Trigonometric Functions)‏، وتُسمَّى أيضاً الدوال الزاويَّة أو الدوال الدائريَّة[3] هي مجموعة من الدوال الحقيقيةٌ التي تربط زاوية مثلث قائم مع نسبة ضلعين من أضلاعه.[4][5][6] من الدوال المثلثيةِ الشهيرة والأساسيّة، دالة الجيب، ويرمزُ إليها بالكتابة اللاتينية $\sin$ ، ودالةُ جيبِ التمام، ورمزها $\cos$ ، ودالة الظل، ورمزها $\tan$ .[ملاحظة 1] مقاليب هذه الدوال هم دوالٌ مثلثيّةٌ أيضاً وهي: قاطع التمام والقاطع وظل التمام على التوالي.[1]لاحظ أن مقلوب دالة الجيب هو دالة القاطع التمام ومقلوب دالة جيب التمام هو دالة القاطع.

ميّز عن دالة مثلثية الشكل، وموجة مثلثية.

يعود حساب المثلثات إلى ما قبل الميلاد، تحديداً في مصر القديمة واليونان القديمة. وضع الرياضياتي طاليس مبرهنة طاليس في مصر في القرن السادس قبل الميلاد، ووضع الرياضياتي فيثاغورس مبرهنة فيثاغورس، حيث يشار إلى هاتين المبرهنتين بأنهما حجر الأساس لحساب المثلثات. بالإضافة إلى مصر واليونان، حقق علماء الحضارات الأخرى، بما في ذلك الصين والهند والدول الإسلامية والدول الأوروبية، تقدمًا ملحوظًا في علم المثلثات؛ فبرز الخوارزمي والبتاني وأبو الوفاء محمد البوزجاني وشين كوا وغوا شوجينغ وغيورغ يواخيم ريتيكوس وغيرهم.

يُمكن تعريفُ هذه الدوالِ على أنّها نسبةٌ بين أضلاعِ مُثلثٍ قائمٍ يَحتوي تلك الزاويةَ أَو بشكل أكثر عموميةٍ، إحداثياتٍ على دائرة الوحدة.[ملاحظة 2] عند الإشارة إلى المثلثات، غالباً يُقصدُ المثلثُ في السَطح المستوي. وذلك ليكون مجموعُ الزوايا $180^{\circ }$ دائماً.

هناك عدة تعاريف أخرى للدوال المثلثية، بما في ذلك التعريف بواسطة التكاملات ومتسلسلات القوى والمعادلات التفاضلية، لكل منها تطبيقه الخاص. على سبيل المثال، في التعريف بواسطة متسلسلة القوى، تُستخدم متسلسلة تايلور أو لوران على نطاق واسع في حساب القيم التقريبية للدوال. تسمح بعض التعريفات بتمديد مجال الدوال المثلثية الست إلى المستوى العقدي.

يكون متغير الدوال المثلثية عموما زاويةً وقد يكون أيضا عددًا حقيقيًا. كل دالة لديها خصائصها، بما في ذلك الزوجية والفردية، والدورية والاستمرارية والتعامد. التطبيق الرئيسي لهذه الدوال هو حساب أطوال الأضلاع وزوايا المثلث والعوامل الأخرى ذات الصلة. يستخدم هذا التطبيق على مدىً واسعٍ في علوم مختلفة مثل علم المساحة والملاحة ومجالات الفيزياء المختلفة. في علم المساحة، تتمثل في عملية التثليث التي تستخدم لحساب إحداثيات نقطة معينة والتي تُستخدم حاليًا في القياس البصري ثلاثي الأبعاد ^{[الإنجليزية]}؛ وفي الملاحة، في حساب إحداثيات السفن ورسم المسارات وحساب المسافات أثناء الملاحة؛ وفي الجغرافيا، حساب مسافة بين نقطتين على الكرة الأرضية، وتحديد إتجاه القبلة بحساب زاويتها بالنسبة للشمال؛ وفي البصريات، تستخدم أساسا في دراسة ظاهرة انكسار الضوء. الدوال المثلثية دوال دوريَّةٌ، أي أنها تُكرر قيمتها بعد فترة محددة؛ ولهذا فإنها تُستعمل لتمثيل الظواهرِ المتكررة كالموجات وهي الأساس الذي يرتكز عليه تحويل فورييه. عملية فورييه هي عمليةٌ رياضيةٌ تُستخدمُ لتحويل دالّةٍ رياضيةٍ بمتغير حقيقي وذات قيم مركّبة إلى دالّة أخرى من نفس الطراز. تشمل الاستخدامات الأخرى للدوال المثلثية في صناعة الطاقة الكهربائية والاتصالات، ويشمل هذا تطبيق دراسة التيارات المتناوبة والتضمين التي تعتمد على موجات جيبية.

تعريف الدوال

يوضح الجدول التالي تسميات مختلفة للدوال الست، بالإضافة إلى التسميات الإنجليزية والفرنسية ومجال تعريفهن ومستقراتهن (المجال المقابل).

التسمية العربية[7]	التسمية الإنجليزية[3]	التسمية الفرنسية[3]	الترميز بالحروف العربية [8][9]	الترميز بالحروف اللاتينية [1][10][11][12]	مجال التعريف[ملاحظة 3][13]	مستقر[13]
الجَيْب	Sine	Sinus	جا، جب	sin	جميع الأعداد الحقيقية	$[-1,1]$
جَيْب التَمَام	Cosine	Cosinus	جتا، تجب	cos	جميع الأعداد الحقيقية	$[-1,1]$
الظِل، الظل الأول، الظل القائم أو المنتصب أو المعكوس	Tangent	Tangente	ظا، ظل	tan	جميع أ.ح. ما عدا ${\frac {\pi }{2}}+k\pi$	جميع الأعداد الحقيقية
ظِل التمام، الظل الثاني أو المبسوط أو المستوي	Cotangent	Cotangente	ظتا، تظل	cot [ملاحظة 4]	جميع أ.ح. ما عدا $k\pi$	جميع الأعداد الحقيقية
القاطع، قطر الظل الأول	Secant	Sécante	قا	sec	جميع أ.ح. ما عدا ${\frac {\pi }{2}}+k\pi$	$]-\infty ,1]\cup [1,+\infty [$
قاطع التمام، قطر الظل الثاني، قطر الظل	Cosecant	Cosécante	قتا	csc [ملاحظة 5]	جميع أ.ح. ما عدا $k\pi$	$]-\infty ,1]\cup [1,+\infty [$

أصل تسمية الدوال

(1) رسم توضيحي لسبب تسمية دالة الجيب بهذا الإسم

(2) رسمٌ توضيحيٌّ لسبب تسمية الدوال، عند تمثيل الرياضياتيين المسلمين للدوال في دائرة الوحدة واعتبار نصف قطرها OD مقياسًا، فكانت النتيجة كما هي موضحة في الشكل.

استُمِدّت الكلمة الإنجليزية "Sine" [ملاحظة 6] من الكلمة اللاتينية "Sinus" التي تعني "انحناء، خليج"، وبشكل أكثر تحديداً "الطية المعلقة للجزء العلوي للّباس الروماني تُوجة"، "طوق الثوب"، التي تم اختيارها على أنها ترجمة لِمَا تم تفسيره على أنه ترجمة الكلمة العربية الفصيحة "جَيْب" في ترجمات القرن الثاني عشر لأعمال البتاني والخوارزمي إلى اللغة اللاتينية للقرون الوسطى.[ملاحظة 7] كان الاختيار مبنيًا على القراءة الخاطئة للكلمة العربية "جيب" التي هي تحريف للكلمة جِيبا التي نشأت في حد ذاتها كنقحرة للكلمة السنسكريتية जीवा / jīvā التي تُترجَم جنبًا إلى جنب برفقة مرادفها jyā / ज्या (المصطلح السنسكريتي لدالة الجيب) إلى "وتر قوس المحارب".[14] في القرن الحادي عشر، شرح أبو الريحان البيروني ذلك في كتابه القانون المسعودي:[15]

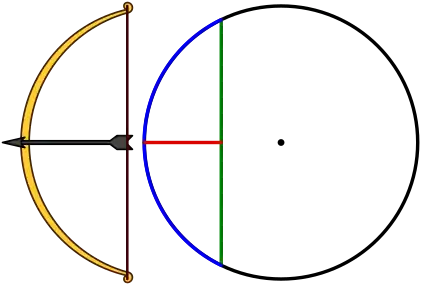
«إن هذه الصناعة إذا أريد إخراجها إلى الفعل بمزاولة الحساب فيها فالأعداد مفتقرة إلى معرفة أوتار قسي الدوائر، فلذلك سمى أهلها كتبها العلمية زيجات من الزيق الذي هو بالفارسية زه، أعني الوتر، وسموا أنصاف الأوتار جيوباً، وإن كان اسم الوتر بالهندية جيبا ونصفه جيبارد، ولكن الهند إذا لم يستعملوا غير أنصاف الأوتار أوقعوا اسم الكل على النصف تخفيفاً في اللفظ»

استُعملت مصطلح "جَيْب" في الأصل لوصف خط مستقيم مرسوم عموديًّا من أحد طرفي قوس على خط مستقيم آخر يمر بالطَّرف الآخر،[16] أما علاقتها بجيب الزاوية، فجيب الزاوية هو عبارة عن مقدار هذا الخط المستقيم في دائرة الوحدة، كما هو موضّح في الشكل (2).

أما عن الاسم العربي لدالة الـ"ظل"، فقد جاء من مقدار ما يصنعه ظل المقياس على سطح أفقي أثناء سقوط الضوء على المقياس بزاوية معيّنة، فنقول أن طول الظل تساوي n أضعاف المقياس،[14] وعند تمثيل الرياضياتيين المسلمين للدالة على دائرة الوحدة باعتبار نصف قطر الدائرة مقياسًا، فكانت النتيجة هي أنها عبارة عن خط مستقيم يمُس الدائرة، لهذا السبب، أطلق الغربيون (منهم توماس فينك)، على الظل اسم "Tangent" التي أتت من اللاتينية "tangens" التي تعني "يمُس".[17][18][ملاحظة 8]

بنفس الطريقة مثل طريقة دالة الظل، كانت النتيجة هي أن قيمة قُطْر الظِّل (التسمية القديمة لدالة القاطع) هي عبارة عن خط مستقيم يقطع الدائرة، لذا أُطلق عليها اسم "القاطع"،[18] من المحتمل أن الكلمة الإنجليزية secant التي استمدت من اللاتينية "secans" التي تعني "يَقْطَع"، كانت ترجمة للتسمية العربية "قاطع".[17][ملاحظة 8]

أما عن بادئة " $co-$ " (Cosine، Cotangent)، فقد عُثر عليها في كتاب العالم إدموند غونتر الذي يحمل عنوان "Triangulorum Canon" (صدر في عام 1620)، والذي يُعَرِّف Cosinus بأنها اختصار لـ sinus complementi التي استخدمت للإشارة إلى "جيب الزاوية المتممة لزاوية"؛[19] أما عن التسمية العربية "جيب التمام"، فهي استخدمت للإشارة إلى نفس الشيء، حيث أن كلمة "التمام" باللغة العربية تعني شيء متمم، مثلاً يقال في الهندسة أن الزاوية المتممة للزاوية 30 في المثلث قائم الزاوية هي 60 وذلك لأن مجموعهما يعطي 90،[14] التسمية العربية واللاتينية أتيا من السنسكريتية कोटिज्या "كوتي-جيا" بمعنى "جيب القوس المتمم لقوس"، حيث يعني الجذر الأول للمصطلح "نهاية قوس المحارب" أو "نهاية" بشكل عام، ولكنها تعني في حساب المثلثات "متمم القوس" أو بمعنى آخر "القوس المقابل للزاوية المتممة لزاوية"، لأن عند نشأة دوال الجيب وجيب التمام، كانت تعتبر أنذاك دوالاً لأقواس وليست دوالاً لزوايا هندسية.[14][20][21]

التاريخ

مقالة مفصلة: تاريخ حساب المثلثات

العصر القديم

اللوح المسماري المعروف باسم بليمبتون 322، يقال عنها أنها تحتوي على جدول القواطع لخمسة عشر زوايا تتراوح بين 45 و 30 درجة.

أبرخش، الملقب بـ "أبي حساب المثلثات"

عُثر على دليل على استخدام الدوال المثلثية في مختلف المجالات، وخاصة في علم الفلك، في العديد من النصوص التي تعود إلى ما قبل التاريخ، بما في ذلك تلك الموجودة في اليونان ومصر وربما في بلاد الرافدين.

استنادًا إلى أحد التفسيرات للوحة المسمارية بليمبتون 322 (حوالي 1900 قبل الميلاد)، أكد البعض أن البابليين القدماء لديهم جدول القواطع. ومع ذلك، هناك الكثير من الجدل حول ما إذا كان جدول ثلاثيات فيثاغورس، أو حل المعادلات التربيعية، أو جدول مثلثي.[22][23]

تعد مبرهنة طاليس من أقدم الأعمال المتعلقة بحساب المثلثات، درس طاليس في مصر في القرن السادس قبل الميلاد، وتوصل إلى طريقة جديدة لحل مشكلة حساب ارتفاع الهرم خوفو، والتي عرفت فيما بعد باسم مبرهنة طاليس. يمكن اعتبار مبرهنة فيثاغورس أيضا أنها حجر الأساس لحساب المثلثات.[24] أنشأ الفلكي والرياضياتي اليوناني أبرخش (180-125 قبل الميلاد) أول جدول مثلثي، وهو جدول خاص بدالة الوتر، لهذا السبب أطلق عليه اسم "أبي حساب المثلثات". وضع منيلاوس الإسكندري أساسا للمثلثات الكروية.[25] في القرن الثاني ميلادي، أنشأ عالم الفلك اليوناني بطليموس الإسكندري جدولا مثلثيا مفصلا للأوتار في الكتاب 1، الفصل 11 من المجسطي.[26]

الرياضيات الهندية

تمثال العالم الهندي أريابهاتا (476-550 م) في المركز المشترك بين الجامعات لعلم الفلك والفيزياء الفلكية ^{[الإنجليزية]} (IUCAA) في بونه، الهند. يقال عنه أنه هو أول من اكتشف دالة الجيب ووضع أول جدول لها.[14]

كانت دراسة الدوال المثلثية شائعة أيضًا في الهند. على سبيل المثال، في القرن الرابع والخامس الميلادي، في كتاب "سوريا سيدهانتا"، استُخدِم جدول لأنصاف الأوتار بدلاً من جدول الأوتار في علم الفلك التي تعادل حاليا دالة الجيب. عرّفت مجموعة من الكتب العلمية "سيدهانتا" أولاً الجيب علاقةً حديثة بين نصف زاوية ونصف وتر، وعرفت أيضًا جيب التمام، وسهم الزاوية (1 - جيب تمامها)، ودالة الجيب العكسية.[25] يمكن إسناد دالة الجيب مع جيب التمام وسهم الزاوية إلى كل الدوال "جيا" و"كوتي جيا" و"أوتكراما جيا" المستخدمة في علم الفلك الهندي للحقبة الجوبتية، عن طريق الترجمة من السنسكريتية إلى العربية ومن العربية إلى اللاتينية.[25][27]

كان بهاسكارا الثاني واحد من الأوائل الذين اكتشفوا النتائج المثلثية لـ $\sin \left(a+b\right)$ و $\sin \left(a-b\right)$ ، مثل: $\sin \left(a+b\right)=\sin a\cos b+\cos a\sin b$ ، كان ذلك في القرن الثاني عشر.[14]

خط مادهافا السانغماغرامي، في حوال عام 1400، خطوات مبكرة ومهمة في تحليل الدوال المثلثية بدلالة المتسلسلات غير المنتهية (طالع متسلسلات مادهافا).[28]

عصر الحضارة الإسلامية

طالع أيضًا: الرياضيات في عصر الحضارة الإسلامية

تعريف الظل، وظل التمام، والقاطع وقاطع التمام عند رياضياتِيِي عصر الحضارة الإسلامية. حيث أن القطعة المستقيمة AD تمثل المقياس (عمودي في الأعلى وأفقي في الأسفل)، والقطعة المستقيمة OD تمثل ظله

محمد بن جابر بن سنان البتاني (854-929 م)، هو أول من وضع النسب المثلثية في تاريخ الرياضيات

خلال القرن التاسع الميلادي، كانت الدوال المثلثية الست المستعملة في العصر الحديث جزءاً من الرياضيات المستعملة في الحضارة الإسلامية، كما كان قانون الجيب معروفاً، وكان يستعمل في معضلة حل المثلثات.[29] باستثناء دالتي الجيب وجيب التمام التي اعتمدت من الرياضيات الهندية[ملاحظة 9]، اكتُشِفَت الدوال المثلثية الأربع الأخرى من قبل علماء الرياضيات المسلمين، بما في ذلك الظل وظل التمام والقاطع وقاطع التمام؛ حيث تنسب أقدم الأعمال المتبقية إلى الخوارزمي والمروزي الذين اعتبروا الدوال الأربعة الأخيرة.[14]

في أوائل القرن التاسع الميلادي، أنتج محمد بن موسى الخوارزمي جداول دقيقة لدوال الجيب والجيب التمام ويقال أنه أنتج أول جدول للظلال، كما أنه أنتج نسخة معدلة من زيج السند هند (الحاوية لجدول الجيوب) التي استعملت لحل المعضلات الفلكية.[30] في حوالي عام 830، اكتشف أحمد بن عبد الله المروزي ظل التمام، وأنتج جداول الظل وظل التمام.[31][32]

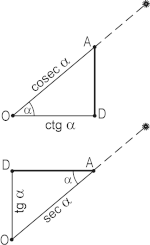
في البداية، عُرّفت الدوال الأربعة الأخيرة بطريقة تختلف عن الرياضيات الحديثة. حيث اعتبرت ظل التمام أنذاك طول ظل المقياس العمودي ارتفاعه 12 (أحيانًا 7) أصابع؛ في الأصل، استُخدمت هذه المفاهيم للحساب بالمزولة. كان يطلق على ظل المقياس الأفقي اسم "الظل المعكوس" التي تسمى ببساطة "الظل" حاليًا، وعلى ظل المقياس العمودي اسم "الظل المستوي".[33] كان يسمى وتر المثلث القائم المقابل (القطعة AO في الشكل على اليسار) "قطر الظل الأول" و"قطر الظل الثاني" التي يطلق عليها الآن القاطع وقاطع التمام، على التوالي.[34] في القرن العاشر ميلادي، قدم الفيلسوف وعالم الرياضيات الفارابي، في تعليقاته على المجسطي، تعريفات هذه الدوال الأربع بشكل مستقل عن المزولات، وتعريفها من خلال الجيب وجيب التمام في الدائرة المثلثية البطلمية التي طول نصف قطرها 60 (التي تساوي دائرة الوحدة، حيث أن نصف القطر معبر عنه بالنظام الستيني).[35] وضع محمد بن جابر البتاني النسب المثلثية لأول مرة والعلاقات الأساسية بين الدوال الست في القرن نفسه.[36] تم تحقيق التوحيد النهائي من قبل أبو الوفاء البوزجاني في النصف الثاني من القرن العاشر، والذي استخدم لأول مرة دائرة الوحدة لتعريف الدوال المثلثية، كما هو الحال في الرياضيات الحديثة.

ساهم محمد بن جابر البتاني في إدخال أنصاف الأوتار الهندية في الحسابات واستخدم لأول مرة مصطلحي "الجيب" و"جيب التمام" معرفاً إياهما بوصفهما أطوالاً بدلاً من نسب كما نعرفهما اليوم؛[37][38] كما أنه أنتج الجدول الأول لقواطع التمام لكل درجة من $1°$ إلى $90°$ ،[32][39] واكتشف أيضًا قانون جيب التمام للمثلثات الكروية.[40]

في القرن العاشر، اكتشف أبو الوفاء البوزجاني قانون الجيب للمثلثات الكروية،[41] واكتشف أيضا تلك المتطابقات المثلثية، حيث عبر الرياضياتيون اليونانيون عن تلك المتطابقات بدلالة الأوتار:[31]

\sin(a+b)=\sin(a)\cos(b)+\cos(a)\sin(b)

\cos(2a)=1-2\sin ^{2}(a)

\sin(2a)=2\sin(a)\cos(a)

طُوِّرت طريقة التثليث لأول مرة من قبل علماء الرياضيات المسلمين، الذين طبقوها على الاستخدامات العملية مثل مسح الأراضي والجغرافيا الإسلامية،[42] كما وصفها أبو الريحان البيروني في كتابه القانون المسعودي في أوائل القرن الحادي عشر. أدخل البيروني نفسه تقنيات التثليث لقياس حجم الأرض والمسافات بين الأماكن المختلفة،[43] كما أنه استخدم الرموز التالية للإشارة إلى الدوال: جا وجتا وظا وظتا وقا وقتا.[7] في نهاية القرن الحادي عشر، حل عمر الخيام معادلات من الدرجة الثالثة عن طريق الحلول العددية التقريبية التي تم الحصول عليها عن طريق استيفاء الجداول المثلثية. في القرن الثالث عشر، اعتبر نصير الدين الطوسي لأول مرة حساب المثلثات تخصّصًا منفصلاً عن علم الفلك،[44] وصاغ قانون الجيب للمثلثات المسطحة، كما أنه اكتشف قانون الظل.[45] قام غياث الدين الكاشي بالتعبير عن مبرهنة فيثاغورس المعممة (التي أصبحت تطلق عليها الآن "قانون جيب التمام") بدلالة جيب التمام بعدما أنشئت جداول لها التي أتاحت له صياغة المبرهنة، والبرهنة عليها في كتابه "مفتاح الحساب"، لذلك، أطلق الفرنسيين على هذا القانون اسم "مبرهنة الكاشي" (بالفرنسية: Théorème d'Al-Kashi)‏ تكريما له؛ وقدم بياناً صريحاً لهذا القانون في شكل مناسب للتثليث؛[46] مع العلم أن هذه المبرهنة تم التعبير عنها سابقًا من قبل العالم اليوناني إقليدس في كتابه الأصول، ولكن عدم وجود الدوال المثلثية آنذاك وكذلك الجبر أدى إلى استعمال مجموع وفرق المساحات؛[47] قام الكاشي أيضًا بصياغة المتطابقة التالية: $\sin 3\phi =3\sin \phi -4\sin ^{3}\phi \,\!$ واستخدمها لحساب جيب الزاوية 1° بوضع $\phi =1^{\circ }$ و $x=\sin 1^{\circ }$ ثم حل المعادلة من الدرجة الثالثة المتحصل عليها؛ ووصل إلى 16 منزلة عشرية. هذه الصيغة معروفة عند الغربيين بـ"صيغة فييت" ونسبوها إلى فرانسوا فييت عن طريق الخطأ، ولكن الكاشي هو أول من أكتشف تلك الصيغة.[48] في حوالي 1440، وضع الرياضياتي وحاكم الدولة التيمورية أولوغ بيك جداول دقيقة للجيب والظل ووصل إلى 9 أرقام عشرية بعد الفاصلة في نفس الوقت تقريبًا.[49]

الرياضيات الصينية

لم يدرس العلماء الصينيون حساب المثلثات كثيرًا. درس العالمان الصينيان شين كوا وغوا شوجينغ الدوال المثلثية. على سبيل المثال، في القرن الحادي عشر، وجد شين كيو علاقة تقريبية لحساب طول القوس s بدلالة قطر الدائرة d وعمق القوس v وطول الوتر c:[50] $s=c+{\frac {2v^{2}}{d}}$

النهضة الأوروبية وما بعدها

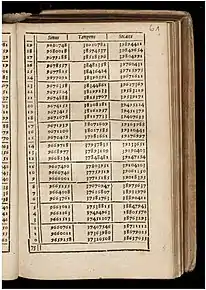
صفحة من كتاب يعود تاريخه إلى عام 1619 تحتوي على جدول للدوال التالية: الجيب، والظل والقاطع.

كانت أطروحات العالم الألماني ريغيومونتانوس (خاصةً كتابه عن المثلثات De triangulis omnimodis في 1464) وتعليقاته على المجسطي لبطليموس، هي أصل نهضة حساب المثلثات في أوروبا.[25] علّق في كتابه عن المثلثات:[44]

«أنت من تريد دراسة أشياء كبيرةً وعجيبةً، ومن تتعجب من حركة النجوم، عليك أن تدرس هذه المبرهنات حول المثلثات. معرفتك لهذه الأفكار ستفتح لك الباب لعلم الفلك كله ولبعض المعضلات الهندسية.»

استخدم عالم الرياضيات الفرنسي ألبرت جيرارد (1595 – 1632 م) لأول مرة الاختصارات sin، وcos، وtan في كتابه "Trigonométrie".[51]

ربما كان الكتاب Opus palatinum de triangulis لغيورغ يواخيم ريتيكوس، طالب كوبرنيكوس، الأول في أوروبا الذي عرف الدوال المثلثية مباشرة بدلالة المثلثات القائمة بدلاً من الدوائر، مع جداول لجميع الدوال المثلثية الست؛ أُنهي هذا العمل من قبل طالب ريتيكيوس فالنتينوس أوتو في عام 1596.[52]

أُدخِلت المصطلحات "Tangent" و"Secant" لأول مرة من قبل عالم الرياضيات الدنماركي توماس فينك في كتابه "Geometria rotundi".[53]

في مقال نُشر عام 1682، برهن غوتفريد لايبنتس على أن دالة الجيب $sin x$ ليست بدالة جبرية ل $x$ ، أي أنها دالة متسامية.[54]

كانت معظم مقدمة ليونهارت أويلر في كتاب analysin infinitorum (صدرت في عام 1748) عن تأسيس المعالجة التحليلية للدوال المثلثية في أوروبا، كما عرفها متسلسلاتٍ لانهائية ووضع صيغة أويلر، وعرفها كذلك اختصاراتٍ شبه حديثة (sin, cos, tang, cot, sec, cosec).[25]

في ستينيات القرن الثامن عشر، اخترع الإيطالي فينتشنزو ريكاتي الدوال الزائدية، وهي تلك الدوال التي تشبه لحدٍ كبيرٍ الدوال المثلثية.[55]

الدوال المثلثية التاريخية

هناك بعض الدوال الشائعة من الناحية التاريخية، ولكن نادراً ما تستخدم الآن، مثل دالة الوتر والسهم (يطلق عليها أيضا اسم "الجيب المنكوس"[56]) وسهم التمام ونصف السهم،[57] القاطع الخارجي وقاطع التمام الخارجي.[58]

\operatorname {crd} (\theta )=2\sin({\tfrac {\theta }{2}})

\operatorname {versin} (\theta )=1-\cos(\theta )=2\sin ^{2}({\tfrac {\theta }{2}})

\operatorname {coversin} (\theta )=1-\sin(\theta )=\operatorname {versin} \left({\frac {\pi }{2}}-\theta \right)

\operatorname {haversin} (\theta )={1 \over 2}\operatorname {versin} (\theta )=\sin ^{2}({\tfrac {\theta }{2}})

\operatorname {exsec} (\theta )=\sec(\theta )-1

\operatorname {excsc} (\theta )=\operatorname {exsec} \left({\frac {\pi }{2}}-\theta \right)=\csc(\theta )-1

وحدات قياس الزوايا

الدرجة: يعود استخدامها إلى عصور قديمة. تُحسبُ هذه القيمة عن طريق تقسيم دائرة إلى 360 جزءا متساويا، يرمز لها بقيمة متبوعة بدائرة صغيرة علوية.

الراديان أو الزاوية نصف القطرية أو التقدير الدائري: يساوي الزاوية المقابلة لقوس طوله مطابق لطول نصف قطر الدائرة، دورة كاملة هي زاوية مقدارها $2 π$ راديان.[59][60]

الغراد: تعادل 1/400 من قياس الدائرة الكاملة، أو 100 جزء من الزاوية القائمة، يرمز لها بقيمة متبوعة بحرف "g" صغير علوي.[61]

الدورة: تعادل 360° أو $2π$ راديان.

دقيقة وثانية القوس: هي وحدات فرعية للدرجة، تستخدم على مدًى واسع في نظام الاحداثيات الجغرافية.[62]

دقيقة القوس: تساوي 1/60 درجة أي 0.016°،[ملاحظة 10] يرمز لها بقيمة متبوعة بالبرايم ( ' ).
ثانية القوس: تساوي 1/3600 درجة أي 0.00027°،[ملاحظة 10] يرمز لها بقيمة متبوعة بعلامة التنصيص ( " ).

وحدة	مقدار
درجة	0°	30°	45°	60°	90°	180°	270°	360°
راديان	0	$π$ /6	$π$ /4	$π$ /3	$π$ /2	$π$	3 $π$ /2	2 $π$
غراد	0^g	100/3^g	50^g	200/3^g	100^g	200^g	300^g	400^g
دورة	0	1/12	1/8	1/6	1/4	1/2	3/4	1

راديان مقابل درجات

في التطبيقات الهندسية، يكون متغير دالة مثلثية عمومًا هو مقياس الزاوية. لهذا الغرض، كل الوحدات الزاوية مناسبة، ويتم قياس الزوايا في أغلب الحالات بالدرجات.[63]

عند استخدام دالة مثلثية في حساب التفاضل والتكامل، فإن متغيرهم ليست عمومًا زاوية، لكنه بالأحرى عدد حقيقي. في هذه الحالة، من الملائم أكثر التعبير عن المتغير المثلثي طولَ قوس دائرة الوحدة المحددة بزاوية مع مركز الدائرة كرأس. لذلك، يُستخدم الراديان وحدةً للزاوية.[59][63][64]

ميزة كبيرة للراديان هي أن العديد من الصيغ تكون أبسط بكثير عند استخدامها، عادة كل الصيغ المتعلقة بالمشتقات والتكاملات.[63]

هذا هو بالتالي اصطلاح عام، عندما تكون وحدة الزاوية غير محددة بوضوح، يتم التعبير دائمًا عن متغيرات الدوال المثلثية بالراديان.

التعريف باستعمال المثلث قائم الزاوية

طالع أيضًا: مثلث قائم

يوضح الشكل المقابل مثلثًا قائما [ملاحظة 11] يتكون من ثلاثة أضلاع a و b و c وزوايا A و B و C. الزاوية C قياسها $90^{\circ }$ وزاويتان أخريان حادتان ومتتامتان، بمعنى آخر، مجموع قياس الزاويتين يساوي $90^{\circ }$ أو π/2 راديان.

يسمى الضلع المقابل للزاوية C الوتر (كما هو موضح في الشكل المقابل). عند اعتبار الزاوية A، يسمى الضلعان اللذان يشكلان الزاوية القائمة بالضلع المجاور للزاوية A (الضلع AC) والضلع المقابل للزاوية A (الضلع BC).

تعرف الدوال المثلثية الرئيسية للزاوية A بـ:[1][65]

جيب الزاوية: هو النسبة بين الضلع المقابل والوتر. أي حاصل قسمة الضلع المقابل للزاوية على وتر المثلث القائم الزاوية، بمعنى آخر: $\sin A={\frac {a}{\,c\,}}$
جيب تمام الزاوية: هو النسبة بين الضلع المحادي للزاوية ووتر المثلث، بتعبير آخر: $\cos A={\frac {b}{\,c\,}}$
ظل الزاوية: يساوي النسبة بين الضلع المقابل للزاوية والضلع المجاور لها، أي:

\tan A={\frac {a}{\,b\,}}={\frac {a}{\,c\,}}\times {\frac {c}{\,b\,}}={\frac {a}{\,c\,}}\div {\frac {b}{\,c\,}}={\frac {\sin A}{\cos A}}

وفقًا للتشابه الهندسي، إذا كان لمثلثين زوايا متساوية، فإن نسبة أضلاعهما متساوية. ونتيجة لذلك، تعتمد الدوال المثلثية التي تمثل النسبة بين طولي ضلعين على مقدار الزاوية فقط، يعني أن الدوال لا تتغير قيمتها مع التغير في طول الأضلاع.

بالنسبة للزاوية B، يمكننا أيضًا حساب الدوال المثلثية. الضلع المجاور للزاوية B (الضلع a) هو الضلع المقابل للزاوية A والضلع المقابل B (الضلع b) هو أيضًا الضلع المجاور لـ A، لذلك يمكن القول أن جيب الزاوية B هي جيب التمام الزاوية A والعكس صحيح. علاقة الجيب وجيب التمام بالزوايا المتتامة رياضيا هي كما يلي:[65]

\sin A=\cos B=\cos \left({\frac {\pi }{2}}-A\right)=\cos \left(90^{\circ }-A\right)

\cos A=\sin B=\sin \left({\frac {\pi }{2}}-A\right)=\sin \left(90^{\circ }-A\right)

كلما ازدادت قيمة الزاوية A من صفر إلى 90 درجة، تناقص طول الضلع المجاور تدريجياً ويزداد طول الضلع المقابل. عندما تقترب هذه القيمة من 90 درجة، فإن طول الضلع المجاور يقترب من الصفر. نتيجة لذلك، يؤول جيب تمام الزاوية A إلى الصفر. من ناحية أخرى، فإن طول الضلع المقابل يكون مطابقا للوتر (وفقًا لمبرهنة فيثاغورس، فإن الوتر دائمًا أكبر من الضلعين الآخرين). ونتيجة لذلك، جيب الزاوية A يساوي واحدا. بشكل عام، تتراوح قيمة الجيب وجيب التمام في المثلث القائم، بين الصفر والواحد. يمكن تتبع تغيرات ظل الزاوية بنفس الطريقة. عند حوالي 90 درجة، يؤول ظل الزاوية A إلى اللانهاية، وعندما تقترب من الصفر، تقترب قيمته من الصفر، وبالتالي فإن قيمة ظل الزاوية هي عدد موجب (من الصفر إلى اللانهاية).

يمكن تعريف الدوال المثلثية الثلاث الأخرى بأنها مقاليب الدوال الثلاث المذكورة أعلاه:[65]

ظل تمام الزاوية: هو النسبة بين الضلع المجاور على الضلع المقابل، أي: $\cot A={\frac {b}{\,a\,}}={\frac {\cos A}{\sin A}}={\frac {1}{\tan A}}$
قاطع الزاوية: هو النسبة بين الوتر على الضلع المجاور، أي: $\sec A={\frac {c}{\,b\,}}={\frac {1}{\cos A}}$
قاطع تمام الزاوية: هو النسبة بين الوتر على الضلع المقابل، أي: $\csc A={\frac {c}{\,a\,}}={\frac {1}{\sin A}}$

نطبق العلاقة بين الزوايا المتتامة، كما هو مذكور أعلاه في حالة الجيب و جيب التمام، أيضًا على الدوال المثلثية الأخرى:[65]

\tan A=\cot B=\cot \left({\frac {\pi }{2}}-A\right)=\cot \left(90^{\circ }-A\right)

\cot A=\tan B=\tan \left({\frac {\pi }{2}}-A\right)=\tan \left(90^{\circ }-A\right)

\sec A=\csc B=\csc \left({\frac {\pi }{2}}-A\right)=\csc \left(90^{\circ }-A\right)

\csc A=\sec B=\sec \left({\frac {\pi }{2}}-A\right)=\sec \left(90^{\circ }-A\right)

ملخص العلاقات

تُلخص العلاقة بين الدوال المثلثية وأضلاع المثلث القائم بالعلاقات التالية:

$sin A = المقابل / الوتر$ ، $cos A = المجاور / الوتر$ ، $tan A = المقابل / المجاور$ ، $cot A = المجاور / المقابل$ ، $sec A = الوتر / المجاور$ ، $csc A = الوتر / المقابل$

التعريف باستعمال دائرة الوحدة

طالع أيضًا: دائرة وحدة

(1) في هذا الرسم، الدوال المثلثية الستة لزاوية اختيارية θ ممثلة إحداثياتٍ ديكارتية للنقاط المتعلقة بدائرة الوحدة. الإحداثيات الصادية لكل من

A

و

B

و

D

هن

sin θ

و

tan θ

و

csc θ

على التوالي. في حين أن الإحداثيات السينية لكل من

A

و

C

E

هن

cos θ

و

cot θ

و

sec θ

على التوالي.

(2) رسمٌ توضيحيٌّ للإنشاءات الهندسية لمختلف الدوال المثلثية من الوتر

AD

الذي يصنع زاوية

\theta

مع محور السينات[ملاحظة 12] في دائرة الوحدة. بالإضافة إلى استعمال الدوال المثلثية الشائعة الحالية:

\sin ,\cos ,\tan ,\csc ,\sec ,\cot

فإنَّ الشكل يظهرُ بعضَ الدوالِ المثلثيّةِ التي هُجِرَ استعمالُها مثل:

{\text{cvs, excsc, crd, exsec, versin}}

.

(3) يسرد مساعد الذاكرة "All science teachers (are) crazy" إشارات الدوال المثلثية من الربع الأول إلى الربع الرابع.[59][66]

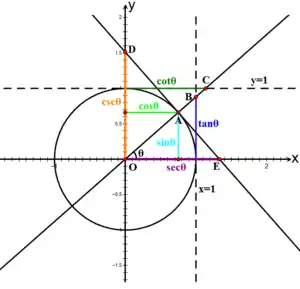
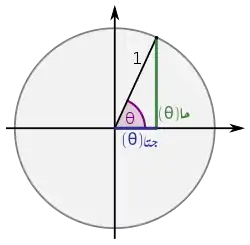
يمكنُ تعريفِ الدوالِ المثلثيةِ: الجيب وجيب التمام والظل ومقلوباتها، بقيمِ إحداثياتِ النقاطِ على المستوى الإقليدي المرتبطةِ بدائرة الوحدة. دائرة الوحدة هي دائرة نصف قطرها وحدةٌ واحدةٌ ومركزها نقطة الأصل. رغم أن تعريفات المثلثِ قائمِ الزاوية تسمحُ بتعريفِ الدوالِ المثلثيةِ للزوايا بينَ $0$ و ${\textstyle {\frac {\pi }{2}}}$ راديان فقط، إلا أنَّ تعريفاتِ دائرةِ الوِحدةِ تُعمّمُ ذلك وتمدد مجال الدوال المثلثية لتسمحَ بجميع الأعداد الحقيقية الموجبةِ والسالبةِ.[67][68]

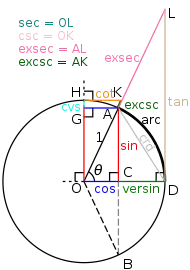
تُعطى تعريفات الدوال المثلثية من تقاطع مستقيمات مرتبطة بزاوية واقعةٍ على نقطة الأصل. إذا قطعَ الشعاعُ المنطلق من نقطة الأصل بزاويةَ $\theta$ [ملاحظة 13] دائرةَ الوحدةِ في النقطة $A=(x,y)$ فإنّ الدالةُ $\cos \theta$ تُعرّف على أنها الإحداثي $x$ [ملاحظة 14] والدالة $\sin \theta$ هي الإحداثي $y$ [ملاحظة 15] لنقطة التقاطع. وبمعنى آخر فإنَّ: $(x,y)=(\cos \theta ,\sin \theta )$ . وبرسم مماسٍ من النقطة $(x,y)$ يقطعُ محورَي السينات[ملاحظة 12] والصادات[ملاحظة 16] في النقطتين $E=(a,0),F=(0,b)$ على الترتيب، فإنَّ $a=\sec \theta ,b=\csc \theta$ .

يتطابقُ هذا التعريفُ مع تعريفِ المثلث قائم الزاوية في الفترة $(0,{\frac {\pi }{2}})$ باعتبار أنَّ نصفَ قطرِ دائرة الوحدة $OA=r$ هو وترٌ للمثلث القائم. ولأنّ كل نقطة $P=(x_{0},y_{0})$ على دائرة الوحدة تُحقّق $x^{2}+y^{2}=1$ من مبرهنة فيثاغورس في المثلث القائم $\triangle OCA$ ، فإنَّ تعريف الدوال المثلثية على أنها الإحداثيات $x,y$ يُنتِجُ متطابقة فيثاغورس: $\cos ^{2}\theta +\sin ^{2}\theta =1$ .[5][67] وأخيراً فإنَّ المسافات $AF,AE$ تُعرّفُ على أنّها الدوال المثلثية: $\cot {\theta },\tan {\theta }$ على الترتيب. بشكلٍ مُشابهٍ للاستنتاج السابق، يمكن تطبيق مبرهنة فيثاغورس في بقية المثلثات القائمة $\triangle OAF,\triangle OAE,\triangle OEF$ للوصول إلى متطابقات فيثاغورس الخاصة ببقية المتطابقات المثلثية. ومن تشابه هذه المثلثات القائمة السابقة، تُعطى العلاقات التي تربط بين جميع الدوال المثلثية كالآتي:[69]

\tan \theta ={\frac {\sin \theta }{\cos \theta }},\quad \cot \theta ={\frac {\cos \theta }{\sin \theta }},\quad \sec \theta ={\frac {1}{\cos \theta }},\quad \csc \theta ={\frac {1}{\sin \theta }}.

بما أنَّ دوراناً بزاوية $\pm 2\pi$ لا يُغير موضعَ الشكلِ ولا حجمَهُ، فإن النقاط $F,A,E$ ستبقى نفسها بالنسبة لزاويتين فرقَهُما مضاعف صحيح لـ $2\pi$ . وعلى ذلكَ، الدوال المثلثية هن دوالٌ دورية ذات دورة بطول $2\pi$ . بمعنى آخر، المساواةَ $\sin \theta =\sin \left(\theta +2k\pi \right)$ و $\cos \theta =\cos \left(\theta +2k\pi \right)$ صالحةٌ لأي زاوية $\theta$ ولأي عدد صحيح $k$ . ينطبق الشيء ذاته على الدوال المثلثية الأربع الأخرى.

تشير ملاحظة إشارة ورتابة دوال الجيب وجيب التمام والقاطع وقاطع التمام في الأرباع الأربعة إلى أن $2π$ هي أصغر قيمة تكون دورية لها، أي $2π$ هي الدورة الأساسية لتلك الدوال. إلا أن بعد الدوران بزاوية $π$ ، تعود النقطتان B وC إلى موضعهما الأصلي (الصورة (1))، بحيث تكون دالتا الظل وظل التمام لها دورة أساسية $π$ .[1]

الدوران

يمكن الحصول على الدوال المثلثية للزوايا الأكبر من 90° باستخدام علاقات الدوران حول مركز الدائرة. أيضًا، يمكن حساب الزوايا الأصغر من الصفر بالانعكاس حول المحور الأفقي. يوضح الجدول التالي كل العلاقات المثلثية:

انعكاس حول المحور الأفقي[70]	دوران بزاوية π/2	دوران بزاوية π	دوران بزاوية 2kπ (مع k عدد صحيح)	انعكاس حول المحور العمودي
$\sin(-\theta )=-\sin \theta$	$\sin(\theta +{\tfrac {\pi }{2}})=+\cos \theta$	$\sin(\theta +\pi )=-\sin \theta$	$\sin(\theta +2k\pi )=+\sin \theta$	$\sin(\pi -\theta )=\sin \theta$
$\cos(-\theta )=+\cos \theta$	$\cos(\theta +{\tfrac {\pi }{2}})=-\sin \theta$	$\cos(\theta +\pi )=-\cos \theta$	$\cos(\theta +2k\pi )=+\cos \theta$	$\cos(\pi -\theta )=-\cos \theta$
$\tan(-\theta )=-\tan \theta$	$\tan(\theta +{\tfrac {\pi }{2}})=-\cot \theta$	$\tan(\theta +\pi )=+\tan \theta$	$\tan(\theta +2k\pi )=+\tan \theta$	$\tan(\pi -\theta )=-\tan \theta$
$\cot(-\theta )=-\cot \theta$	$\cot(\theta +{\tfrac {\pi }{2}})=-\tan \theta$	$\cot(\theta +\pi )=+\cot \theta$	$\cot(\theta +2k\pi )=+\cot \theta$	$\cot(\pi -\theta )=-\cot \theta$
$\sec(-\theta )=+\sec \theta$	$\sec(\theta +{\tfrac {\pi }{2}})=-\csc \theta$	$\sec(\theta +\pi )=-\sec \theta$	$\sec(\theta +2k\pi )=+\sec \theta$	$\sec(\pi -\theta )=-\sec \theta$
$\csc(-\theta )=-\csc \theta$	$\csc(\theta +{\tfrac {\pi }{2}})=+\sec \theta$	$\csc(\theta +\pi )=-\csc \theta$	$\csc(\theta +2k\pi )=+\csc \theta$	$\csc(\pi -\theta )=\csc \theta$

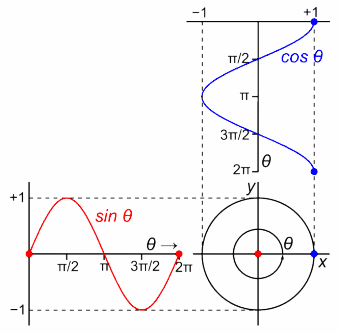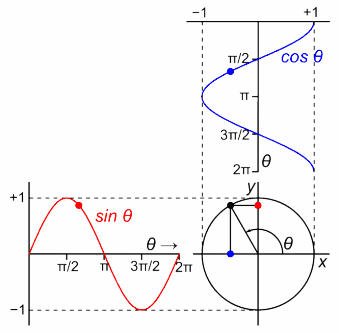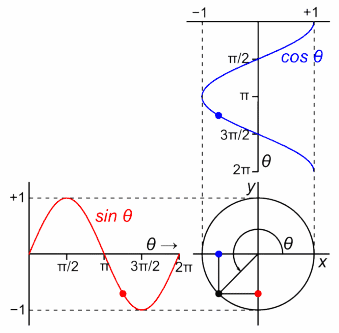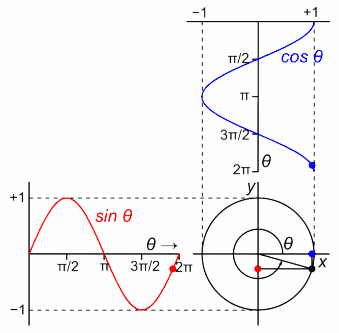رسم دالتي الجيب وجيب التمام باستخدام دائرة الوحدة
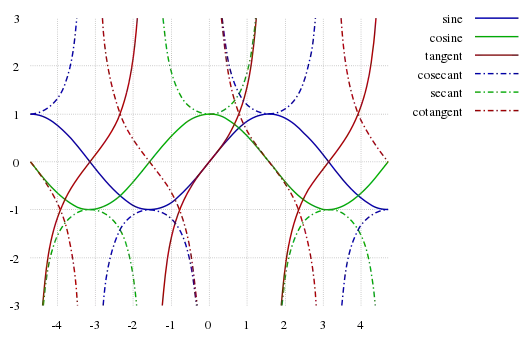الدوال المثلثية: الجيب، جيب التمام، الظل، قاطع التمام (منقط)، القاطع (منقط)، ظل التمام (منقط).

القيم الجبرية

مقالة مفصلة: قيم جبرية دقيقة لثوابت مثلثية

دائرة الوحدة

رسم توضيحي لكيفية حساب جيب زاوية مقدارها 30 درجة باستخدام مثلث متساوي الأضلاع.

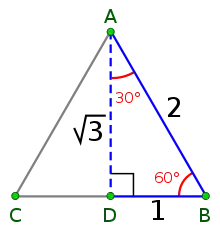
بالنسبة لبعض الزوايا، يمكن الحصول على قيم الدوال المثلثية بسهولة، تدعى هذه الزوايا: الزوايا الخاصة أو الزوايا الشهيرة.

إذا كان مقدار الزاوية يساوي 0°، فإن جيبها يساوي 0 وجيب التمام يساوي 1. وإذا كان مقدار الزاوية يساوي 90°، يصبح جيب التمام يساوي 0 والجيب يساوي 1، بتعبير آخر:

\sin 0^{\circ }=\cos 90^{\circ }=0

\sin 90^{\circ }=\cos 0^{\circ }=1

المثلث القائم ذو زاوية $45°$ له زاوية حادة أخرى تبلغ $45°$ أيضا، يطلق على هذا المثلث اسم مثلث قائم ومتساوي الساقين. في هذا المثلث، بناءً على مبرهنة فيثاغورس، طول الوتر يساوي $\sqrt2$ مرة طول كل من الساقين، إذن:

\sin 45^{\circ }=\cos 45^{\circ }={\frac {\sqrt {2}}{2}}

\tan 45^{\circ }=\cot 45^{\circ }=1

باستخدام خصائص مثلث متساوي الأضلاع (الشكل المقابل)، يمكن إظهار أن الضلع المقابل للزاوية 30° هو نصف طول الوتر، إذن:

\sin 30^{\circ }=\cos 60^{\circ }={\frac {1}{2}}

وبالمثل، يتم الحصول على طول الضلع الآخر باستخدام مبرهنة فيثاغورس، الذي يساوي $\sqrt3 / 2$ ، نتيجة لذلك:

\sin 60^{\circ }=\cos 30^{\circ }={\frac {\sqrt {3}}{2}}

إن كتابة البسوط جذورا تربيعية للأعداد الصحيحة غير السالبة المتتالية، مع مقام يساوي 2، توفر طريقة سهلة لتذكر القيم.[71]

تنص مبرهنة نيفن على أن القيم النسبية الوحيدة لـθ التي تتواجد في المجال $0^{\circ }\leq \theta \leq 90^{\circ }$ والتي يكون جيبها عدداً نسبياً هي الزوايا ذات القيم 0 و30 و90 درجة.[72] تمتد المبرهنة أيضًا إلى الدوال المثلثية الأخرى وإلى بعض الزوايا.[73] بالنسبة للقيم النسبية لـ θ، فإن القيم النسبية الوحيدة للجيب أو جيب التمام هي 0 و ±1/2 و ±1؛ والقيم النسبية الوحيدة للقاطع أو قاطع التمام هي ±1 و ±2؛ والقيم النسبية الوحيدة للظل أو ظل التمام هي 0 و ±1.[74]

مثل هذه التعبيرات البسيطة غير موجودة عمومًا للزوايا الأخرى التي تعتبر مضاعفات نسبية لزاوية مستقيمة. بالنسبة للزاوية التي تقاس بالدرجات، وهي من مضاعفات العدد 3، قد يتم التعبير عن الجيب وجيب التمام بدلالة الجذور التربيعية، طالع قيم جبرية دقيقة لثوابت مثلثية.[75] وبالتالي قد يتم انشاء هذه القيم للجيب وجيب التمام بواسطة المسطرة والفرجار.

بالنسبة لزاوية عدد صحيح بالدرجات، يمكن التعبير عن الجيب وجيب التمام بدلالة الجذور التربيعية والجذر التكعيبي لعدد مركب غير حقيقي.[76] تسمح نظرية غالوا بإثبات أنه إذا لم تكن الزاوية مضاعف $3°$ ، فإن الجذور التكعيبية غير الحقيقية لا يمكن تجنبها.

بالنسبة للزاوية التي تقاس بالدرجات وهي عدد نسبي، الجيب وجيب التمام هما عددان جبريان، يمكن التعبير عنهما بدلالة الجذور النونية.[76]

بالنسبة للزاوية التي تقاس بالدرجات وهي عدد غير كسري، إما أن تكون الزاوية أو الجيب وجيب التمام عددين متساميين. إنها لازمة مبرهنة باكر، ثُبتت في عام 1966.[77]

القيم الجبرية البسيطة

يلخص الجدول التالي أبسط القيم الجبرية للدوال المثلثية.[78] يمثل الرمز $\infty$ النقطة عند اللانهاية على الخط الحقيقي الممتد بشكل إسقاطي؛ إنها غير مؤشَّرة، لأنها عندما يظهر في الجدول، تؤول الدالة المثلثية المقابلة إلى $+\infty$ في جهة، وإلى $-\infty$ في جهة أخرى، عندما يؤول المتغير إلى القيمة في الجدول.

راديان	$0$	${\frac {\pi }{12}}$	${\frac {\pi }{8}}$	${\frac {\pi }{6}}$	${\frac {\pi }{4}}$	${\frac {\pi }{3}}$	${\frac {3\pi }{8}}$	${\frac {5\pi }{12}}$	${\frac {\pi }{2}}$
درجة	$0^{\circ }$	$15^{\circ }$	$22.5^{\circ }$	$30^{\circ }$	$45^{\circ }$	$60^{\circ }$	$67.5^{\circ }$	$75^{\circ }$	$90^{\circ }$
$\sin$	$0$	${\frac {{\sqrt {6}}-{\sqrt {2}}}{4}}$	${\frac {\sqrt {2-{\sqrt {2}}}}{2}}$	${\frac {1}{2}}$	${\frac {\sqrt {2}}{2}}$	${\frac {\sqrt {3}}{2}}$	${\frac {\sqrt {2+{\sqrt {2}}}}{2}}$	${\frac {{\sqrt {6}}+{\sqrt {2}}}{4}}$	$1$
$\cos$	$1$	${\frac {{\sqrt {6}}+{\sqrt {2}}}{4}}$	${\frac {\sqrt {2+{\sqrt {2}}}}{2}}$	${\frac {\sqrt {3}}{2}}$	${\frac {\sqrt {2}}{2}}$	${\frac {1}{2}}$	${\frac {\sqrt {2-{\sqrt {2}}}}{2}}$	${\frac {{\sqrt {6}}-{\sqrt {2}}}{4}}$	$0$
$\tan$	$0$	$2-{\sqrt {3}}$	${\sqrt {2}}-1$	${\frac {\sqrt {3}}{3}}$	$1$	${\sqrt {3}}$	${\sqrt {2}}+1$	$2+{\sqrt {3}}$	$\infty$
$\cot$	$\infty$	$2+{\sqrt {3}}$	${\sqrt {2}}+1$	${\sqrt {3}}$	$1$	${\frac {\sqrt {3}}{3}}$	${\sqrt {2}}-1$	$2-{\sqrt {3}}$	$0$
$\sec$	$1$	${\sqrt {6}}-{\sqrt {2}}$	${\sqrt {2}}{\sqrt {2-{\sqrt {2}}}}$	${\displaystyle {\frac {2{\sqrt {3}}}{3}}}$	${\sqrt {2}}$	$2$	${\sqrt {2}}{\sqrt {2+{\sqrt {2}}}}$	${\sqrt {6}}+{\sqrt {2}}$	$\infty$
$\csc$	$\infty$	${\sqrt {6}}+{\sqrt {2}}$	${\sqrt {2}}{\sqrt {2+{\sqrt {2}}}}$	$2$	${\sqrt {2}}$	${\displaystyle {\frac {2{\sqrt {3}}}{3}}}$	${\sqrt {2}}{\sqrt {2-{\sqrt {2}}}}$	${\sqrt {6}}-{\sqrt {2}}$	$1$

حساب التفاضل والتكامل

الدوال المثلثية هي دوال قابلة للتفاضل. هذا ليس واضحا على الفور من التعاريف الهندسية المذكورة أعلاه. علاوة على ذلك، فإن الاتجاه الحديث في الرياضيات هو بناء هندسة رياضية من حساب التفاضل والتكامل بدلاً من العكس. لذلك، باستثناء في المستوى الأساسي، يتم تعريف الدوال المثلثية باستخدام طرق حساب التفاضل والتكامل.

لتعريف الدوال المثلثية داخل حساب التفاضل والتكامل، هناك عدة امكانيات، منها التعريف باستخدام متسلسلة القوى أو المعادلات التفاضلية. هذه التعريفات الأخيرة متكافئة لأن انطلاقا من واحد منهم، من السهل البدء في استرداد التعريفات الأخرى كخاصية. ومع ذلك، يعتبر التعريف من خلال المعادلات التفاضلية أكثر طبيعية إلى حد ما، لأنه على سبيل المثال، قد يبدو اختيار معاملات متسلسلة القوى كله اختياري، ومتطابقة فيثاغورس هي أسهل بكثير لاستنتاج من المعادلات التفاضلية.

الاشتقاق والمكاملة

المشتقات الأولى والثانية للدوال المثلثية مع مشتقاتها العكسية هي كما يلي:

دالة	مشتقها الأول[60]	مشتقها الثاني	مشتقها من الرتبة n[79]	تكامل[59]
$\sin(x)$	$\cos(x)$	$-\sin(x)$	$\sin(x+{\frac {n\pi }{2}})$	$-\cos(x)$
$\cos(x)$	$-\sin(x)$	$-\cos(x)$	$\cos(x+{\frac {n\pi }{2}})$	$\sin(x)$
$\tan(x)$	$\sec ^{2}(x)$	$2\sec ^{2}(x).\tan(x)$	معقد[80]	$-\ln \|\cos(x)\|$
$\cot(x)$	$-\csc ^{2}(x)$	$2\csc ^{2}(x).\cot(x)$	معقد[80]	$\ln \|\sin(x)\|$
$\sec(x)$	$\sec(x).\tan(x)$	$\sec(x)(\sec ^{2}(x)+\tan ^{2}(x))$	معقد[80]	$\ln \|\sec(x)+\tan(x)\|$
$\csc(x)$	$-\csc(x).\cot(x)$	$\csc(x)(\csc ^{2}(x)+\cot ^{2}(x))$	معقد[80]	$-\ln \|\csc(x)+\cot(x)\|$

تعريف بواسطة التكامل

يمكن الحصول على تعريف آخر استنادا إلى الطول الدقيق لقوس الدائرة. باعتبار معادلة النصف العلوي للدائرة $y={\sqrt {1-x^{2}}}$ ، يمكننا إيجاد العلاقة بين الزاوية $\theta$ و $\sin \theta$ وفقًا للمعادلة التالية:[81][82]

\int _{0}^{\sin \theta }{\sqrt {1+\left({d \over dx}{\sqrt {1-x^{2}}}\right)^{2}}}dx=\int _{0}^{\sin \theta }{\frac {dx}{\sqrt {1-x^{2}}}}=\theta

حيث تنتمي الزاوية θ إلى المجال $0\leq \theta \leq \pi /2$ .

التعريف بواسطة المعادلات التفاضلية

الجيب وجيب التمام هما من الدوال الفريدة من نوعها التي تقبل التفاضل، بحيث:

{\begin{aligned}{\frac {d}{dx}}\sin x&=\cos x,\\{\frac {d}{dx}}\cos x&=-\sin x,\\\sin 0&=0,\\\cos 0&=1.\end{aligned}}

كل من دالتي الجيب والجيب التمام تحققان المعادلة التفاضلية التالية:

y''=-y

(معادلتها المميزة هي

m^{2}+1=0

، جذرها هي وحدة تخيلية موجبة أو سالبة

\pm i

) بتعبير آخر، كل منهما تساوي مقابل مشتقتها من الدرجة الثانية.

الجيب هو الحل الوحيد لهذه المعادلة التي تحقق الشروط التالية:[83]

{\begin{cases}y(0)=0\\[2pt]y\,'(0)=1\end{cases}}

جيب التمام هو الحل الوحيد لهذه المعادلة التي تحقق الشروط التالية:[83]

{\begin{cases}y(0)=1\\[2pt]y\,'(0)=0\end{cases}}

بتطبيق قاعدة ناتج القسمة على تعريف ظل الزاوية باعتباره نسبة بين الجيب وجيب التمام، يحصل الفرد على أن دالة الظل تحقق:

{\frac {d}{dx}}\tan x=1+\tan ^{2}x.

إذن، دالة الظل هي حل للمعادلة التفاضلية التالية:

y'=1+y^{2}

نعتبر المعادلة التفاضلية من الدرجة الثانية التالية: $ay''+by'+cy=0$

إن حل هذه المعادلة هي الدالة الأسية من الشكل

y=A_{1}e^{m_{1}x}+A_{2}e^{m_{2}x}

، حيث $m_{1}$ و $m_{2}$ هما جذور المعادلة المميزة للمعادلة (

am^{2}+bm+c=0

). أيضا

A_{1}

و

A_{2}

هي ثوابت كيفية بناءً على الشروط الأولية.

إذا كانت المعادلة المميزة لها جذور عقدية، فإن حل هذه المعادلة هي الدالة الأسية العقدية:

y=A_{1}.e^{(\alpha +i\beta )x}+A_{2}.e^{(\alpha -i\beta )x}

حيث

\alpha

هو الجزء الحقيقي و

\beta

هو الجزء التخيلي لجذر المعادلة المميزة. استنادًا إلى صيغة أويلر، يمكننا تحويل الدالة الأسية العقدية إلى دالتي الجيب وجيب التمام، لذلك في حالة الجذور العقدية، ستتضمن حل المعادلة التفاضلية دوال مثلثية:[84]

y=A_{1}.e^{\alpha x}\cos \beta x+A_{2}.e^{\alpha x}\sin \beta x

باستعمال المتسلسلات

دالة الجيب (باللون الأزرق) تحسب بصفة تقريبية اقترابا كبيرا بواسطة متعددة الحدود لتايلور من الدرجة السابعة (باللون الوردي) بالنسبة لدورة كاملة متمركزة حول أصل المَعلم.

الرسوم المتحركة لتقريب جيب التمام بواسطة متعددة الحدود لتايلور.

\cos(x)

إلى جانب متعددات الحدود الأولى لتايلور

p_{n}(x)=\sum _{k=0}^{n}(-1)^{k}{\frac {x^{2k}}{(2k)!}}

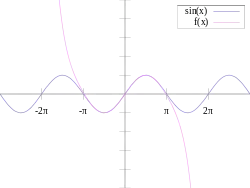
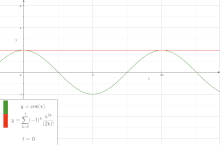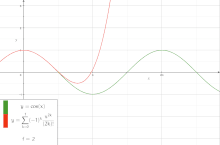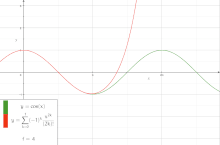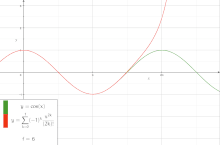
دوال مثلثية هي دوال تحليلية. يمكن تمثيل جميع الدوال المثلثية بواسطة متسلسلات لانهائية.

باستخدام متسلسلة تايلور، يمكن كتابة كل دالة مستمرة على شكل متسلسلة قوة بجوار النقطة $a$ على النحو التالي:[85]

f(x)=f(a)+{\frac {f'(a)}{1!}}(x-a)+{\frac {f''(a)}{2!}}(x-a)^{2}+{\frac {f'''(a)}{3!}}(x-a)^{3}+\cdots

حيث يرمز $n!$ إلى عاملي عدد.

عندما يكون $a =0$ ، تتحول هذه المتسلسلة إلى متسلسلة ماكلورين، رياضيا:[86]

f(x)=f(0)+{\frac {f'(0)}{1!}}x+{\frac {f''(0)}{2!}}x^{2}+{\frac {f^{(3)}(0)}{3!}}x^{3}+\cdots

ملاحظة: الزاوية x مقاسة بالتقدير الدائري في جميع السلاسل التالية.

متسلسلات ماكلورين لكل من الجيب وجيب التمام

جيب الزاوية:[87]

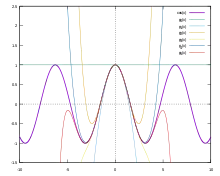
يوضح الشكل المقابل الرسم البياني لدالة الجيب إلى جانب متعدد الحدود السابع لماكلورين. قيمة دالة الجيب عند الصفر تساوي صفر، لذا فإن الحدود الزوجية لمتسلسلة القوة للجيب هي صفر. ونتيجة لذلك، فإن متسلسلة القوة للجيب ستحتوي فقط على حدود فردية.

{\begin{aligned}\sin x&=x-{\frac {x^{3}}{3!}}+{\frac {x^{5}}{5!}}-{\frac {x^{7}}{7!}}+\cdots \\[8pt]&=\sum _{n=0}^{\infty }{\frac {(-1)^{n}}{(2n+1)!}}x^{2n+1},\\[8pt]\end{aligned}}

جيب تمام الزاوية

وبالمثل، فإن الحدود الفردية لمتسلسلة جيب التمام هي صفر ، وتحتوي المتسلسلة فقط على حدود زوجية.

{\begin{aligned}\cos x&=1-{\frac {x^{2}}{2!}}+{\frac {x^{4}}{4!}}-{\frac {x^{6}}{6!}}+\cdots \\&=\sum _{n=0}^{\infty }{\frac {(-1)^{n}x^{2n}}{(2n)!}}.\end{aligned}}

نصف قطر التقارب [ملاحظة 17] لتلك المتسلسلات غير منتهية. ولذلك، يمكن أن تمدد دالتا الجيب وجيب التمام إلى دوال كاملة، والتي هي (بالتعريف) دوال ذات قيم عقدية (مركبة) وتامة الشكل على مجمل المستوي العقدي.[88]

متسلسلات القوى لباقي الدوال

الدوال المثلثية الأخرى لها مجالات خاصة، لذلك لا يمكن تحديد متسلسلة تايلور لأي قيمة. بالنسبة لدالتي الظل والقاطع اللتان هي غير معرفة عند π/2 (أو °90)، فإن مجال تعريف متسلسلاتهم هي بين -π/2 و π/2، لذا، يمكن تمثيل هاتين الدالتين بواسطة متسلسلة ماكلورين. أيضًا بالنسبة لدالتي ظل التمام وقاطع التمام اللتان هي غير معرفة عند الصفر، فإن مجال تعريف متسلسلاتهم هي بين 0 و $π$ وبين $-π$ و 0، لذلك، يمكن تمثيلهن بواسطة متسلسلة لوران، هذه الأخيرة، هي تمثيل دالة على شكل متسلسلة القوى ذات درجات سالبة (متسلسلة ذات بعض الحدود المرفوعة لِأُس سالب).[89]

بتعبير أدق، نعرف:

$U n$ ، هو عدد Up/down من الرتبة n.

$B n$ ، هو عدد بيرنولي من الرتبة n.

و $E n$ ، هو عدد أويلر من الرتبة n.

{\begin{aligned}\tan x&=\sum _{n=0}^{\infty }{\frac {U_{2n+1}x^{2n+1}}{(2n+1)!}}\\&=\sum _{n=1}^{\infty }{\frac {(-1)^{n-1}2^{2n}(2^{2n}-1)B_{2n}x^{2n-1}}{(2n)!}}=x+{\frac {1}{3}}x^{3}+{\frac {2}{15}}x^{5}+{\frac {17}{315}}x^{7}+\cdots ,\qquad {\text{for }}|x|<{\frac {\pi }{2}}\\\cot x&=\sum _{n=0}^{\infty }{\frac {(-1)^{n}2^{2n}B_{2n}x^{2n-1}}{(2n)!}}=x^{-1}-{\frac {1}{3}}x-{\frac {1}{45}}x^{3}-{\frac {2}{945}}x^{5}-\cdots ,\qquad {\text{for }}0<|x|<\pi \\\sec x&=\sum _{n=0}^{\infty }{\frac {U_{2n}x^{2n}}{(2n)!}}\\&=\sum _{n=0}^{\infty }{\frac {(-1)^{n}E_{2n}x^{2n}}{(2n)!}}=1+{\frac {1}{2}}x^{2}+{\frac {5}{24}}x^{4}+{\frac {61}{720}}x^{6}+\cdots ,\qquad {\text{for }}|x|<{\frac {\pi }{2}}\\\csc x&=\sum _{n=0}^{\infty }{\frac {(-1)^{n+1}2(2^{2n-1}-1)B_{2n}x^{2n-1}}{(2n)!}}=x^{-1}+{\frac {1}{6}}x+{\frac {7}{360}}x^{3}+{\frac {31}{15120}}x^{5}+\cdots ,\qquad {\text{for }}0<|x|<\pi \end{aligned}}

تُعرف الدوال المثلثية الأربعة الأخيرة على أنها كسور من الدوال الكاملة. ولذلك، يمكن أن تُمدّد إلى دوال جزئية الشكل، والتي هي دوال تامة الشكل في كامل المستوي العقدي، باستثناء بعض النقاط المعزولة التي تسمى الأقطاب. هنا، الأقطاب هي أعداد من الشكل ${\textstyle (2k+1){\frac {\pi }{2}}}$ بالنسبة لدالتي الظل والقاطع، أو $k\pi$ بالنسبة لدالتي ظل التمام وقاطع التمام، حيث $k$ هو عدد صحيح كيفي.[90]

يمكن أيضًا حساب علاقات الاستدعاء الذاتي لمعاملات متسلسلة تايلور لتلك الدوال. متسلسلاتهما لها نصف قطر التقارب منتهي. معاملاتهم لها تفسير توافقي: فهي تُعدّد التبديلات المتناوبة للمجموعات المنتهية.[91]

عدد الحدود في متسلسلة القوة المستخدمة لتقريب الدوال غير منتهي، ولكن في الحسابات يتم استخدام عدد محدود من تلك الحدود. يطلق على الحدود الأخرى غير المحسوبة اسم الباقي. يُعرَّف الباقي من الرتبة n لمتسلسلة بواسطة:[59]

R_{n}(x)={\frac {f^{(n+1)}(c)}{(n+1)!}}(x-a)^{n+1},a<c<x

مع زيادة قيمة x، ستكون هناك حاجة إلى المزيد من الحدود لتحقيق دقة معينة، ونتيجة لذلك، ستنخفض سرعة التقارب. بالإضافة إلى ذلك، فإن الدوال الأربعة الأخيرة لها نقاط عدم الاستمرار (نقاط عدم الإتصال)، ومتسلسلات القوى لهذه الدوال معرفة على مجال معين.

لمنع التقارب من التباطؤ والتخلص من مشكلة نقاط عدم الاستمرار، يجب علينا تقليص الزاوية قدر الإمكان قبل استخدام المتسلسلة. باستخدام متطابقات الزوايا المتتامة، يمكن تقليص الزاوية إلى $(0,{\tfrac {\pi }{4}})$ ، وباستخدام بعض المتطابقات المثلثية إلى $(0,{\tfrac {\pi }{2}})$ . بهذه الطريقة، تزداد سرعة تقارب المتسلسلة والكفاءة الحسابية.[92]

متسلسلات أخرى

هناك تمثيل متسلسلات تحليلا كسريا جزئيا، حيث يتم تجميع دوال المقلوب المزاحة فقط، بحيث تتطابق أقطاب دالة ظل التمام ودوال المقلوب:[93]

\pi \cot \pi x=\lim _{N\to \infty }\sum _{n=-N}^{N}{\frac {1}{x+n}}

يمكن إثبات هذه المتطابقة بواسطة خدعة هرغلوتز (Herglotz).[94]

الكسور المستمرة المعممة

طالع أيضًا: كسر مستمر معمم

كسر مستمر معمم هو تعميم للكسور المستمرة الاعتيادية حيث تأخذ مقاماته وبسوطه قِيَمًا حقيقية أو عقدية ما.

يمكننا كتابة الدوال الرياضية على هذا النحو:[95]

a_{0}+a_{0}a_{1}+a_{0}a_{1}a_{2}+\cdots +a_{0}a_{1}a_{2}\cdots a_{n}={\cfrac {a_{0}}{1-{\cfrac {a_{1}}{1+a_{1}-{\cfrac {a_{2}}{1+a_{2}-{\cfrac {\ddots }{\ddots {\cfrac {a_{n-1}}{1+a_{n-1}-{\cfrac {a_{n}}{1+a_{n}}}}}}}}}}}}}\,

فيما يلي الكسور المستمرة لبعض الدوال:

{\begin{aligned}\sin x={\cfrac {x}{1+{\cfrac {x^{2}}{2\cdot 3-x^{2}+{\cfrac {2\cdot 3x^{2}}{4\cdot 5-x^{2}+{\cfrac {4\cdot 5x^{2}}{6\cdot 7-x^{2}+\ddots }}}}}}}},&&&&&&&&&\cos x={\cfrac {1}{1+{\cfrac {x^{2}}{2-x^{2}+{\cfrac {2x^{2}}{3\cdot 4-x^{2}+{\cfrac {3\cdot 4x^{2}}{5\cdot 6-x^{2}+\ddots }}}}}}}}\end{aligned}}

{\begin{aligned}\tan x={\cfrac {x}{1-{\cfrac {x^{2}}{3-{\cfrac {x^{2}}{5-{\cfrac {x^{2}}{7-\dots }}}}}}}}={\cfrac {1}{{\cfrac {1}{x}}-{\cfrac {1}{{\cfrac {3}{x}}-{\cfrac {1}{{\cfrac {5}{x}}-{\cfrac {1}{{\cfrac {7}{x}}-\dots }}}}}}}},&&&&&&\cot x={\cfrac {1}{x}}-{\cfrac {x}{3-{\cfrac {x^{2}}{5-{\cfrac {x^{2}}{7-{\cfrac {x^{2}}{9-\dots }}}}}}}}\end{aligned}}

متسلسلة الجداء اللانهائي

الجداء اللانهائي التالي لدالة الجيب له أهمية كبيرة في التحليل العقدي:[96]

$\sin z=z\displaystyle \prod _{n=1}^{\infty }\left(1-{\frac {z^{2}}{n^{2}\pi ^{2}}}\right),\quad z\in \mathbb {C} .$

من هذه المتسلسلة، نستنتج أن:[96]

$\cos z=\displaystyle \prod _{n=1}^{\infty }\left(1-{\frac {z^{2}}{\left(n-{\frac {1}{2}}\right)^{2}\pi ^{2}}}\right),\quad z\in \mathbb {C} .$

باستخدام المعادلات الدالية

يمكننا أيضا تعريف الدوال المثلثية باستخدام المعادلات الدالية المختلفة.[ملاحظة 18]

مثلا،[97] الجيب وجيب التمام هما دالتان فريدتان من الدوال المستمرة التي تحقق صيغة الفرق:

\cos(x-y)=\cos x\cos y+\sin x\sin y\,

بشرط أن تكون $0<x\cos x<\sin x<x$ من أجل $0<x<1$ .

في المستوي المركب

طالع أيضًا: تحليل مركب

يمكن التعبير عن الجيب وجيب التمام لعدد مركب بدلالة الدوال نفسها والدوال الزائدية:[98]

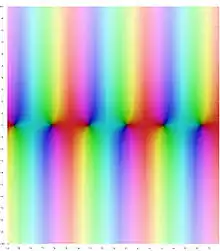
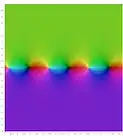
${\begin{aligned}\sin(x+iy)&=\sin x\cosh y+i\cos x\sinh y\\[5pt]\cos(x+iy)&=\cos x\cosh y-i\sin x\sinh y\end{aligned}}$

من الممكن أن نمثل بيانيا الدوال المثلثية دوالا ذات قيم عقدية (مركبة) عن طريق تمثيل بواسطة الألوان. يمكن مشاهدة العديد من الميزات الفريدة للدوال العقدية من الرسم البياني؛ على سبيل المثال، يمكن اعتبار دالتي الجيب وجيب التمام أنهما غير منتهية عندما يصبح الجزء التخيلي لـ z أكبر (لأن اللون الأبيض يمثل اللانهاية)، وحقيقة أن الدوال تحتوي على أصفار أو أقطاب بسيطة تتضح من حقيقة أن الألوان تدور حول كل صفر أو قطب مرة واحدة بالضبط. إن مقارنة هذه التمثيلات البيانية (بواسطة الألوان) مع تلك التمثيلات الخاصة بالدوال الزائدية توضح العلاقات بينهما.[99]

تمثيل الدوال على المستوى العقدي:


$\sin z\,$	$\cos z\,$	$\tan z\,$	$\cot z\,$	$\sec z\,$	$\csc z\,$	التمثيل البياني لـ $z = x + iy$ التي استخدمت في التمثيلات البيانية.

حيث تمثل عمدة عدد مركب بالألوان، ومعياره بوسائل أخرى، مثل السطوع أو الاشباع اللوني.

الخصائص

زوجية وفردية

مقالة مفصلة: دوال زوجية وفردية

الدوال الزوجية والدوال الفردية هي دوال تحقق شرطا معينا يتعلق بالتناظر.

جيب التمام والقاطع دالتان زوجيتان، أما الدوال الأخرى فهي دوال فردية، بتعبير آخر:

${\begin{aligned}\sin(-x)&=-\sin x\\\cos(-x)&=\cos x\\\tan(-x)&=-\tan x\\\cot(-x)&=-\cot x\\\csc(-x)&=-\csc x\\\sec(-x)&=\sec x.\end{aligned}}$

دورية

مقالة مفصلة: دالة دورية

الدوال المثلثية كلها دوالٌ دوريةٌ أصغر دورة لها هي $2 π$ . باستثناء الظل وظل التمام، التي أصغر دورة لها هي $π$ ، بتعبير آخر، من أجل عدد صحيح $k$ ، لدينا:

${\begin{aligned}\sin(x+2k\pi )&=\sin x\\\cos(x+2k\pi )&=\cos x\\\tan(x+k\pi )&=\tan x\\\cot(x+k\pi )&=\cot x\\\csc(x+2k\pi )&=\csc x\\\sec(x+2k\pi )&=\sec x.\end{aligned}}$

في تحويل فورييه والمعادلات الموجية، تستخدم خاصية دورية الدوال المثلثية لحل المعادلات التفاضلية.[59]

استمرارية (اتصال)

إن الجيب وجيب التمام هما دالتان مستمرتان دومٌا وقابلة للإشتقاق ويتضح ذلك بوضوح من خلال التعريف بواسطة المثلث القائم والتعريف بواسطة دائرة الوحدة. إن الدوال الأخرى، التي مقامهما هي دالة الجيب أو جيب التمام، ليست دائمًا مستمرة. لأن قيمة كل من دالة الجيب وجيب التمام في بعض الأماكن تساوي الصفر. نقاط عدم الاستمرار للدوال المثلثية هي كالتالي (حيث k هو عدد صحيح كيفي):

الظل والقاطع: ${\pi \over 2}+k\pi$
ظل التمام وقاطع التمام: $k\pi$

تعامد

تعتبر دالتا الجيب وجيب التمام دالتان متعامدتان (Orthogonals)، أي:[ملاحظة 19]

$\int _{0}^{2\pi }\cos n\theta \sin m\theta \,d\theta =0.$

${\frac {1}{\pi }}\int _{0}^{2\pi }\cos n\theta \cos m\theta \,d\theta =\left\{{\begin{array}{l l}0&\quad n\neq m\\1&\quad n=m\end{array}}\right.$

$\int _{0}^{2\pi }\sin m\theta \sin n\theta \,d\theta =0\quad (n\neq m).$

تستخدم هذه الخصائص لحساب معاملات متسلسلة فورييه.[100][101]

تحويلا لابلاس وفورييه

تحويل لابلاس هو أحد طرق حل المعادلات التفاضلية. تحويلات لابلاس لدالتي الجيب وجيب التمام هي كما يلي:[ملاحظة 20][102]

تحويل الجيب:

{\mathcal {L}}\{\sin(at)\}={\frac {a}{s^{2}+a^{2}}}

تحويل جيب التمام:

{\mathcal {L}}\{\cos(at)\}={\frac {s}{s^{2}+a^{2}}}

تحويلات فورييه لدالتي الجيب وجيب التمام هي كما يلي:[ملاحظة 21][103]

الجيب:

{\mathcal {F}}\{\sin(at)\}={\frac {\displaystyle \delta \left(\omega -{\frac {a}{2\pi }}\right)-\delta \left(\omega +{\frac {a}{2\pi }}\right)}{2i}}

جيب التمام:

{\mathcal {F}}\{\cos(at)\}={\frac {\delta \left(\omega -{\frac {a}{2\pi }}\right)+\delta \left(\omega +{\frac {a}{2\pi }}\right)}{2}}

دالة ذاتية

إن دالتا الجيب وجيب التمام هما دالتان ذاتيتان (Eigenfunctions) لمؤثر لابلاس. على سبيل المثال، إذا كان : $\Delta =\nabla ^{2}$ يمثل مؤثر لابلاسي أحادي البعد، فإن دالتا الجيب وجيب التمام تحقق : $\nabla ^{2}f=\lambda f$ ، حيث $\lambda$ هي قيمة ذاتية؛ يمكن التحقق من هذه المساواة انطلاقا من التعريف بواسطة المعادلة التفاضلية للدالتين.[104]

حساب القيم

مقالة مفصلة: جداول مثلثية

حساب القيم الدقيقة للدوال المثلثية يدوياً أمر صعب ومعقد، لكن في العصرِ الحديثِ، زالَت تعقيداته بسبب توفر أجهزة الحاسوب والآلات الحاسبة، التي تمكن بسهولة الحصول على القيمة الدقيقة لأي زاوية. بالنسبةِ لبعضِ الزوايا، فيمكن الحصول على القيم الجبرية الدقيقة لدولِّها المثلثية دون اللجوء إلى حساباتٍ بالأجهزة، وتُسمّى هذه الزوايا: الزوايا الخاصة. على سبيل المثال، قيمُ الدوال المثلثية لجميع الزوايا من مضاعفات العدد 3 دقيقة. تُحسَبُ النسب المثلثية للزاوية 3° بتطبيق الفرق بين زاويتين ذات القيم 18° و15° (3 = 15 - 18). وتُحسَبُ النسب المثلثية للزاوية 18° باستخدام خواص ونِسَب الخماسي المنتظم.

لحساب قيمة دالة لأي زاوية، يجب على المرء أولاً تقليص مجال الزاوية (على سبيل المثال، من الصفر إلى $π / 2$ ). يتم ذلك باستخدام كل من خاصية دورية وتناظر الدوال المثلثية.[105]

قبل الحواسيب، حصل الناس بشكل عام على قيمة الدوال المثلثية من خلال استيفاء الجداول المثلثية. هذه الجداول لها تاريخ طويل في علم المثلثات. عادة ما يتم الحصول على القيم في الجداول عن طريق استخدام متطابقات نصف الزاوية وضعف الزاوية، على التوالي، بدءاً بقيمة معروفة (مثل $sin (π / 2) = 1$ ).[41]

تستخدم الحواسيب والحاسبات الحديثة مجموعةً متنوعةً من التقنياتِ لتوفير قيم الدوال المثلثية عند الطلب للزوايا الأخرى. تتمثل إحدى الطرق الشائعة، خاصةً في المعالِجات الراقية (Higher-end Processors) ذات وحدات الفاصلة العائمة، في جمع بين تقريب بواسطة كثير الحدود أو بواسطة الدوال الكسرية (مثل تقريب تشيبيشيف، تقريب بادي، وعادةً ما يتعلق بالدقة العليا أو المتغيرة، متسلسلات تايلور ومتسلسلة لوران) وتقليص المدى (Range reduction) والبحث في الجدول—تبحث (الخوارزميات) أولاً في جدول صغير عن أقرب زاوية، ثم تستخدم كثير الحدود لحساب التصحيح.[106][107] على الأجهزة الأكثر بساطة التي تفتقر إلى مضاعف العتاد، توجد خوارزمية تسمى CORDIC عالية الكفاءة، لأنها تَستَخدِم الإزاحات والإضافة والطرح فقط.[108]

بالنسبة لحسابات عالية الدقة، عندما يصبح تقارب المتسلسلة بطيئًا للغاية، يمكن تقريب الدوال المثلثية بواسطة المتوسط الحسابي الهندسي، الذي يقارب في حد ذاته الدالة المثلثية بواسطة تكامل اهليلجي (المركب).[109]

متطابقات أساسية و مبرهنات

طالع أيضًا: قائمة المطابقات المثلثية

هناك عدد من المتطابقات تربط الدوال المثلثية بعضها ببعض. يحتوي هذا القسم على المتطابقات الأساسية والمبرهنات، لمزيد من المتطابقات، طالع قائمة المطابقات المثلثية. يمكن إثبات هذه المتطابقات هندسيا من التعريف باستعمال دائرة الوحدة أو التعريف باستعمال المثلث القائم (على الرغم من أنه بالنسبة للتعاريف الأخيرة، يجب توخي الحذر للزوايا التي لا تنتمي إلى هذا المجال $[0 , π/2]$ ). بالنسبة إلى البراهين غير الهندسية التي تستخدم فقط أدوات حساب التفاضل والتكامل، يمكننا استخدام المعادلات التفاضلية مباشرة. يمكننا أيضا استخدام متطابقة أويلر للتعبير عن جميع الدوال المثلثية بدلالة الدالة الأسية العقدية واستخدام خصائص الدالة الأسية.

متطابقة فيثاغورس

مقالة مفصلة: متطابقة فيثاغورس المثلثية

تنص هذه المتطابقة على أن مجموع مربع جيب زاوية ما، لتكن $x$ ، مع مربع الجيب التمام لنفس الزاوية يساوي الواحد، ويُعبر عنها رياضياً بالعلاقة التالية:[60]

\sin ^{2}x+\cos ^{2}x=1,\,

يجب الانتباه إلى أن الترميز sin² x + cos² x يكافئ sin x)² + (cos x)²).

متطابقات مجموع وفرق زاويتين

تسمح صيغ الفرع والمجموع بتوسيع الجيب وجيب التمام والظل لمجموع أو فرق زاويتين بدلالة جيب وجيب تمام وظل الزوايا نفسها.

المجموع

ويُحسب كما يأتي:[67]

${\begin{aligned}\sin \left(x+y\right)&=\sin x\cos y+\cos x\sin y,\\\cos \left(x+y\right)&=\cos x\cos y-\sin x\sin y,\\\tan(x+y)&={\frac {\tan x+\tan y}{1-\tan x\tan y}}.\end{aligned}}$

الفرق

ويُحسب كما يأتي:[67]

${\begin{aligned}\sin \left(x-y\right)&=\sin x\cos y-\cos x\sin y,\\\cos \left(x-y\right)&=\cos x\cos y+\sin x\sin y,\\\tan(x-y)&={\frac {\tan x-\tan y}{1+\tan x\tan y}}.\end{aligned}}$

متطابقات ضعف الزاوية

عندما تكون الزاويتان متساويتان، فإن صيغ المجموع تقلص إلى معادلات أبسط تعرف باسم متطابقات ضعف الزاوية.[67]

{\begin{aligned}\sin 2x&=2\sin x\cos x={\frac {2\tan x}{1+\tan ^{2}x}},\\\cos 2x&=\cos ^{2}x-\sin ^{2}x=2\cos ^{2}x-1=1-2\sin ^{2}x={\frac {1-\tan ^{2}x}{1+\tan ^{2}x}},\\\tan 2x&={\frac {2\tan x}{1-\tan ^{2}x}}.\end{aligned}}

يمكن استخدام هذه المتطابقات لاشتقاق متطابقات التحويل من المجموع إلى الجداء.

بوضع $\theta =2x$ و $t=\tan x,$ هذا يسمح بالتعبير عن جميع الدوال المثلثية لـ $\theta$ كدالة كسرية لـ ${\textstyle t=\tan {\frac {\theta }{2}}}$

${\begin{aligned}\sin \theta &={\frac {2t}{1+t^{2}}},\\\cos \theta &={\frac {1-t^{2}}{1+t^{2}}},\\\tan \theta &={\frac {2t}{1-t^{2}}}.\end{aligned}}$

بالإضافة إلى $d\theta ={\frac {2}{1+t^{2}}}\,dt$

هذا هو التعويض بظل نصف الزاوية (ويسمى أيضا تعويض فايرشتراس)، الذي يسمح بتقليص حساب التكاملات والمشتقات العكسية للدوال المثلثية إلى دوال كسرية.[110]

متطابقات ثلاثية الزاوية

ويُحسب كما يأتي:[111]

\sin(3\theta )=3\sin \theta -4\sin ^{3}\theta =4\sin \theta \sin({\frac {\pi }{3}}-\theta )\sin({\frac {\pi }{3}}+\theta )

\cos(3\theta )=4\cos ^{3}\theta -3\cos \theta =4\cos \theta \cos({\frac {\pi }{3}}-\theta )\cos({\frac {\pi }{3}}+\theta )

\tan(3\theta )={\frac {3\tan \theta -\tan ^{3}\theta }{1-3\tan ^{2}\theta }}=\tan \theta \tan({\frac {\pi }{3}}-\theta )\tan({\frac {\pi }{3}}+\theta )

متطابقات نصف الزاوية

ويُحسب كما يأتي:[112]

\sin {\frac {\theta }{2}}=\pm {\sqrt {\frac {1-\cos \theta }{2}}}

\cos {\frac {\theta }{2}}=\pm {\sqrt {\frac {1+\cos \theta }{2}}}

\tan {\frac {\theta }{2}}=\pm {\sqrt {\frac {1-\cos \theta }{1+\cos \theta }}}={\frac {\sin \theta }{1+\cos \theta }}={\frac {1-\cos \theta }{\sin \theta }}=\csc \theta -\cot \theta

قانون الجيب

ليكن ABC مثلث، وa وb وc أضلاعه، ينص قانون الجيب على ما يلي:

{\frac {\sin A}{a}}={\frac {\sin B}{b}}={\frac {\sin C}{c}}={\frac {2\Delta }{abc}}

حيث تشير

Δ

إلى مساحة المثلث، أو بشكل مكافئ:

{\frac {a}{\sin A}}={\frac {b}{\sin B}}={\frac {c}{\sin C}}=2R,

حيث يشير

R

إلى نصف قطر الدائرة المحيطة بالمثلث.[67]

يمكن إثبات ذلك بتقسيم المثلث إلى مثلثين قائمين وباستخدام التعريف الوارد أعلاه للجيب. قانون الجيب مفيد في حساب أطوال الأضلاع المجهولة في مثلث إذا كانت هناك زاويتان وضلع واحد معلومتان. هذا هو الموقف الشائع الذي يحدث في التثليث، وهي تقنية لتحديد مسافات غير معروفة عن طريق قياس زاويتين ومسافة مغلقة يمكن الوصول إليها.

تمثيل المثلث الكروي ABC

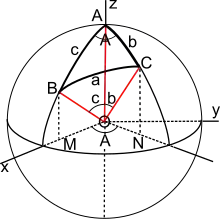
في حالة المثلثات الكروية، ينص القانون على ما يلي:[31]

{\frac {\sin A}{\sin a}}={\frac {\sin B}{\sin b}}={\frac {\sin C}{\sin c}}

حيث a و b و c هن أضلاع المثلث الواقع في سطح الكرة؛ و A و B و C هن الزوايا المقابلة.[ملاحظة 22]

قانون جيب التمام

طريقة الكاشي لبرهنة قانون جيب التمام بالنسبة للمثلثات الحادة (باستخدام مثلث حاد محاط بثلاث مربعات). حيث أن المستطيلان الأخضران متقايسان والمستطيلان الأحمران أيضًا متقايسان، يمكن إثبات م.خ التقايس بإثبات تقايس المثلثات JAE و JAB ، و JAB و CAM ، و CAM و FAM بتحريك أحد الرؤوس بالتوازي مع القاعدة وأحدهما بالدوران على أحد زوايا المربعات، ويمكن الإثبات بطريقة مشابهة، المستطيلان الأحمران (طالع الصورة المتحركة)؛ ويمكن إثبات أن المستطيلان الأزرقان متقايسان ومساحة أحدهما يساوي

CA \times CB \times cos C

بمعرفة أن

CE = CB cos C

و

CD = CA cos C

. يمكن إثبات بالنسبة للمثلثات المنفرجة بطريقة مشابهة.[113]

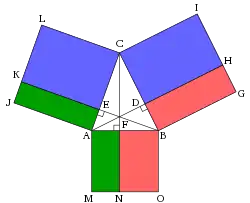
يعتبر قانون جيب التمام تعميمًا لمبرهنة فيثاغورس على جميع أنواع المثلثات المستوية. ويسمى أيضا مبرهنة الكاشي.[114]

c^{2}=a^{2}+b^{2}-2ab\cos C

وقد تكتب هاته الصيغة كما يلي:

\cos C={\frac {a^{2}+b^{2}-c^{2}}{2ab}}

حيث C هي الزاوية المقابلة للضلع

c

.

يمكن إثبات هذه المبرهنة بتقسيم المثلث إلى مثلثين قائمين وباستخدام مبرهنة فيثاغورس، أو باستخدام طريقة الكاشي كما هي موضحة على اليسار.[67]

يمكن استخدام قانون جيب التمام لحساب طول ضلع المثلث إذا كان الضلعان والزاوية بينهما معلومة. يمكن أيضًا استخدامه لإيجاد جيب تمام لأي زاوية إذا كانت أطوال كل الأضلاع معلومة.

في حالة المثلثات الكروية، ينص القانون على ما يلي:[115][116]

\cos c=\cos a\cos b+\sin a\sin b\cos C\,

حيث $a$ و $b$ و $c$ هي الأقواس الثلاثة للمثلث الكروي (والتي يطلق عليها مجازًا أضلاع وتسمى أحيانًا بجوانب المثلث الكروي) وتقاس بالدرجات القوسية أي بقيمة الزاوية المركزية المقابلة لكل منها داخل الكرة، حيث تحول بعد ذلك إلى وحدات الطول العادية بالضرب في قيمة الدرجة القوسية والتي تساوي محيط الكرة/360 ما يعادل ط × نصف قطر الكرة/180 والرمز ط هنا أو $π$ في اللاتينية؛ والزاوية $C$ هي الزاوية المقابلة للقوس $c$ .

ويمكن اشتقاق المعادلة التالية مِن العلاقة السابقة لإيجاد قيمة الزاوية $C$ المقابلة للقوس $c$ في المثلث الكروي عندما تكون مجهولة وبقية الأطوال الثلاثة لأقواس المثلث $a$ و $b$ و $c$ معلومة:

$\cos C\ ={\frac {\cos c-\cos a\cos b}{\sin a\sin b}}$

وهناك صورة أخرى للمعادلة حيث تكون قيم الزوايا الثلاث $A$ و $B$ و $C$ معلومة لنحصل على قيمة قوس مجهول في المثلث الكُرويّ وليكن القوس $c$ كما يلي:[117]

$\cos c\ ={\frac {\cos C+\cos A\cos B}{\sin A\sin B}}$

ومنها يمكن حساب قيمة زاوية مجهولة بمعلومية طول القوس المقابل لها ومعلومية قيمتي الزاويتين الأخرتين بالمثلث الكروي هكذا:

$\cos C=\sin A\sin B\cos c\,-\cos A\cos B$

قانون الظل

مقالة مفصلة: قانون الظل

ليكن ABC مثلث، تنص الأشكال الاربعة لقانون الظل على ما يلي:[118]

{\frac {\tan {\frac {A-B}{2}}}{\tan {\frac {A+B}{2}}}}={\frac {a-b}{a+b}}\,;\qquad {\frac {\tan {\frac {A-C}{2}}}{\tan {\frac {A+C}{2}}}}={\frac {a-c}{a+c}}\,;\qquad {\frac {\tan {\frac {B-C}{2}}}{\tan {\frac {B+C}{2}}}}={\frac {b-c}{b+c}}.

حيث a=BC وb=AC وc=AB.

يمكن إثبات هذه المبرهنة باستخدام قانون الجيب والمتطابقات المثلثية.

أما بالنسبة للمثلثات الكروية، ينص القانون على ما يلي:[ملاحظة 22][119]

{\frac {\tan \left({\dfrac {A-B}{2}}\right)}{\tan \left({\dfrac {A+B}{2}}\right)}}={\frac {\tan \left({\dfrac {a-b}{2}}\right)}{\tan \left({\dfrac {a+b}{2}}\right)}}.

قانون ظل التمام

مقالة مفصلة: قانون ظل التمام

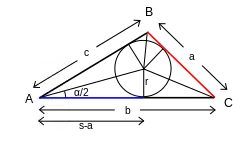
ليكن ABC مثلث، وa وb وc أضلاعه (حيث a=BC وb=AC وc=AB)، إذا كان:

r=\zeta ={\sqrt {{\frac {1}{s}}(s-a)(s-b)(s-c)}}~

(نصف قطر الدائرة الداخلية للمثلث)

و

s={\frac {a+b+c}{2}}~

(نصف محيط المثلث)،

ثم كل ما يلي يشكل قانون ظل التمام:[118]

\cot {\frac {A}{2}}={\frac {s-a}{\zeta }}~;\qquad \cot {\frac {B}{2}}={\frac {s-b}{\zeta }}~;\qquad \cot {\frac {C}{2}}={\frac {s-c}{\zeta }}~.

نستنتج أن:

{\frac {\cot {\dfrac {A}{2}}}{s-a}}={\frac {\cot {\dfrac {B}{2}}}{s-b}}={\frac {\cot {\dfrac {C}{2}}}{s-c}}={\frac {1}{\zeta }}~.

مبرهنة الساندويتش

طالع أيضًا: مبرهنة الساندويتش

تساعد هذه المبرهنة في حساب النهايات الصعبة ومشتقات الدوال المثلثية. هذه المتباينة الصالحة فقط عند المجال $-{\pi \over 2}<\theta <{\pi \over 2}$ ، هي كما يلي:[120]

\cos \theta <{\frac {\sin \theta }{\theta }}<1

تمكننا هذه المتباينة من حساب النهاية التالية:[121] $\lim _{x\to 0}{\frac {\sin x}{x}}$ . تفيد هذه النهاية في حساب مشتقات الدوال المثلثية، طالع تفاضل الدوال المثلثية.

المتباينات المشابهة هي كما يلي:[122]

${\frac {2}{\pi }}x\leq \sin x\leq x\qquad 0\leq x\leq {\frac {\pi }{2}}.$

$x\leq \tan x\qquad 0\leq x\leq {\frac {\pi }{2}}.$

$x<{\frac {\sin(\pi x)}{x(1-x)}}\leq 4\qquad 0\leq x\leq 1.$

مبرهنة بطليموس

مقالة مفصلة: مبرهنة بطليموس

مبرهنة بطليموس هي علاقة بين الأضلاع الأربعة وقطرا الرباعي الدائري (رباعي محاط بدائرة تشمل جميع رؤوسه).

ليكن ABCD رباعي دائري، إذا كان $θ 1 + θ 2 + θ 3 + θ 4 =180°$ ، فإن:[123]

{\begin{aligned}\sin(\theta _{1}+\theta _{2})\sin(\theta _{2}+\theta _{3})&=\sin(\theta _{2}+\theta _{3})\sin(\theta _{3}+\theta _{4})&{\text{(trivial)}}\\&=\sin(\theta _{3}+\theta _{4})\sin(\theta _{4}+\theta _{1})&{\text{(trivial)}}\\&=\sin(\theta _{4}+\theta _{1})\sin(\theta _{1}+\theta _{2})&{\text{(trivial)}}\\&=\sin \theta _{1}\sin \theta _{3}+\sin \theta _{2}\sin \theta _{4}.&{\text{(significant)}}\end{aligned}}

صيغة مولفيده

مقالة مفصلة: صيغة مولفيده

لتكن a و b و c أطوال أضلاع للمثلث، و α و β و γ الزوايا المقابلة لتلك الأضلاع الثلاثة على التوالي. تنص صيغة مولفيده على ما يلي:[124]

{\frac {a+b}{c}}={\frac {\cos \left({\frac {\alpha -\beta }{2}}\right)}{\sin \left({\frac {\gamma }{2}}\right)}}

{\frac {a-b}{c}}={\frac {\sin \left({\frac {\alpha -\beta }{2}}\right)}{\cos \left({\frac {\gamma }{2}}\right)}}

قانون موري

ينص هذا القانون الرياضي على أن جداء جيوب التمام لكل من $20°$ و $40°$ و $80°$ يساوي 1/8، بتعبير رياضي:

\cos(20^{\circ })\cdot \cos(40^{\circ })\cdot \cos(80^{\circ })={\frac {1}{8}}.

وهي حالة خاصة للمتطابقة العامة:

2^{n}\cdot \prod _{k=0}^{n-1}\cos(2^{k}\alpha )={\frac {\sin(2^{n}\alpha )}{\sin(\alpha )}}

مع $n=3$ و $\alpha =20^{\circ }$ .

هذه المتطابقة تثير الفضول، لأن، عند تعويض n و α للحد الثاني بتلك القيم، يحصل المرء على أن:

{\frac {\sin(160^{\circ })}{\sin(20^{\circ })}}={\frac {\sin(180^{\circ }-20^{\circ })}{\sin(20^{\circ })}}=1,

بما أن:

\sin(180^{\circ }-x)=\sin(x).

هناك متطابقة مشابهة لهذه المتطابقة، وهي متعلقة بدالة الجيب:

\sin(20^{\circ })\cdot \sin(40^{\circ })\cdot \sin(80^{\circ })={\frac {\sqrt {3}}{8}}.

زيادة على ذلك، عند تقسيم المتطابقة الثانية على الأولى، تنتج متطابقة أخرى:[125]

\tan(20^{\circ })\cdot \tan(40^{\circ })\cdot \tan(80^{\circ })={\sqrt {3}}=\tan(60^{\circ }).

الدوال العكسية

مقالة مفصلة: دوال مثلثية عكسية

الدوال المثلثية دورية، وبذلك، هي ليست متباينة، وبالتالي ليس لديها دالة عكسية. ومع ذلك، في كل مجال تكون فيه الدالة المثلثية رتيبة، يمكن للمرء تحديد دالة عكسية، بهذه الطريقة، تعرّف الدوال المثلثية العكسية كدوال متعددة القيم. لتعريف دالة عكسية حقيقية، يصير من الضروري تقليص مجال تعريفها إلى مجال تكون فيه الدالة رتيبة، حتى تكون الدوال المثلثية دوالا تقابلية. يعطى الاختيار الشائع لهذا المجال الذي يطلق عليه اسم "مجموعة القيم الرئيسية" في الجدول التالي. عادة ما يرمز إلى الدوال المثلثية العكسية بالبادئة "arc" قبل اسم أو اختصار الدالة.[126]

يوضح الجدول الآتي قائمة الدوال المثلثية العكسية مع ابراز كل من مجال تعريفهن ومشتقتهن.

الدالة[3]	اسمها بالإنجليزية[3]	الترميز[126]	التعريف	مجال التعريف[67]	المجال المقابل (مجموعة القيم الرئيسية)[67]	المشتقة[67]
قوس الجيب	Arcsine	$\arcsin x=y\,$	$\sin y=x\,$	$-1\leq x\leq 1\,$	$-{\frac {\pi }{2}}\leq y\leq {\frac {\pi }{2}}\,$	${\frac {1}{\sqrt {1-x^{2}}}}$
قوس جيب التمام	Arccosine	$\arccos x=y\,$	$\cos y=x\,$	$-1\leq x\leq 1\,$	$0\leq y\leq \pi \,$	$-{\frac {1}{\sqrt {1-x^{2}}}}$
قوس الظل	Arctangent	$\arctan x=y\,$	$\tan y=x\,$	جميع الاعداد الحقيقية	$-{\frac {\pi }{2}}<y<{\frac {\pi }{2}}\,$	${\frac {1}{1+x^{2}}}$
قوس قاطع التمام	Arccosecant	$\operatorname {arccsc} x=y\,$	$\csc y=x\,$	$x\leq -1$ أو $x\geq 1$	$-{\frac {\pi }{2}}\leq y\leq {\frac {\pi }{2}},y\neq 0\,$	${\frac {-1}{\|x\|\,{\sqrt {x^{2}-1}}}}$
قوس القاطع	Arcsecant	$\operatorname {arcsec} x=y\,$	$\sec y=x\,$	$x\leq -1$ أو $x\geq 1$	$0\leq y\leq \pi ,y\neq {\frac {\pi }{2}}\,$	${\frac {1}{\|x\|\,{\sqrt {x^{2}-1}}}}$
قوس ظل التمام	Arccotangent	$\operatorname {arccot} x=y\,$	$\cot y=x\,$	جميع الاعداد الحقيقية	$0<y<\pi \,$	$-{\frac {1}{1+x^{2}}}$

غالبًا ما تستخدم الترميزات $sin -1$ و $cos -1$ ... إلخ لـ $arcsin$ و $arccos$ ،... وهكذا. عند استخدام هذا الترميز، قد يؤدي هذا إلى الالتباس بين الدوال العكسية والمعاكيس الضربية.[126]

يمنع الترميز بالبادئة "arc" مثل هذا الالتباس، على الرغم من أنه يمكن الخلط بين "arcsec" لـ arcsecant و لـ "arcsecond"(التي تعني "ثانية القوس").[126]

يُمكن للدوال المثلثية العكسية أن تعرف بواسطة المتسلسلات تماما كما هو الحال بالنسبة للدوال المثلثية. على سبيل المثال،

\arcsin z=z+\left({\frac {1}{2}}\right){\frac {z^{3}}{3}}+\left({\frac {1\cdot 3}{2\cdot 4}}\right){\frac {z^{5}}{5}}+\left({\frac {1\cdot 3\cdot 5}{2\cdot 4\cdot 6}}\right){\frac {z^{7}}{7}}+\cdots \,.

يمكن أيضًا التعبير عنها بدلالة اللوغاريتمات العقدية.[127] طالع دوال مثلثية عكسية لمزيد من التفاصيل.

الدوال الزائدية

مقالة مفصلة: دوال زائدية

صورة متحركة للدوال المثلثية (الدائرية) والدوال الزائدية. باللون الأحمر، منحنى معادلته x² + y² = 1 (دائرة الوحدة)، وبالأزرق x² - y² = 1 (القطع الزائد)، مع النقاط (cos(θ),sin(θ)) و (1,tan(θ)) باللون الأحمر و (cosh(θ),sinh(θ)) و (1,tanh(θ)) باللون الأزرق.

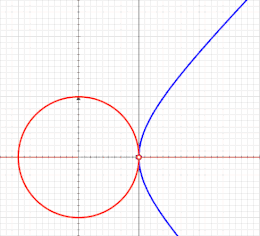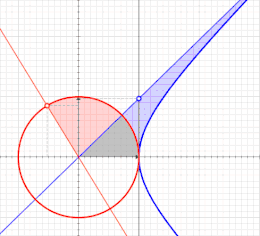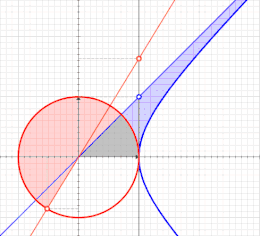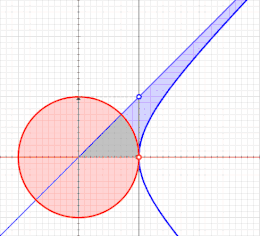
الدوال الزائدية هي تلك الدوال التي تشبه الدوال المثلثية لكنها معرفة بواسطة القطع الزائد بدلاً من الدائرة: تمامًا كما تشكل النقاط $(cos t, sin t)$ دائرة ذات نصف قطر يساوي الواحد، تشكل النقاط $(cosh t, sinh t)$ النصف الأيمن للقطع الزائد.[128]

الدوال الزائدية هي:


الدالة[3]	الترميز[129]	التعريف[129]	تعبير بدلالة الدوال المثلثية [ملاحظة 23]
الجيب الزائدي	$\sinh x$	${\frac {e^{x}-e^{-x}}{2}}$	$-i\sin ix$
جيب التمام الزائدي	$\cosh x$	${\frac {e^{x}+e^{-x}}{2}}$	$\cos ix$
الظل الزائدي	$\tanh x$	${\frac {\sinh x}{\cosh x}}={\frac {e^{x}-e^{-x}}{e^{x}+e^{-x}}}$	$-i\tan ix$
ظل التمام الزائدي	$\coth x$	${\frac {\cosh x}{\sinh x}}={\frac {e^{x}+e^{-x}}{e^{x}-e^{-x}}}$	$i\cot ix$
القاطع الزائدي	$\operatorname {sech} x$	${\frac {1}{\cosh x}}={\frac {2}{e^{x}+e^{-x}}}$	$\sec {ix}$
قاطع التمام الزائدي	$\operatorname {csch} x$	${\frac {1}{\sinh x}}={\frac {2}{e^{x}-e^{-x}}}$	$i\csc ix$

يعتمد كلا النوعين على عُمدة (Argument)، إما زاوية دائرية أو زاوية زائدية.

بما أن مساحة القطاع الدائري الذي نصف قطره $r$ وزاويته $u$ هي ${\frac {1}{2}}r^{2}u$ ، فسوف تكون مساوية لـ u عندما تكون $r = \sqrt2$ . في الرسم البياني، تكون الدائرة مماسية على القطع الزائد الذي معادلته $xy = 1$ عند النقطة (1,1). يمثل القطاع البرتقالي مساحة ومقدار الزاوية الدائرية. وبالمثل، تمثل القطاعان الأصفر والأحمر معًا مساحة ومقدار الزاوية الزائدية.

سيقان المثلثين القائمين اللذين وتراهما هما عبارة عن شعاع محدد للزوايا يبلغ طولهما 2√ مرة الدوال الدائرية والزائدية.[128]

في حالة القطع الزائد الذي معادلته $x 2 - y 2 =1$ ، مقدار الزاوية الزائدية هو ضعف المساحة الزرقاء المحددة بالشعاع ومحور السينات والقطع الزائد (انظر الصورة (8))، تماما كما يكون مقدار الزاوية الدائرية هو ضعف المساحة الزرقاء للدائرة التي معادلتها $x 2 + y 2 =1$ (انظر الصورة (9)).[128]

في المتطابقات الزائدية، هناك تشابه كبير بينها وبين المتطابقات المثلثية، بعض الأمثلة على ذلك:[128]

\sinh(x+y)=\sinh x\cosh y+\cosh x\sinh y

\cosh ^{2}x-\sinh ^{2}x=1

\cosh 2x=\cosh ^{2}x+\sinh ^{2}x

e^{x}=\cosh x+\sinh x

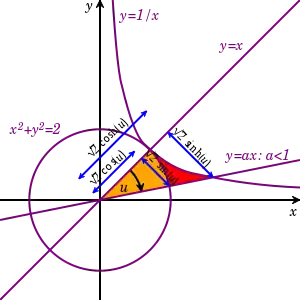(7) الدائرة والقطع الزائد متلامسان عند النقطة (1,1) تعرضان هندسة الدوال الدائرية بدلالة مقدار الزاوية u، والدوال الزائدية اعتمادًا على مقدار الزاوية u.
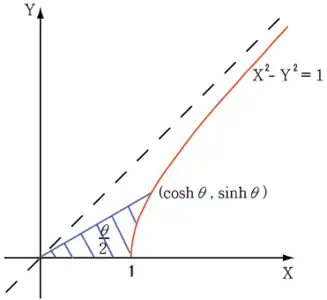(8)
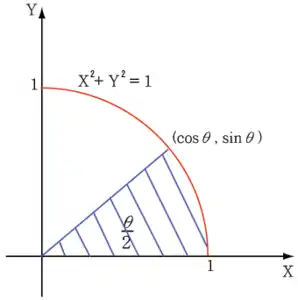(9)

علاقة الدوال المثلثية بالدوال الخاصة

يمكن كتابة بعض الدوال الخاصة بدلالة مجموعة من الدوال بما في ذلك الدوال المثلثية.

دالة بيسل من الرتبة 1/2: دالة بيسل التي هي عبارة عن متسلسلة القوى، هي حل للمعادلة التفاضلية من الدرجة الثانية التالية:

x^{2}y''+xy'+(x^{2}-a^{2})y=0

حيث يمثل $a$ الرتبة. يمكن كتابة أحد الحالات الخاصة لدالة بيسل ( $a = 1/2$ ) كدوال مثلثية على النحو التالي:[130]

J_{1/2}={\sqrt {\frac {2}{\pi x}}}\sin x

J_{-1/2}={\sqrt {\frac {2}{\pi x}}}\cos x

متعدد الحدود لشيبيشيف: هو الحل للمعادلة التفاضلية من الدرجة الثانية التالية:

(1-x^{2})y''-xy'+n^{2}y=0

حيث تمثل n رتبتها.

يمكن كتابة متعدد الحدود لتشيبيشيف من الرتبة n بدلالة الدوال المثلثية:[131]

T_{n}=\cos(n\arccos x)

تطبيقات

حساب المتجهات

في الرياضيات والفيزياء، تُستخدم المتجهات[ملاحظة 24] (التي لها مقدار واتجاه) لتمثيل كمية متجهة وبالاخص في الفيزياء مثل تمثيل القوة والسرعة. تستخدم بعض حسابات المتجهات دوال مثلثية. على سبيل المثال، يمكن حساب الجداء القياسي [ملاحظة 25]لمتجهين x وy بواسطة قانون جيب التمام:[132]

{\vec {x}}\cdot {\vec {y}}=\cos \left(\angle ({\vec {x}},{\vec {y}})\right)\ \cdot \parallel \!\!{\vec {x}}\!\!\parallel \cdot \parallel \!\!{\vec {y}}\parallel

يمكن أيضًا استخدام المعادلة التالية لحساب مقدار الضرب المتجهي:[ملاحظة 26]

\parallel {\vec {x}}\times {\vec {y}}\!\!\parallel =\sin \left(\angle ({\vec {x}},{\vec {y}})\right)\ \cdot \parallel \!\!{\vec {x}}\!\!\parallel \cdot \parallel \!\!{\vec {y}}\parallel

الإحداثيات القطبية، والأسطوانية والكروية

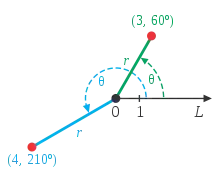
تمثيل نقطتين في نظام الإحداثيات القطبية

الدوال المثلثية هي الأساس لتحديد نظام الإحداثيات القطبية الذي يكون فعالا في تبسيط العديد من المشكلات الرياضية والفيزيائية، بما في ذلك بعض التكاملات. في نظام الإحداثيات هذا، بدلاً من إحداثيات x وy لنقطة (المستخدمة في نظام الإحداثيات الديكارتية)، بُعدها عن المركز والزاوية المحصورة بين الخط الذي يربطها بالمركز والخط الأفقي (r , θ) فهي تعتبر إحداثيات النقطة.[59] تحويل الإحداثيات الديكارتية إلى الإحداثيات القطبية والعكس بالعكس باستخدام الدوال المثلثية:[59]

x=r\cos \theta ,y=r\sin \theta

تتشكل أيضًا أنظمة الإحداثيات الأسطوانية والكروية، التي تعد إحداثيات قطبية معممة على ثلاثية الأبعاد، على أساس الدوال المثلثية. تُستخدم هذه الأنظمة في مشكلات مثل تكاملات ثلاثية الأبعاد لها تناظر أسطواني أو كروي.

المساحات

مثلث: هناك قانون يعبر عن مساحة المثلث بدلالة أضلاعه $a$ و $b$ والزاوية المحصورة بينهم θ دون الحاجة إلى معرفة ارتفاعه:[133]

S={1 \over 2}ab\sin \theta

متوازي أضلاع: يمكن ايجاد مساحته من خلال معرفة أطوال أضلاعه $a$ و $b$ وإحدى زواياه θ دون الحاجة إلى معرفة ارتفاعه بتطبيق هذا القانون:[134]

S=ab\sin \theta

مضلع منتظم: يمكن ايجاد مساحته من خلال تلك الصيغ:[63][135]

{\frac {1}{4}}nl^{2}\cdot \cot(\pi /n)\ =\ {\frac {1}{4n}}p^{2}\cdot \cot(\pi /n)

حيث

n

هو عدد أضلاعه، و

l

هو طول إحدى أضلاعه، و

p

هو محيط المضلع.

إذا كان المضلع محاط بدائرة نصف قطرها R ومحيط بدائرة نصف قطرها

r

(يُعتبَر أيضًا عامد المضلع[ملاحظة 27]):

{\frac {1}{2}}nR^{2}\cdot \sin(2\pi /n)\ =\ nr^{2}\tan(\pi /n)

المحيطات

مضلع منتظم: يمكن إيجاد محيطه بدلالة عدد أضلاعه $n$ والمسافة بين مركز المضلع وأحد رؤوسه $b$ ودالة الجيب:[136]

2nb\sin \left({\frac {\pi }{n}}\right)

قطع ناقص: يمكن إيجاد محيطه إنطلاقًا من نصف محوره الأكبر $a$ والأصغر $b$ باستخدام إحدى الدوال المثلثية:[137]

C\,=\,4a\int _{0}^{\pi /2}{\sqrt {1-e^{2}\sin ^{2}\theta }}\ d\theta \,=\,4a\,E(e)

حيث

e={\sqrt {1-b^{2}/a^{2}}}

هو معامل التباعد المركزي، و

E

هو التكامل الإهليلجي التام من النوع الثاني:

E(e)\,=\,\int _{0}^{\pi /2}{\sqrt {1-e^{2}\sin ^{2}\theta }}\ d\theta .

الحجوم

متوازي السطوح: يمكن تعبير عن حجمه بدلالة جيب التمام:

V=abc{\sqrt {1+2\cos(\alpha )\cos(\beta )\cos(\gamma )-\cos ^{2}(\alpha )-\cos ^{2}(\beta )-\cos ^{2}(\gamma )}}

حيث $\ \alpha =\angle ({\vec {b}},{\vec {c}}),\;\beta =\angle ({\vec {a}},{\vec {c}}),\;\gamma =\angle ({\vec {a}},{\vec {b}})$ ، و $a,b,c$ هن أطوال الأحرف.[138]

العلاقة بدالة الأس وبالأعداد المركبة

تمثيل عدد مركب على المستوي المركب

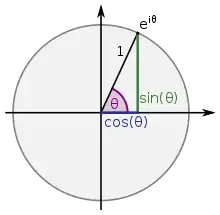
يمكن كتابة أي عدد مركب على الشكل المثلثي:

z=|z|(\cos \theta +i\sin \theta )

حيث

|z|

هو معيار العدد المركب، و

i

هي وحدة تخيلية مربعها يساوي مقابل واحد (

i^{2}=-1

).

يطلق على العلاقة بين الدالة الأسية والدوال المثلثية اسم صيغة أويلر:

e^{i\theta }=\cos \theta +i\sin \theta

إثبات: [139] نعتبر متسلسلة تايلور للدالة الأسية:

e^{x}=\sum _{n=0}^{\infty }{\frac {x^{n}}{n!}}=1+x+{\frac {x^{2}}{2!}}+{\frac {x^{3}}{3!}}+{\frac {x^{4}}{4!}}+{\frac {x^{5}}{5!}}+\cdots

بوضع: $x=i\theta$ ، تصبح المتسلسلة:

e^{i\theta }=1+i\theta -{\frac {\theta ^{2}}{2!}}-{\frac {i\theta ^{3}}{3!}}+{\frac {\theta ^{4}}{4!}}+{\frac {i\theta ^{5}}{5!}}-\cdots

e^{i\theta }=\left(1-{\frac {\theta ^{2}}{2!}}+{\frac {\theta ^{4}}{4!}}-\cdots \right)+i\left(\theta -{\frac {\theta ^{3}}{3!}}+{\frac {\theta ^{5}}{5!}}-\cdots \right)

من متسلسلات تايلور لكل من الجيب وجيب التمام، نستنتج أن:

e^{i\theta }=\cos \theta +i\sin \theta

لدينا:

${\begin{aligned}e^{i\theta }&=\cos \theta +i\sin \theta \\[5pt]e^{-i\theta }&=\cos \theta -i\sin \theta .\end{aligned}}$

قد تستعمل صيغة أويلر للحصول على بعض المتطابقات المثلثية، وذلك بكتابة دالتي الجيب والجيب التمام كما يلي:

\sin \theta ={\frac {e^{i\theta }-e^{-i\theta }}{2i}}\;

\cos \theta ={\frac {e^{i\theta }+e^{-i\theta }}{2}}\;

يمكن ملاحظة أن جيب التمام يمكن اعتباره الجزء الحقيقي والجيب هو الجزء التخيلي للدالة الأسية العقدية. رياضيا:

\cos \theta =\operatorname {Re} (e^{i\theta })

\sin \theta =\operatorname {Im} (e^{i\theta })

يعرف الشكل المعمم لصيغة أويلر بصيغة دي موافر:[140]

e^{in\theta }=(\cos \theta +i\sin \theta )^{n}=\cos(n\theta )+i\sin(n\theta )

أيضًا، باستخدام تعريف بواسطة متسلسلة ماكلورين للدوال الزائدية والمثلثية، يمكن الحصول على العلاقات بين تلك الدوال:

\sin z=\sum _{n=0}^{\infty }{\frac {(-1)^{n}}{(2n+1)!}}z^{2n+1}={\frac {e^{iz}-e^{-iz}}{2i}}={\frac {\sinh \left(iz\right)}{i}}

\cos z=\sum _{n=0}^{\infty }{\frac {(-1)^{n}}{(2n)!}}z^{2n}={\frac {e^{iz}+e^{-iz}}{2}}=\cosh \left(iz\right)

علم الفلك

استخدمت حساب المثلثات الكروية لعدة قرون لتحديد موقع الشمس والاقمار والنجوم، والتنبؤ بالكسوف والخسوف، ووصف مدارات الكواكب.

في العصر الحديث، تستخدم تقنية التثليث في علم الفلك لقياس مسافة النجوم القريبة، وكذلك في أنظمة الملاحة عبر الأقمار الصناعية.[141][142]

الخرائط

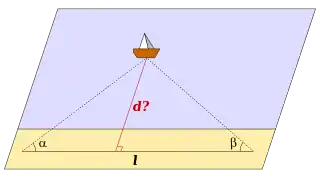
تستخدم عملية التثليث في إيجاد إحداثيات والبعد لسفينة بالنسبة للشاطئ وذلك بقياس الزوايا بين نقطتين مرجعيتين

حساب المثلثات هو أساس معظم ممارسات رسم الخرائط والمساحة. قياس زاوية باستخدام الجهاز أو بدون استخدامه، إسقاط الخرائط (تحويل سطح ناقصي إلى سطح مستوي)، وتحديد الارتفاعات، و حساب زاوية الإتجاه ^{[الإنجليزية]}، والمسح الاجتيازي المفتوح والمغلق،[ملاحظة 28] وتصميم الأقواس في انشاء الطرقات، جزء من تطبيقات الدوال المثلثية في مسح الأراضي.

على سبيل المثال، في التثليث، وهي إحدى الطرق القديمة للمساحة، نحسب احداثيات نقطة معينة من خلال قياس الزوايا بين نقطتين مرجعيتين، التي تُستخدم حاليًا في القياس البصري ثلاثي الأبعاد ^{[الإنجليزية]}. يُستخدَم في التثليث قانون جيب التمام وقانون الجيب لحساب زوايا المثلثات وتحديد الموقع الدقيق لكل نقطة.[143]

في هذه الحالة، تُحسَب المسافة بتطبيق هذا القانون:[144]

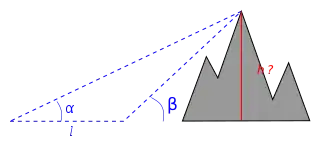
d={\frac {\sin \alpha \,\sin \beta }{\sin(\alpha +\beta )}}\ell ={\frac {\tan \alpha \,\tan \beta }{\tan \alpha +\tan \beta }}\ell

رسم توضيحي لكيفية حساب ارتفاع جبل.

مثال آخر في التثليث، إذا أراد المرء قياس ارتفاع h لجبل أو مبنى مرتفع، يتم تحديد الزوايا α، و β من نقطتين أرضيتين إلى الأعلى. لتكن ℓ مسافة بين هذه النقاط، يحسب الارتفاع بتطبيق هذا القانون:[145]

h={\frac {\sin \alpha \,\sin \beta }{\sin(\beta -\alpha )}}\ell ={\frac {\tan \alpha \,\tan \beta }{\tan \beta -\tan \alpha }}\ell .

متسلسلة فورييه وتحويل فورييه

دالتا الجيب وجيب التمام مثل كثيرات الحدود المتعامدة ولها استقلالية خطية. ومنهم يمكن كتابة أي دالة (دورية بشكل عام) على أنها العلاقة التالية بدلالة متسلسلة من تلك الدوال، والتي تسمى متسلسلة فورييه:[146]

f(x)={\frac {a_{0}}{2}}+\sum _{n=1}^{\infty }(a_{n}\cos nx+b_{n}\sin nx)

بالنسبة للدوال الفردية، فقط حدود دالة الجيب، أما الدوال الزوجية، فقط حدود دالة جيب التمام زائد معامل ثابت.

تحويل فورييه هو نوع من التحويل التكاملي وهو عبارة عن امتداد لمتسلسلة فورييه. يُعرف هذا التحويل بـ:[147]

F(\omega )={\frac {1}{\sqrt {2\pi }}}\int \limits _{-\infty }^{\infty }f(t)e^{-\mathrm {i} \omega t}\,dt

تُحوّل الدالة الأسية العقدية إلى دوال مثلثية بواسطة صيغة أويلر. تستخدم تحويل فورييه لحل المعادلات التفاضلية الجزئية مثل معادلة الموجة والتحليل الطيفي ومعالجة الإشارات.[148]

يستخدم تحويل فورييه أيضا في ضغط صور من النوع JPEG، حيث يستخدم فيها تحويل جيب التمام المتقطع، هذه الأخيرة، هي تقنية تمثل البيانات على شكل مجاميع دوال جيب التمام.[149]

الحركة التذبذبية (الاهتزازية)

صورة متحركة لموجة مربعية مع عدد متزايد من التوافقيات

الدوال المثلثية مهمة أيضا في الفيزياء. على سبيل المثال، يتم استخدام الجيب وجيب التمام لوصف الحركة التوافقية البسيطة، التي تنمذج العديد من الظواهر الطبيعية، مثل حركة كتلة متصلة بنابض،[150] وبالنسبة للزوايا الصغيرة، الحركة الرقاصية لكتلة معلقة بواسطة خيط،[151] وفي الهندسة الكهربائية، دراسة الدارات الكهربائية[84] مثل دارة الرنان التوافقي RLC. دوال الجيب وجيب التمام هي اسقاطات أحادية البعد لحركة دائرية منتظمة.

تثبت الدوال المثلثية أيضًا على أنها مفيدة في دراسة الدوال الدورية العامة. تُعد أنماط الموجات المميزة للدوال الدورية مفيدة لنمذجة الظواهر المتكررة مثل الصوت أو الموجات الضوئية.[152]

بشكل عام، يمكن التعبير عن دالة دورية $f (x)$ كمجموع موجات الجيب أو موجات جيب التمام في متسلسلات فورييه مثل موجة مربعية أو موجة سن المنشار.[153]

نرمز للدالة الحاوية للجيب أو جيب التمام بالرمز $φ k$ ، يأخذ مفكوك الدالة الدورية $f (t)$ الشكل:[154]

$f(t)=\sum _{k=1}^{\infty }c_{k}\varphi _{k}(t)$

حيث $c k$ هو معامل المتسلسلة.

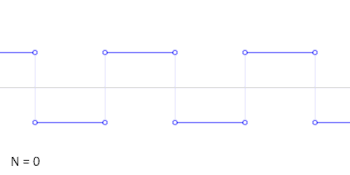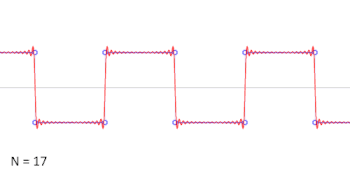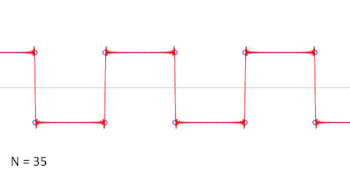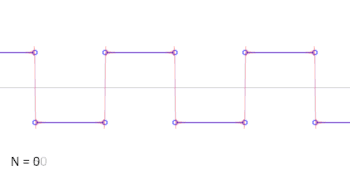
على سبيل المثال، يمكن كتابة الموجة المربعية كمتسلسلة فورييه:[155]

$f_{\text{square}}(t)={\frac {4}{\pi }}\sum _{k=1}^{\infty }{\sin {\big (}(2k-1)t{\big )} \over 2k-1}.$

في الرسوم المتحركة لموجة مربعية في أعلى اليسار، يمكن ملاحظة أن بعض الحدود فقط تنتج تقريبًا جيدًا إلى حد ما.

المعادلات الوسيطية

طالع أيضًا: معادلة وسيطية

منحنى ليساجو، كُوّن هذا الشكل باستعمال دوال تعتمد على الدوال المثلثية، حيث

\omega _{x}=5

و

\omega _{y}=4

يمكن تمثيل بعض المنحنيات الخاصة باستخدام المعادلات الوسيطية وبدلالة الدوال المثلثية، بعض الأمثلة على المنحنيات الخاصة هي كما يلي:

الدائرة: تعطى المعادلة الوسيطية للدائرة ذات المركز $(x_{0},y_{0})$ ونصف القطر $r$ بواسطة:[156]

{\begin{cases}x=r\,\cos(t)+x_{0}\\y=r\,\sin(t)+y_{0}\end{cases}}

القطع الناقص: يُمثَّل القطع الناقص ذو المركز $(x_{0},y_{0})$ ونصف المحور الكبير $a$ ونصف المحور الصغير $b$ كما يلي:[157]

{\begin{cases}x=a\,\cos(t)+x_{0}\\y=b\,\sin(t)+y_{0}\end{cases}}

منحنى ليساجو: تعطى الشكل الوسيطي لمنحنى ليساجو بواسطة:[158]

{\begin{cases}x=a\,\sin(\omega _{x}t+\delta )\\y=b\,\sin(\omega _{y}t+\gamma )\end{cases}}

حيث

\omega _{x}

و

\omega _{y}

هن عبارة عن ثوابت تصف عدد فصوص الشكل.

القطع الزائد، يمكن تمثيل وسيطيًا القطع الزائد الأفقي بواسطة:[157]

{\begin{cases}x=a\sec t+h\\y=b\tan t+k\end{cases}}

أو

{\begin{cases}x=\pm a\cosh t+h\\y=b\sinh t+k\end{cases}}

ويمكن تمثيل وسيطيًا القطع الزائد العمودي بواسطة:

{\begin{cases}x=a\tan t+h\\y=b\sec t+k\end{cases}}

أو

{\begin{cases}x=a\sinh t+h\\y=\pm b\cosh t+k\end{cases}}

حيث،

(h,k)

هي مركز القطع الزائد.

بالإضافة إلى تلك المنحنيات، يمكن أيضًا تمثيل عدة منحنيات التي تعتمد على الدوال المثلثية، بما في ذلك المنحنى العجلي التحتي، اللولب، السطوح الوسيطية ^{[الإنجليزية]}،... وهكذا.

البصريات

انكسار الضوء.

التطبيق الأساسي للدوال المثلثية في علم البصريات هو قانون سنيل. ينص هذا القانون، الذي ينطبق على ظاهرة انكسار الضوء، على العلاقة بين زوايا السقوط والانكسار:

{\frac {\sin \theta _{1}}{\sin \theta _{2}}}={\frac {v_{1}}{v_{2}}}={\frac {n_{2}}{n_{1}}}

حيث:

$θ 1$ : زاوية سقوط الموجة، $θ 2$ : زاوية انكسار الموجة.
$v 1$ : سرعة الضوء في الوسط الأول، $v 2$ : سرعة الضوء في الوسط الثاني.
$n 1$ : معامل الانكسار للوسط الأول، $n 2$ : معامل الانكسار للوسط الثاني

بالإضافة إلى انكسار الضوء، تُستخدم الدوال المثلثية في مجالات أخرى من البصريات، مثل تحليل تداخل الموجات والاستقطاب والحيود.[159]

الملاحة

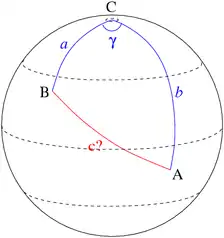
تاريخيا، استخدمت حساب المثلثات لتحديد احداثيات خطوط الطول والعرض لسفن الإبحار، ورسم المسارات، وحساب المسافات أثناء الملاحة.[67]

لا يزال حساب المثلثات مستخدمًا في الملاحة من خلال وسائل مثل نظام التموضع العالمي (GPS) والذكاء الاصطناعي للمركبات الذاتية.[71]

تُستخدم هذه المعادلة لتحديد المسافة بين نقطتين على الأرض:[ملاحظة 29]

\mathrm {AB} =R\arccos \left[\sin \lambda _{\mathrm {A} }\,\sin \lambda _{\mathrm {B} }+\cos \lambda _{\mathrm {A} }\,\cos \lambda _{\mathrm {B} }\,\cos \left(L_{\mathrm {A} }-L_{\mathrm {B} }\right)\right]

حيث:

$λ A$ و $λ B$ هما خطا عرض النقطتين المرغوبة.
$L A$ و $L B$ هما خطا طول النقطتين المرغوبة.
R هو نصف قطر الأرض.

يمكن إثبات ذلك من قانون جيب التمام للمثلثات الكروية.[67][160]

الفيزياء الميكانيكية

طالع أيضًا: حركة المقذوف
تصادم مرن

في الفيزياء الميكانيكية، تُطبق الدوال المثلثية على معادلات الحركة ثنائية الأبعاد وثلاثية الأبعاد، وحتى في دراسة حركة الأجسام. على سبيل المثال، عند تحليل الاختلافات الدورية في الحركيات والديناميكيات الدورانية، ومعادلات الزخم والزخم الزاوي، وظواهر التصادم، نستخدم فيها دوال مثلثية.[161]

قذف جسم من مبدأ المَعْلم

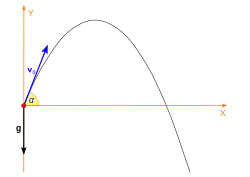
من أكثر التطبيقات المعروفة للدوال المثلثية في الميكانيكا هي دراسة ظاهرة حركة جسم مقذوف بزاوية $α$ ، وتكتب المعادلة الوسيطية لمسارها بدلالة الزمن $t$ على النحو التالي:

x(t)=v_{0}.t\cos \alpha

y(t)=-{\frac {1}{2}}gt^{2}+v_{0}.t\sin \alpha

حيث $x$ و $y$ هي إحداثيات موضع الجسم عند $t$ ثانية بعد السرعة الإبتدائية $v 0$ ، و $g$ هو تسارع الجاذبية.[162]

أيضا، يتم الحصول على سرعة الجسمين $v_{1}$ و $v_{2}$ ومقدار الزاويتين $\theta$ و $\varphi$ اللتين صنعهما الجسمان بعد التصادم المرن باستخدام الدوال المثلثية، بتطبيق قانون حفظ الزخم (في كلا المعادلتين، قبل تصادم جسمين (على اليسار) = بعد تصادم جسمين (على اليمين)):[163]

$\to m_{1}v_{1}+0=m_{1}v'_{1}\cos \theta +m_{2}v'_{2}\cos \varphi$ ثابت $P_{x}=$ : على المحور x

$\to 0+0=m_{1}v'_{1}\sin \theta -m_{2}v'_{2}\sin \varphi$ ثابت $P_{y}=$ : على المحور y

القبلة

حساب القبلة من مدينة يوغياكارتا الإندونيسية.

القبلة هي وجهة المصلي عند الصلاة وهي عند المسلمين الكعبة المشرفة في مدينة مكة.

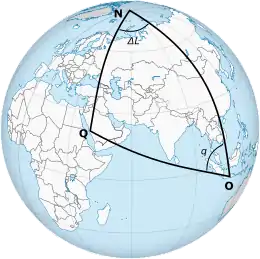
يتم تطبيق نموذج الدائرة العظمى لحساب القبلة باستخدام حساب المثلثات الكروية، وهو العلم الذي برع فيه العلماء المسلمين قديمًا واستقر العمل في تحديد القبلة عليه. في الشكل التالي، يشكل الموقع O والكعبة Q والقطب الشمالي N مثلثًا على الكرة الأرضية. يُشار إلى القبلة بـ OQ، وهو اتجاه الدائرة العظمى التي تشمل النقطتين O و Q. يمكن أيضًا التعبير عن القبلة كالزاوية $\angle NOQ$ (أو $\angle q$ ) للقبلة بالنسبة للشمال، وتسمى أيضًا "إنحراف القبلة". يمكن حساب هذه الزاوية كدالة رياضية لخط العرض المحلي $\Phi$ ، وخط عرض الكعبة $\Phi _{Q}$ ، وفرق بين خطي الطول لمنطقة ما والكعبة $\Delta L$ ،[164] هذه الدالة مستمدة من قاعدة ظل التمام التي تنطبق على أي مثلث كروي ذات الزوايا $A$ ، و $B$ ، و $C$ والجوانب $a$ ، و $b$ ، و $c$ :

$\cos a\,\cos C=\cot b\,\sin a-\cot B\,\sin C$ [165]

بتطبيق هذه الصيغة على المثلث الكروي $\triangle NOQ$ (بتعويض $B=\angle q=\angle NOQ$ )[166] وبتطبيق المتطابقات المثلثية، نحصل على:[ملاحظة 30]

$\cot q={\frac {\sin \Phi \cos \Delta L-\cos \Phi \tan \Phi _{Q}}{\sin \Delta L}}$ ، أو
$q=\cot ^{-1}{\frac {\sin \Phi \cos \Delta L-\cos \Phi \tan \Phi _{Q}}{\sin \Delta L}}$ [164]

الكهرباء والاتصالات

تمثيل دورة واحدة لنظام ثلاثي الطور من 0° إلى 360° (2π راديان) على طول المحور الزمني. يمثل المنحني اختلاف الجهد اللحظي (أو التيار) بدلالة الزمن. تتكرر هذه الدورة بتردد يعتمد على نظام القدرة الكهربائية.

تستخدم التيارات المتناوبة في تزويد المنازل والمصانع بالطاقة الكهربائية، ويُعبَّر عنها بشكل موجة جيبية. أحد الأسباب الرئيسية لتفضيل التيار المتردد على التيار المستمر في الصناعة هو إمكانية تحويل مستوى الجهد للتيار المتناوب باستخدام المحولات، وهذا يُقلل من الطاقة الضائعة عند النقل لمسافات طويلة ويجعلها ذات ربح عالٍ، بالإضافة لإمكانية عدم استعمال المبدلات في المولدات.[167][168]

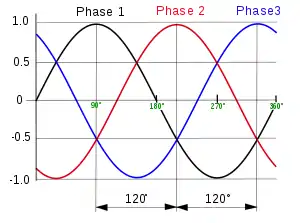
تولد محطات الكهرباء تيارات ثلاثية الطور في الغالب (انظر الصورة).[167] يمكن وصف تغير التيار المتناوب بتلك المعادلات: $v=V_{m}\sin(\omega t+\theta _{v})$ و $i=I_{m}\sin(\omega t+\theta _{i})$ [ملاحظة 31] وبالتالي تُحسب وتُحدد علاقات مختلفة مثل القدرة اللحظية ، القدرة الفعالة، القدرة غير الفعالة، ... إلخ، أو مفاهيم مثل تقدم الطور، وتأخر الطور وزاوية القدرة ومعامل القدرة، ...، من خلال تحليل الدوال المثلثية.[169] الكهرباء التي تُغذى بها المنازل هي موجة جيبية ترددها غالباً ما يكون 50 أو 60 هرتز.[167][168]

في نمذجة خط نقل الطاقة الكهربائية، تُنمذج محددات الخط بواسطة دوال زائدية.[168]

في أنظمة الاتصالات، عادة ما تدعم كل قناة الاتصال نقل إشاراتٍ فقط في نطاق ترددي معين، ويتعذر إرسال الإشارة عبر القناة إذا كان ترددها خارج هذا النطاق. ولذلك، من أجل إرسال إشارة لها تردد خارج النطاق، عادة ما يتم تثبيتها على موجة أخرى لها تردد متوافق مع نطاق القناة، تُسمَّى هذه التقنية التضمين. في الإشارات التشابهية تكون الموجة الحاملة موجة جيبية. على سبيل المثال، في تضمين المطال، يتم ضرب الإشارة التي تحتوي على المعلومات في الموجة الحاملة للموجة الجيبية.[170]

انظر أيضًا

في كومنز صور وملفات عن: دوال مثلثية

هوامش وملاحظات

وقد يُشار إليها أيضاً بـ ${\text{tg}}$ .
تُسمّى أيضاً دائرة مثلثية أو دائرة واحدية.
حيث k عدد صحيح كيفي.
أو تلك الرموز: cotan, cotg ctg, ctn
أو هذا الرمز: cosec
تم تدوين الشكل الانجليزي لأول مرة عام 1593 في الكتاب Horologiographia الخاص بـ Thomas Fale.
هناك مصادر مختلفة أنسبت الاستخدام الاول للمصطلح "sinus" إلى:
- إما ترجمة أفلاطون تيبورتينوس في عام 1116 لأعمال البتاني الخاصة بعلم الفلك.
- أو ترجمة جيراردو الكريموني لجبر الخوارزمي
- أو ترجمة روبرت أوف تشستر سنة 1145 لجداول الخوارزمي
- طالع:‏
  ‏Merlet, A Note on the History of the Trigonometric Functions in Ceccarelli (ed.), International Symposium on History of Machines and Mechanisms, Springer, 2004
- أو‏
  ‏Maor (1998), chapter 3, for an earlier etymology crediting Gerard.
- أو‏
  ‏Katx, Victor (July 2008). A history of mathematics (باللغة الإنجليزية) (الطبعة 3). Boston: Pearson. صفحة 210 (sidebar). ISBN 978-0321387004. الوسيط |CitationClass= تم تجاهله (مساعدة)
طالع فرع من قسم التاريخ "العصر الذهبي للحضارة الإسلامية" لمزيد من التفاصيل.
كانت العلاقة المثلثية لدالة الظل معروفة عند الهنود، ولكن لم يعتبروها كميةً مثلثيةً مستقلة كدالة الجيب.
الشريط الأفقي فوق الرقم يعني أن هذا الرقم يتكرر إلى ما لا نهاية.
المثلث القائم أو المثلث قائم الزاوية هو مثلثٌ إحدى زواياه قائمة، أي أن ضلعيه يشكلان زاوية قياسها $90^{\circ }$ .
يسمى أيضًا محور الفواصل أو محور الأفاصيل
عكس اتجاه عقارب الساعة لأجلِ زاويةٍ موجبةٍ $\theta >0$ ، وفي اتجاه عقارب الساعة من أجل زاويةٍ سالبةٍ $\theta <0$ .
يُسمّى أيضاً الفاصلة أو الأفصول.
يُسمّى أيضاً الترتيبة أو الأرتوب.
يسمى أيضًا محور العينات (في سوريا) أو محور التراتيب أو محور الأراتيب
نصف قطر التقارب لمتسلسلة قوى هو نصف قطر أكبر قرص تتقارب فيه المتسلسلة. وهو إما عدد حقيقي غير سالب أو ∞.
المعادلة الدالية هي أي معادلة التي متغيرها هي عبارة عن دالة.
تكون الدوال متعامدة إذا كان جدائهما الداخلي يساوي الصفر.
حيث: a هو ثابت حقيقي. s هو عدد مركب.
حيث:
- $\omega$ هي السرعة الزاوية.
- $\delta (\cdot )$ هي دالة ديراك.
$i$ $\text{[math]}$ هي وحدة تخيلية مربعها يساوي -1.
أطوال الأضلاع تساوي عدديًا قياس الزوايا التي تقابل أقواس الدائرة العظمى في المركز بالراديان. لذلك، بالنسبة لكرة ذات نصف قطر R لا يساوي الواحد، يجب قسمة أطوال الأضلاع على R قبل استخدام المتطابقة.
i هي وحدة تخيلية مربعها يساوي -1
تسمى أيضًا "أشعة" مفردها "شعاع".
وتسمى أيضا "جداء سلمي".
تسمى أيضا "ضرب اتجاهي" أو "جداء شعاعي"
عامد هو قطعة مستقيمة التي تربط مركز المضلع المنتظم بمنتصف أحد أضلاعه
المسح الاجتيازي هو طريقة لمسح منطقة مفتوحة أو مغلقة باستخدام قياس الزوايا والمسافات.
يجب تحويل الإحداثيات إلى الراديان في الحساب.
- إذا كان إحداثي خط العرض معبر عنه بالدرجات العشرية متبوع بـ N (التي تعني شمالاً)، يجب وضع إشارة "+" قبل قيمة خط العرض؛ وإذا كان متبوع بـ S (التي تعني جنوبًا)، نضع إشارة "-" قبل القيمة.
- بنفس الطريقة المذكورة أعلاه، إذا كان احداثي خط الطول بالدرجات العشرية متبوع بـ E (التي تعني شرقًا)، يجب وضع إشارة "+" قبل قيمة خط الطول؛ وإذا كان متبوع بـ W (التي تعني غربًا)، نضع إشارة "-" قبل القيمة.
- وإن كانت الإحداثيات معبر عنها بالدرجات والدقائق والثواني، يجب تحويلها إلى الدرجات العشرية، طالع قسم وحدات قياس الزوايا.
حيث:
- $i$ هي دالة التيار الكهربائي
- $v$ هي دالة الجهد الكهربائي
- $V_{m}$ و $I_{m}$ هما مطالا دالة التيار الكهربائي ودالة الجهد الكهربائي.
- $\omega$ هو التردد الزاوي.
- $\theta$ هو الطور الابتدائي.

مراجع

فهرس المراجع

د فرانك; موير, د روبرت (2004-03-01). سلسلة ملخصات شوم ايزي ; حساب المثلثات. international house for cultural investments. ISBN 978-977-282-145-7. مؤرشف من الأصل في 21 فبراير 2020. الوسيط |CitationClass= تم تجاهله (مساعدة)
محمد مفيد (2013-01-01). التكامل في الرياضات. مركز الكتاب الأكاديمي. ISBN 978-9957-35-052-9. مؤرشف من الأصل في 21 فبراير 2020. الوسيط |CitationClass= تم تجاهله (مساعدة)
ميشال إبراهيم ورامي أبو سليمان وفادي (2007-01-01). قاموس المصطلحات العلمية - انكليزي/فرنسي/عربي. دار الكتب العلمية. ISBN 978-2-7451-5445-3. مؤرشف من الأصل في 21 فبراير 2020. الوسيط |CitationClass= تم تجاهله (مساعدة)
Katx, Victor (July 2008). A history of mathematics (باللغة الإنجليزية) (الطبعة 3). Boston: Pearson. صفحة 210 (sidebar). ISBN 978-0321387004. الوسيط |CitationClass= تم تجاهله (مساعدة)
"Clark University". مؤرشف من الأصل في 18 ديسمبر 2017. الوسيط |CitationClass= تم تجاهله (مساعدة)
A Note on the History of the Trigonometric Functions in Ceccarelli (ed.), International Symposium on History of Machines and Mechanisms, Springer, 2004 See Maor (1998), chapter 3, for an earlier etymology crediting Gerard. See Katx, Victor (July 2008). A history of mathematics (باللغة الإنجليزية) (الطبعة 3). Boston: Pearson. صفحة 210 (sidebar). ISBN 978-0321387004. الوسيط |CitationClass= تم تجاهله (مساعدة) نسخة محفوظة 10 يونيو 2018 على موقع واي باك مشين.
كرلو (199?). علم الفلك. ktab INC. مؤرشف من الأصل في 12 أبريل 2020. الوسيط |CitationClass= تم تجاهله (مساعدة); تحقق من التاريخ في: |تاريخ= (مساعدة)
"5 معلومات مهمة عن المثلث وزوايا المثلث". إيد أرابيا. 2018-10-15. مؤرشف من الأصل في 22 ديسمبر 2019. اطلع عليه بتاريخ 12 أبريل 2020. الوسيط |CitationClass= تم تجاهله (مساعدة)
الرياضيات - المنهاج الجزائري القديم. 1999. الوسيط |CitationClass= تم تجاهله (مساعدة)
Max; Association, Research and Education (1984-01-01). Handbook of Mathematical, Scientific, and Engineering Formulas, Tables, Functions, Graphs, Transforms (باللغة الإنجليزية). Research & Education Assoc. ISBN 978-0-87891-521-7. مؤرشف من الأصل في 13 أبريل 2020. الوسيط |CitationClass= تم تجاهله (مساعدة)
Anthony (2007). Pure mathematics: Trigonometry (باللغة الإنجليزية). Pass Publications. ISBN 978-1-872684-87-1. مؤرشف من الأصل في 13 أبريل 2020. الوسيط |CitationClass= تم تجاهله (مساعدة)
Journal of Engineering for Industry (باللغة الإنجليزية). American Society of Mechanical Engineers. 1969. مؤرشف من الأصل في 13 أبريل 2020. الوسيط |CitationClass= تم تجاهله (مساعدة)
"Table of Domain and Range of Common Functions". www.analyzemath.com. مؤرشف من الأصل في 8 فبراير 2019. اطلع عليه بتاريخ 10 أبريل 2020. الوسيط |CitationClass= تم تجاهله (مساعدة)
Kim (2008-12-29). Mathematics in India (باللغة الإنجليزية). Princeton University Press. ISBN 978-1-4008-3407-5. مؤرشف من الأصل في 04 مارس 2020. الوسيط |CitationClass= تم تجاهله (مساعدة)
القانون المسعودي. 1. صفحة 275. الوسيط |CitationClass= تم تجاهله (مساعدة)
أبي الفتح إسماعيل بن مصطفى/شيخ زاده (2019-01-01). رسائل الكلنبوي في علم الفلك - رسالة الربع المجيب. دار الكتب العلمية. صفحة 151. ISBN 978-2-7451-8540-2. مؤرشف من الأصل في 1 يوليو 2020. الوسيط |CitationClass= تم تجاهله (مساعدة)
Oxford English Dictionary
Régis (1996). Encyclopedia of the History of Arabic Science (باللغة الإنجليزية). Psychology Press. ISBN 978-0-415-12411-9. مؤرشف من الأصل في 04 مارس 2020. الوسيط |CitationClass= تم تجاهله (مساعدة)
Gunter, Edmund (1620). Canon triangulorum. الوسيط |CitationClass= تم تجاهله (مساعدة)
B.B. Datta and A.N. Singh (1983). "Hindu Trigonometry" (PDF). Indian Journal of History of Science. 18 (1): 39–108. مؤرشف من الأصل (PDF) في 05 فبراير 2017. اطلع عليه بتاريخ 01 مارس 2010. الوسيط |CitationClass= تم تجاهله (مساعدة)
Team, Almaany. "تعريف و شرح و معنى تمام بالعربي في معاجم اللغة العربية معجم المعاني الجامع، المعجم الوسيط ،اللغة العربية المعاصرة ،الرائد ،لسان العرب ،القاموس المحيط - معجم عربي عربي صفحة 1". www.almaany.com (باللغة الإنجليزية). مؤرشف من الأصل في 22 أغسطس 2016. اطلع عليه بتاريخ 10 أبريل 2020. الوسيط |CitationClass= تم تجاهله (مساعدة)
Steven G. (2010-04). An Episodic History of Mathematics: Mathematical Culture Through Problem Solving (باللغة الإنجليزية). MAA. ISBN 978-0-88385-766-3. مؤرشف من الأصل في 20 يونيو 2020. الوسيط |CitationClass= تم تجاهله (مساعدة); تحقق من التاريخ في: |تاريخ= (مساعدة)
Howard (1983). Great Moments in Mathematics (before 1650) (باللغة الإنجليزية). MAA. ISBN 978-0-88385-310-8. مؤرشف من الأصل في 20 يونيو 2020. الوسيط |CitationClass= تم تجاهله (مساعدة)
Tobias (2012-10-02). Mathematics in Ancient Greece (باللغة الإنجليزية). Courier Corporation. ISBN 978-0-486-14998-1. مؤرشف من الأصل في 15 أبريل 2020. الوسيط |CitationClass= تم تجاهله (مساعدة)
Boyer, Carl B. (1991). A History of Mathematics (Second ed.). John Wiley & Sons, Inc. (ردمك 0-471-54397-7).
Toomer, G. (1998), Ptolemy's Almagest, Princeton University Press, ISBN 978-0-691-00260-6 الوسيط |CitationClass= تم تجاهله (مساعدة); الوسيط |separator= تم تجاهله (مساعدة)CS1 maint: ref=harv (link)
موسوعة تاريخ العلوم العربية - ثلاثة مجلدات. مؤرشف من الأصل في 12 أكتوبر 2016. الوسيط |CitationClass= تم تجاهله (مساعدة)
O'Connor; Robertson. "Madhava of Sangamagrama". School of Mathematics and Statistics University of St Andrews, Scotland. مؤرشف من الأصل في 14 مايو 2006. اطلع عليه بتاريخ 08 سبتمبر 2007. الوسيط |CitationClass= تم تجاهله (مساعدة)
Gingerich, Owen (1986). "Islamic Astronomy". ساينتفك أمريكان. المجلد. 254. صفحة 74. مؤرشف من الأصل في 19 أكتوبر 2013. اطلع عليه بتاريخ 13 يوليو 2010. الوسيط |CitationClass= تم تجاهله (مساعدة)
"History of Trigonometry - Part 3". nrich.maths.org. مؤرشف من الأصل في 20 فبراير 2020. اطلع عليه بتاريخ 05 أبريل 2020. الوسيط |CitationClass= تم تجاهله (مساعدة)
Jacques Sesiano, "Islamic mathematics", p. 157, in Selin, Helaine; D'Ambrosio, Ubiratan, المحررون (2000). Mathematics Across Cultures: The History of Non-western Mathematics. Springer. ISBN 1-4020-0260-2. الوسيط |CitationClass= تم تجاهله (مساعدة)
"trigonometry". Encyclopedia Britannica. مؤرشف من الأصل في 12 مايو 2015. الوسيط |CitationClass= تم تجاهله (مساعدة)
أبو الريحان البيروني (2002-01-01). القانون المسعودي 1-3 ج1. دار الكتب العلمية. صفحة 225. ISBN 978-2-7451-3305-2. مؤرشف من الأصل في 22 يونيو 2020. الوسيط |CitationClass= تم تجاهله (مساعدة)
Adolph P. Yushkevich. История математики. С древнейших времен до начала Нового времени (باللغة الروسية). الوسيط |CitationClass= تم تجاهله (مساعدة)
مجلة تاريخ العلوم العربية (باللغة الإنجليزية). Institute for the History of Arabic Science, University of Aleppo. 1977. مؤرشف من الأصل في 20 يونيو 2020. الوسيط |CitationClass= تم تجاهله (مساعدة)
إبراهيم (2002-01-01). دليل الأوائل. ktab INC. مؤرشف من الأصل في 20 يونيو 2020. الوسيط |CitationClass= تم تجاهله (مساعدة)
المعلم الجديد. المجلد 30. الوسيط |CitationClass= تم تجاهله (مساعدة)
Florian (1898). A History of Elementary Mathematics (باللغة الإنجليزية). Macmillan. الوسيط |CitationClass= تم تجاهله (مساعدة)
Ravi P.; Sen, Syamal K. (2014-11-11). Creators of Mathematical and Computational Sciences (باللغة الإنجليزية). Springer. ISBN 978-3-319-10870-4. مؤرشف من الأصل في 18 مايو 2020. الوسيط |CitationClass= تم تجاهله (مساعدة)
مصطفى (2005-01-01). موسوعة علماء العرب والمسلمين وأعلامهم. Al Manhal. ISBN 9796500011424. مؤرشف من الأصل في 12 أبريل 2020. الوسيط |CitationClass= تم تجاهله (مساعدة)
Dirk Jan (1967). A Concise History of Mathematics (باللغة الإنجليزية). Courier Corporation. ISBN 978-0-486-60255-4. مؤرشف من الأصل في 03 مارس 2020. الوسيط |CitationClass= تم تجاهله (مساعدة)
Donald Routledge Hill (1996), "Engineering", in Roshdi Rashed, Encyclopedia of the History of Arabic Science, Vol. 3, p. 751–795 [769].
O'Connor, John J.; Robertson, Edmund F., "Abu Arrayhan Muhammad ibn Ahmad al-Biruni", تاريخ ماكتوتور لأرشيف الرياضيات الوسيط |CitationClass= تم تجاهله (مساعدة); الوسيط |separator= تم تجاهله (مساعدة)CS1 maint: ref=harv (link)
Elias C.; Tonias, Constantine N. (2016-04-28). Geometric Procedures for Civil Engineers (باللغة الإنجليزية). Springer. ISBN 978-3-319-24295-8. مؤرشف من الأصل في 21 يونيو 2020. الوسيط |CitationClass= تم تجاهله (مساعدة)
نوال حسن; الخليج, دار (2017-01-01). العلوم عند العرب والمسلمين. دار الخليج للنشر والتوزيع / daralkhalij for Publishing and Distribution. ISBN 978-9957-519-85-8. مؤرشف من الأصل في 12 أبريل 2020. الوسيط |CitationClass= تم تجاهله (مساعدة)
Clifford A. (2009). The Math Book: From Pythagoras to the 57th Dimension, 250 Milestones in the History of Mathematics (باللغة الإنجليزية). Sterling Publishing Company, Inc. ISBN 978-1-4027-5796-9. مؤرشف من الأصل في 15 مايو 2020. الوسيط |CitationClass= تم تجاهله (مساعدة)
قرقور, يوسف. "ملك سرقسطة المؤتمن بن هود ومبرهنة فيثاغورس: مصادرها وامتداداتها" (PDF). ISSN 0210-8615. مؤرشف من الأصل (PDF) في 29 يونيو 2017. الوسيط |CitationClass= تم تجاهله (مساعدة); Cite journal requires |journal= (مساعدة)
Marlow Anderson, Victor J. Katz, Robin J. Wilson (2004), Sherlock Holmes in Babylon and Other Tales of Mathematical History, جمعية الرياضيات الأمريكية, صفحة 139, ISBN 0883855461 الوسيط |CitationClass= تم تجاهله (مساعدة); الوسيط |separator= تم تجاهله (مساعدة)CS1 maint: ref=harv (link)
George Gheverghese (2011). The Crest of the Peacock: Non-European Roots of Mathematics (Third Edition) (باللغة الإنجليزية). Princeton University Press. ISBN 978-0-691-13526-7. الوسيط |CitationClass= تم تجاهله (مساعدة)
Katz 2007، p. 308
O'Connor, John J.; Robertson, Edmund F., "دوال مثلثية", تاريخ ماكتوتور لأرشيف الرياضيات الوسيط |CitationClass= تم تجاهله (مساعدة); الوسيط |separator= تم تجاهله (مساعدة)CS1 maint: ref=harv (link)
Carl B. (2012-10-09). The History of the Calculus and Its Conceptual Development (باللغة الإنجليزية). Courier Corporation. ISBN 978-0-486-17538-6. مؤرشف من الأصل في 12 أبريل 2020. الوسيط |CitationClass= تم تجاهله (مساعدة)
"Fincke biography". مؤرشف من الأصل في 07 يناير 2017. اطلع عليه بتاريخ 15 مارس 2017. الوسيط |CitationClass= تم تجاهله (مساعدة)
Bourbaki, Nicolás (1994). Elements of the History of Mathematics. Springer. مؤرشف من الأصل في 16 فبراير 2020. الوسيط |CitationClass= تم تجاهله (مساعدة)
Robert E. Bradley, Lawrence A. D'Antonio, Charles Edward Sandifer. Euler at 300: an appreciation. Mathematical Association of America, 2007. Page 100.
أبو الريحان البيروني. القانون المسعودي. 1. صفحة 321. الوسيط |CitationClass= تم تجاهله (مساعدة)
Nielsen (1966, pp. xxiii–xxiv)
Glen Van (2020-01-23). Trigonometry: a Very Short Introduction (باللغة الإنجليزية). Oxford University Press. ISBN 978-0-19-881431-3. مؤرشف من الأصل في 12 أبريل 2020. الوسيط |CitationClass= تم تجاهله (مساعدة)
George Brinton; Weir, Maurice D.; Hass, Joel (2010). Thomas' Calculus (باللغة الإنجليزية). Pearson. ISBN 978-0-321-64363-6. مؤرشف من الأصل في 19 فبراير 2020. الوسيط |CitationClass= تم تجاهله (مساعدة)
Richard A. (2014-04-15). Modern Calculus and Analytic Geometry (باللغة الإنجليزية). Courier Corporation. ISBN 978-0-486-79398-6. مؤرشف من الأصل في 25 فبراير 2020. الوسيط |CitationClass= تم تجاهله (مساعدة)
Lindeburg, Michael R. (2012). Civil Engineering Reference Manual for the PE Exam. Professional Publications, Inc. صفحة 78-7. ISBN 978-1-59126-380-7. الوسيط |CitationClass= تم تجاهله (مساعدة)
Benjamin (1861). Elements of Plane and Spherical Trigonometry: With Practical Applications (باللغة الإنجليزية). R. S. Davis. الوسيط |CitationClass= تم تجاهله (مساعدة)
Tim (2019-05-23). The Essential Calculus Workbook: Trigonometric Functions (باللغة الإنجليزية). Questing Vole Press. مؤرشف من الأصل في 28 فبراير 2020. الوسيط |CitationClass= تم تجاهله (مساعدة)
Geoffrey C.; Rockett, Andrew M. (2015-01-01). Applied Calculus (باللغة الإنجليزية). Cengage Learning. ISBN 978-1-305-46505-3. مؤرشف من الأصل في 24 فبراير 2020. الوسيط |CitationClass= تم تجاهله (مساعدة)
Protter & Morrey (1970, pp. APP-2,APP-3)
Heng, Cheng and Talbert, "Additional Mathematics" نسخة محفوظة 2015-03-20 على موقع واي باك مشين., page 228
Coxford, Arthur (1987). Trigonometry. الوسيط |CitationClass= تم تجاهله (مساعدة)
Bityutskov, V.I. (2011-02-07). "Trigonometric Functions". Encyclopedia of Mathematics (باللغة الإنجليزية). مؤرشف من الأصل في 29 ديسمبر 2017. اطلع عليه بتاريخ 29 ديسمبر 2017. الوسيط |CitationClass= تم تجاهله (مساعدة)
Weisstein, Eric W. "Circular Functions". mathworld.wolfram.com (باللغة الإنجليزية). مؤرشف من الأصل في 3 أبريل 2017. اطلع عليه بتاريخ 01 مارس 2020. الوسيط |CitationClass= تم تجاهله (مساعدة)
د فرانك; موير, د روبرت (2004-03-01). سلسلة ملخصات شوم ايزي ; حساب المثلثات. international house for cultural investments. ISBN 978-977-282-145-7. مؤرشف من الأصل في 25 فبراير 2020. الوسيط |CitationClass= تم تجاهله (مساعدة)
Larson, Ron (2013). Trigonometry (الطبعة 9th). Cengage Learning. صفحة 153. ISBN 978-1-285-60718-4. مؤرشف من الأصل في 15 فبراير 2018. الوسيط |CitationClass= تم تجاهله (مساعدة) Extract of page 153 نسخة محفوظة 2018-02-15 على موقع واي باك مشين.
Schaumberger, Norman (1974-01-01). "A Classroom Theorem on Trigonometric Irrationalities". The Two-Year College Mathematics Journal. 5 (1): 73–76. doi:10.2307/3026991. مؤرشف من الأصل في 13 أكتوبر 2019. الوسيط |CitationClass= تم تجاهله (مساعدة)
Niven, Ivan (1956). Irrational Numbers. Mathematical Association of America. صفحة 41. MR = 0080123 0080123. مؤرشف من الأصل في 9 يونيو 2020. الوسيط |CitationClass= تم تجاهله (مساعدة)
A proof for the cosine case appears as Lemma 12 in Bennett, Curtis D.; Glass, A. M. W.; Székely, Gábor J. (2004). "Fermat's last theorem for rational exponents". American Mathematical Monthly. 111 (4): 322–329. doi:10.2307/4145241. JSTOR 4145241. MR = 2057186 2057186. الوسيط |CitationClass= تم تجاهله (مساعدة)
يتم الحصول على قيم دقيقة للدوال باستخدام متطابقات مجموع أو فرق زاويتين، على سبيل المثال: $cos(15°)=cos(60° - 45°)$
Weisstein, Eric W. "Trigonometry Angles--Pi/9". mathworld.wolfram.com (باللغة الإنجليزية). مؤرشف من الأصل في 30 ديسمبر 2019. اطلع عليه بتاريخ 04 أبريل 2020. الوسيط |CitationClass= تم تجاهله (مساعدة)
M. Ram; Rath, Purusottam (2014-06-24). Transcendental Numbers (باللغة الإنجليزية). Springer. ISBN 978-1-4939-0832-5. مؤرشف من الأصل في 12 أبريل 2020. الوسيط |CitationClass= تم تجاهله (مساعدة)
Abramowitz, Milton and Irene A. Stegun, p.74
Milton; Stegun, Irene A. (1965-01-01). Handbook of Mathematical Functions: With Formulas, Graphs, and Mathematical Tables (باللغة الإنجليزية). Courier Corporation. ISBN 978-0-486-61272-0. مؤرشف من الأصل في 25 فبراير 2020. الوسيط |CitationClass= تم تجاهله (مساعدة)
"«FORMULAS FOR nth ORDER DERIVATIVES OF HYPERBOLIC. AND TRIGONOMETRIC FUNCTIONS»" (PDF). NASA. مؤرشف من الأصل (PDF) في 12 مارس 2017. الوسيط |CitationClass= تم تجاهله (مساعدة)
Timothy; Barrow-Green, June; Leader, Imre (2010-07-18). The Princeton Companion to Mathematics (باللغة الإنجليزية). Princeton University Press. ISBN 978-1-4008-3039-8. مؤرشف من الأصل في 19 فبراير 2020. الوسيط |CitationClass= تم تجاهله (مساعدة)
Trigonometric functions. V.I. Bityutskov (originator), Encyclopedia of Mathematics. نسخة محفوظة 19 فبراير 2020 على موقع واي باك مشين.
"Sine: Introduction to the trigonometric functions (subsection Trigonometrics/05)". functions.wolfram.com. مؤرشف من الأصل في 2 مايو 2016. اطلع عليه بتاريخ 14 أبريل 2020. الوسيط |CitationClass= تم تجاهله (مساعدة)
William E. Boyce, Richard C. DiPrima, Douglas B. Meade. Elementary Differential Equations and Boundary Value Problems (باللغة الإنجليزية). الوسيط |CitationClass= تم تجاهله (مساعدة)صيانة CS1: أسماء متعددة: قائمة المؤلفون (link)
Thomas & Finney 1996، §8.9
Thomas & Finney 1996, §8.9. الوسيط |CitationClass= تم تجاهله (مساعدة)
Ahlfors, pages 43–44.
Michael T. (2007-06-18). Introduction to Mathematical Physics (باللغة الإنجليزية). John Wiley & Sons. ISBN 978-3-527-40627-2. مؤرشف من الأصل في 12 أبريل 2020. الوسيط |CitationClass= تم تجاهله (مساعدة)
Abramowitz; Weisstein.
Weisstein, Eric W. "Pole". mathworld.wolfram.com (باللغة الإنجليزية). مؤرشف من الأصل في 18 مارس 2020. اطلع عليه بتاريخ 09 أبريل 2020. الوسيط |CitationClass= تم تجاهله (مساعدة)
Stanley, Enumerative Combinatorics, Vol I., page 149
Green, Robin. "Faster Math Functions" (PDF). صفحة 6–7. مؤرشف من الأصل (PDF) في 23 مارس 2020. الوسيط |CitationClass= تم تجاهله (مساعدة)
Aigner, Martin; Ziegler, Günter M. (2000). Proofs from THE BOOK (الطبعة Second). سبرنجر. صفحة 149. ISBN 978-3-642-00855-9. مؤرشف من الأصل في 08 مارس 2014. الوسيط |CitationClass= تم تجاهله (مساعدة)
Remmert, Reinhold (1991). Theory of complex functions. Springer. صفحة 327. ISBN 978-0-387-97195-7. مؤرشف من الأصل في 20 مارس 2015. الوسيط |CitationClass= تم تجاهله (مساعدة) Extract of page 327 نسخة محفوظة 2015-03-20 على موقع واي باك مشين.
Omar (2016-02-09). Introduction to Calculus and Classical Analysis (باللغة الإنجليزية). Springer. ISBN 978-3-319-28400-2. مؤرشف من الأصل في 12 أبريل 2020. الوسيط |CitationClass= تم تجاهله (مساعدة)
Luis Manuel Braga da Costa (2012-04-04). Transcendental Representations with Applications to Solids and Fluids (باللغة الإنجليزية). CRC Press. ISBN 978-1-4398-3431-2. مؤرشف من الأصل في 03 مارس 2020. الوسيط |CitationClass= تم تجاهله (مساعدة)
Kannappan, Palaniappan (2009). Functional Equations and Inequalities with Applications. Springer. ISBN 978-0387894911. الوسيط |CitationClass= تم تجاهله (مساعدة)
John H.; Howell, Russell W. (2006). Complex Analysis for Mathematics and Engineering (باللغة الإنجليزية). Jones & Bartlett Learning. ISBN 978-0-7637-3748-1. مؤرشف من الأصل في 22 مارس 2016. الوسيط |CitationClass= تم تجاهله (مساعدة)
Gandhi, Viswanathan (07-10-2014). "Domain coloring for visualizing complex functions". مؤرشف من الأصل في 12 أبريل 2020. الوسيط |CitationClass= تم تجاهله (مساعدة); تحقق من التاريخ في: |تاريخ= (مساعدة)
The Princeton Companion to Mathematics. صفحة 307 - 308. الوسيط |CitationClass= تم تجاهله (مساعدة)
Olver, NIST Handbook of Mathematical Functions. صفحة 122. الوسيط |CitationClass= تم تجاهله (مساعدة)
Elementary Differential Equations and Boundary Value Problems. صفحة 376. الوسيط |CitationClass= تم تجاهله (مساعدة)
David W. (2008-01-17). A First Course in Fourier Analysis (باللغة الإنجليزية). Cambridge University Press. ISBN 978-1-139-46903-6. مؤرشف من الأصل في 12 مارس 2020. الوسيط |CitationClass= تم تجاهله (مساعدة)
Marcus (2010-01-07). Linear Partial Differential Equations and Fourier Theory (باللغة الإنجليزية). Cambridge University Press. ISBN 978-0-521-19970-4. مؤرشف من الأصل في 13 أبريل 2020. الوسيط |CitationClass= تم تجاهله (مساعدة)
"More Approximations to Trigonometric Functions" (PDF). مؤرشف من الأصل (PDF) في 23 مارس 2020. الوسيط |CitationClass= تم تجاهله (مساعدة)
Kantabutra, Vitit (1996). "On hardware for computing exponential and trigonometric functions" – عبر IEEE Transactions on Computers. الوسيط |CitationClass= تم تجاهله (مساعدة)
Jurgen; Platzner, Marco (2004-08-19). Field Programmable Logic and Application: 14th International Conference , FPL 2004, Leuven, Belgium, August 30-September 1, 2004, Proceedings (باللغة الإنجليزية). Springer Science & Business Media. ISBN 978-3-540-22989-6. مؤرشف من الأصل في 12 أبريل 2020. الوسيط |CitationClass= تم تجاهله (مساعدة)
"التنفیذ المادي باستخدام FPGA لخوارزمیتي كوردك وجدول المقارنة لحساب الدوال الریاضیة الأولیة". المجلات الأكاديمية العلمية العراقية. مؤرشف من الأصل في 12 أبريل 2020. الوسيط |CitationClass= تم تجاهله (مساعدة)
P, BrentRichard (1976-04-01). "Fast Multiple-Precision Evaluation of Elementary Functions". Journal of the ACM (JACM) (باللغة الإنجليزية). doi:10.1145/321941.321944. مؤرشف من الأصل في 12 أبريل 2020. الوسيط |CitationClass= تم تجاهله (مساعدة)
"Weierstrass Substitution". Math24 (باللغة الإنجليزية). مؤرشف من الأصل في 27 مارس 2020. اطلع عليه بتاريخ 27 مارس 2020. الوسيط |CitationClass= تم تجاهله (مساعدة)
Selby 1970، pg. 190
Abramowitz and Stegun. Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables. صفحة 72. الوسيط |CitationClass= تم تجاهله (مساعدة)
غياث الدين الكاشي. مفتاح الحساب. الوسيط |CitationClass= تم تجاهله (مساعدة)
Clifford A. (2009). The Math Book: From Pythagoras to the 57th Dimension, 250 Milestones in the History of Mathematics (باللغة الإنجليزية). Sterling Publishing Company, Inc. ISBN 978-1-4027-5796-9. مؤرشف من الأصل في 30 مارس 2017. الوسيط |CitationClass= تم تجاهله (مساعدة)
Romuald Ireneus 'Scibor-Marchocki, Spherical trigonometry, Elementary-Geometry Trigonometry web page (1997). نسخة محفوظة 21 أبريل 2020 على موقع واي باك مشين.
W. Gellert, S. Gottwald, M. Hellwich, H. Kästner, and H. Küstner, The VNR Concise Encyclopedia of Mathematics, 2nd ed., ch. 12 (Van Nostrand Reinhold: New York, 1989).
Todhunter, I. (1886). Spherical Trigonometry (الطبعة 5th). MacMillan. مؤرشف من الأصل في 14 أبريل 2020. الوسيط |CitationClass= تم تجاهله (مساعدة)
The Universal Encyclopaedia of Mathematics, Pan Reference Books, 1976, page 529-530. English version George Allen and Unwin, 1964. Translated from the German version Meyers Rechenduden, 1960.
Daniel Zwillinger, CRC Standard Mathematical Tables and Formulae, 32nd Edition, CRC Press, 2011, page 219.
Modern calculus with analytic geometry, Volume 1. صفحة 105-106. الوسيط |CitationClass= تم تجاهله (مساعدة)
Calculus and Analytic Geometry. صفحة 138. الوسيط |CitationClass= تم تجاهله (مساعدة)
Olver, NIST Handbook of Mathematical Functions. صفحة 116. الوسيط |CitationClass= تم تجاهله (مساعدة)
Ernest William (1891). A Treatise on Plane Trigonometry (باللغة الإنجليزية). University Press. مؤرشف من الأصل في 12 أبريل 2020. الوسيط |CitationClass= تم تجاهله (مساعدة)
Michael Sullivan, Trigonometry, Dellen Publishing Company, 1988, page 243.
W. A. Beyer, J. D. Louck, and D. Zeilberger, A Generalization of a Curiosity that Feynman Remembered All His Life, Math. Mag. 69, 43–44, 1996.
Arthur Graham; Frink, Fred Goodrich ([c1909]). Plane trigonometry. New York : Henry Holt. مؤرشف من الأصل في 13 أبريل 2020. الوسيط |CitationClass= تم تجاهله (مساعدة); تحقق من التاريخ في: |تاريخ= (مساعدة)
Weisstein, Eric W. "Inverse Trigonometric Functions". mathworld.wolfram.com (باللغة الإنجليزية). مؤرشف من الأصل في 13 أبريل 2020. اطلع عليه بتاريخ 13 أبريل 2020. الوسيط |CitationClass= تم تجاهله (مساعدة)
V. G.; Argunov, B. I.; Skornyakov, L. A.; Boltyanskii, V. G. (2013-11-07). Hyperbolic Functions: with Configuration Theorems and Equivalent and Equidecomposable Figures (باللغة الإنجليزية). Courier Corporation. ISBN 978-0-486-17005-3. مؤرشف من الأصل في 12 أبريل 2020. الوسيط |CitationClass= تم تجاهله (مساعدة)
"Hyperbolic functions" (PDF). Mathcentre. 9 يناير 2006. مؤرشف من الأصل (PDF) في 9 سبتمبر 2019. الوسيط |CitationClass= تم تجاهله (مساعدة)
Árpád (2010-05-25). Generalized Bessel Functions of the First Kind (باللغة الإنجليزية). Springer Science & Business Media. ISBN 978-3-642-12229-3. مؤرشف من الأصل في 14 مارس 2020. الوسيط |CitationClass= تم تجاهله (مساعدة)
United States National Bureau of (1952). Tables of Chebyshev Polynomials (باللغة الإنجليزية). U.S. Government Printing Office. مؤرشف من الأصل في 14 مارس 2020. الوسيط |CitationClass= تم تجاهله (مساعدة)
Robert; Halliday, David; Krane, Kenneth S. (1992-03-16). Physics (باللغة الإنجليزية). Wiley. ISBN 978-0-471-80457-4. مؤرشف من الأصل في 19 فبراير 2020. الوسيط |CitationClass= تم تجاهله (مساعدة)
"Area Formulas". www.math.com. مؤرشف من الأصل في 15 مايو 2020. اطلع عليه بتاريخ 21 مايو 2020. الوسيط |CitationClass= تم تجاهله (مساعدة)
"Area of Triangle Using Trigonometry - MathBitsNotebook(Geo - CCSS Math)". mathbitsnotebook.com. مؤرشف من الأصل في 29 أكتوبر 2019. اطلع عليه بتاريخ 21 مايو 2020. الوسيط |CitationClass= تم تجاهله (مساعدة)
Aaron (1875). Plane and Spherical Trigonometry and Mensuration (باللغة الإنجليزية). American Book Company. مؤرشف من الأصل في 22 مايو 2020. الوسيط |CitationClass= تم تجاهله (مساعدة)
Max; Association, Research and Education (1984-01-01). Handbook of Mathematical, Scientific, and Engineering Formulas, Tables, Functions, Graphs, Transforms (باللغة الإنجليزية). Research & Education Assoc. ISBN 978-0-87891-521-7. مؤرشف من الأصل في 22 مايو 2020. الوسيط |CitationClass= تم تجاهله (مساعدة)
Ron; Edwards, Bruce H. (2010-01-01). Calculus of a Single Variable: Early Transcendental Functions (باللغة الإنجليزية). Cengage Learning. ISBN 978-0-538-73552-0. مؤرشف من الأصل في 22 مايو 2020. الوسيط |CitationClass= تم تجاهله (مساعدة)
Isaac (1878). Spherical Trigonometry, for the Use of Colleges and Schools: With Numerous Examples (باللغة الإنجليزية). Macmillan. الوسيط |CitationClass= تم تجاهله (مساعدة)
Gilbert (1991-01-01). Calculus (باللغة الإنجليزية). SIAM. ISBN 978-0-9614088-2-4. مؤرشف من الأصل في 12 أبريل 2020. الوسيط |CitationClass= تم تجاهله (مساعدة)
Milton; Stegun, Irene A. (2012-04-30). Handbook of Mathematical Functions: with Formulas, Graphs, and Mathematical Tables (باللغة الإنجليزية). Courier Corporation. ISBN 978-0-486-15824-2. مؤرشف من الأصل في 19 فبراير 2020. الوسيط |CitationClass= تم تجاهله (مساعدة)
An Elementary Treatise on Plane and Spherical Trigonometry with their applications to navigation, surveying heights and distances, and spherical astronomy; and particularly adapted to explaining the construction of Bowditch's Navigator ... Third edition, with additions (باللغة الإنجليزية). 1845. مؤرشف من الأصل في 12 أبريل 2020. الوسيط |CitationClass= تم تجاهله (مساعدة)
Michael; Backman, Dana (2009-01-05). Astronomy: The Solar System and Beyond (باللغة الإنجليزية). Cengage Learning. ISBN 978-0-495-56203-0. مؤرشف من الأصل في 12 أبريل 2020. الوسيط |CitationClass= تم تجاهله (مساعدة)
عاصی، محمدرضا. نقشه‌برداری (ژئوماتیک) (ویراست چهارم) (باللغة الفارسية). انتشارات علمی دانشگاه ضنعتی شریف. ISBN 978-964-208-008-3. الوسيط |CitationClass= تم تجاهله (مساعدة)
"Solving ASA Triangles". www.mathsisfun.com. مؤرشف من الأصل في 01 يوليو 2018. اطلع عليه بتاريخ 28 مايو 2020. الوسيط |CitationClass= تم تجاهله (مساعدة)
Геометрия. 7-9 классы. Учебник. ФГОС, размер 165x220 мм. Атанасян Левон Сергеевич (باللغة الروسية). ISBN 978-5-09-021136-9. الوسيط |CitationClass= تم تجاهله (مساعدة)
N. K. (2014-05-12). A Treatise on Trigonometric Series: Volume 1 (باللغة الإنجليزية). Elsevier. ISBN 978-1-4832-2419-0. مؤرشف من الأصل في 12 أبريل 2020. الوسيط |CitationClass= تم تجاهله (مساعدة)
Weisstein, Eric W. "Fourier Transform". mathworld.wolfram.com (باللغة الإنجليزية). مؤرشف من الأصل في 18 مارس 2020. اطلع عليه بتاريخ 14 أبريل 2020. الوسيط |CitationClass= تم تجاهله (مساعدة)
Gerald B Folland. Fourier Analysis and its Applications. صفحات 225–234. الوسيط |CitationClass= تم تجاهله (مساعدة)
"JPEG (Transform Compression)". www.dspguide.com. مؤرشف من الأصل في 20 يناير 2020. اطلع عليه بتاريخ 11 أبريل 2020. الوسيط |CitationClass= تم تجاهله (مساعدة)
James R. (2010-11-08). Differential Equations with Boundary Value Problems: An Introduction to Modern Methods & Applications (باللغة الإنجليزية). John Wiley & Sons. ISBN 978-0-470-59535-0. مؤرشف من الأصل في 03 مارس 2020. الوسيط |CitationClass= تم تجاهله (مساعدة)
Morris; Pollard, Harry (1985-10-01). Ordinary Differential Equations: An Elementary Textbook for Students of Mathematics, Engineering, and the Sciences (باللغة الإنجليزية). Courier Corporation. ISBN 978-0-486-64940-5. مؤرشف من الأصل في 03 مارس 2020. الوسيط |CitationClass= تم تجاهله (مساعدة)
Farlow, Stanley J. (1993). Partial differential equations for scientists and engineers (الطبعة Reprint of Wiley 1982). Courier Dover Publications. صفحة 82. ISBN 978-0-486-67620-3. مؤرشف من الأصل في 20 مارس 2015. الوسيط |CitationClass= تم تجاهله (مساعدة)
Gerald B Folland. Fourier Analysis and its Applications. صفحة 77ff. الوسيط |CitationClass= تم تجاهله (مساعدة)
Peter J. (2013-11-08). Introduction to Partial Differential Equations (باللغة الإنجليزية). Springer Science & Business Media. ISBN 978-3-319-02099-0. مؤرشف من الأصل في 12 أبريل 2020. الوسيط |CitationClass= تم تجاهله (مساعدة)
Lawrence (2013-09-25). Advanced Engineering Mathematics (باللغة الإنجليزية). CRC Press. ISBN 978-1-4398-3447-3. مؤرشف من الأصل في 12 أبريل 2020. الوسيط |CitationClass= تم تجاهله (مساعدة)
"Parametric Equation of a Circle - Math Open Reference". www.mathopenref.com. مؤرشف من الأصل في 18 نوفمبر 2019. اطلع عليه بتاريخ 25 مايو 2020. الوسيط |CitationClass= تم تجاهله (مساعدة)
"Welcome to CK-12 Foundation | CK-12 Foundation". www.ck12.org. مؤرشف من الأصل في 17 فبراير 2017. اطلع عليه بتاريخ 25 مايو 2020. الوسيط |CitationClass= تم تجاهله (مساعدة)
Weisstein, Eric W. "Lissajous Curve". mathworld.wolfram.com (باللغة الإنجليزية). مؤرشف من الأصل في 15 نوفمبر 2019. اطلع عليه بتاريخ 25 مايو 2020. الوسيط |CitationClass= تم تجاهله (مساعدة)
Francis A.; White, Harvey E. (1937). Fundamentals of Optics (باللغة الإنجليزية). Tata McGraw-Hill Education. ISBN 978-1-259-00229-8. مؤرشف من الأصل في 24 فبراير 2020. الوسيط |CitationClass= تم تجاهله (مساعدة)
Vasiliĭ Petrovich (1963). Navigation Instruments (باللغة الإنجليزية). Foreign Technology Division. مؤرشف من الأصل في 24 فبراير 2020. الوسيط |CitationClass= تم تجاهله (مساعدة)
Halliday, Resnick and Krane ,Physics
"Parametric Equations and Projectile Motion" (PDF). Classzone. مؤرشف من الأصل (PDF) في 12 أبريل 2020. الوسيط |CitationClass= تم تجاهله (مساعدة); line feed character في |عنوان= على وضع 25 (مساعدة)
"Contemporary Physics". مؤرشف من الأصل في 22 أبريل 2020. الوسيط |CitationClass= تم تجاهله (مساعدة)
King 1986، صفحة 83.
الصيغة التي تكافئها موجودة في Hadi Bashori 2015، صفحة 119
Hadi Bashori 2015، صفحة 119.
Mark (2009-12-03). Professional English in Use Engineering with Answers: Technical English for Professionals (باللغة الإنجليزية). Cambridge University Press. ISBN 978-0-521-73488-2. مؤرشف من الأصل في 12 مارس 2020. الوسيط |CitationClass= تم تجاهله (مساعدة)
بررسی سیستم‌های قدرت (باللغة الفارسية). طهران. ISBN 964-454-394-7. الوسيط |CitationClass= تم تجاهله (مساعدة)
"Electrical Power in AC Circuits and Reactive Power". مؤرشف من الأصل في 12 يوليو 2019. الوسيط |CitationClass= تم تجاهله (مساعدة)
Alan V.; Willsky, Alan S.; Nawab, Syed Hamid (1997). Signals & Systems (باللغة الإنجليزية). Prentice-Hall International. ISBN 978-0-13-651175-5. مؤرشف من الأصل في 12 أبريل 2020. الوسيط |CitationClass= تم تجاهله (مساعدة)

معلومات الكتب كاملة

Abramowitz, Milton; Stegun, Irene Ann (1983). Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables ^{[الإنجليزية]}. ISBN 978-0-486-61272-0. الوسيط |CitationClass= تم تجاهله (مساعدة)
Lars Ahlfors (1966). Complex Analysis: an introduction to the theory of analytic functions of one complex variable (الطبعة الثانية). New York: McGraw-Hill Education. ISBN 0-471-54397-7. الوسيط |CitationClass= تم تجاهله (مساعدة)
Boyer, Carl B. (1991). A History of Mathematics (الطبعة الثانية). John Wiley & Sons, Inc. ISBN 0-471-54397-7. الوسيط |CitationClass= تم تجاهله (مساعدة)
Gal, Shmuel; Bachelis, Boris (1991). An accurate elementary mathematical library for the IEEE floating point standard, ACM Transactions on Mathematical Software. الوسيط |CitationClass= تم تجاهله (مساعدة)
Joseph, George G (2000). The Crest of the Peacock: Non-European Roots of Mathematics (الطبعة الثانية). London: Penguin Books. ISBN 0-691-00659-8. الوسيط |CitationClass= تم تجاهله (مساعدة)
Kantabutra, Vitit (1996). "On hardware for computing exponential and trigonometric functions". IEEE Trans. Computers. IEEE: 328–339. الوسيط |CitationClass= تم تجاهله (مساعدة)
Maor, Eli. Trigonometric Delights (الطبعة 1998). Princeton Univ. Press. ISBN 0-691-09541-8. الوسيط |CitationClass= تم تجاهله (مساعدة)
Needham, Tristan (1999). Preface to Visual Complex Analysis (PDF). Oxford University Press. ISBN 0-19-853446-9. الوسيط |CitationClass= تم تجاهله (مساعدة)
Nielsen, Kaj L. (1966). "Logarithmic and Trigonometric Tables to Five Places" (الطبعة الثانية). New York, USA: Barnes & Noble. LCCN 61-9103. الوسيط |CitationClass= تم تجاهله (مساعدة); Cite journal requires |journal= (مساعدة)
O'Connor, J. J.; E. F. Robertson (1996). Trigonometric functions. MacTutor History of Mathematics archive. الوسيط |CitationClass= تم تجاهله (مساعدة)
O'Connor, J. J; E. F. Robertson (2000). Madhava of Sangamagramma. MacTutor History of Mathematics archive. مؤرشف من الأصل في 25 أغسطس 2019. الوسيط |CitationClass= تم تجاهله (مساعدة)
Pearce, Ian G (2002). Madhava of Sangamagramma. MacTutor History of Mathematics archive. مؤرشف من الأصل في 02 يوليو 2019. الوسيط |CitationClass= تم تجاهله (مساعدة)
Protter, Murray H; Morrey, Charles B., Jr (1970). "College Calculus with Analytic Geometry" (الطبعة الثانية). Reading: Addison-Wesley. LCCN 76087042. الوسيط |CitationClass= تم تجاهله (مساعدة); Cite journal requires |journal= (مساعدة)
Weisstein, Eric W. Tangent. from MathWorld. مؤرشف من الأصل في 30 ديسمبر 2019. اطلع عليه بتاريخ 21 يناير 2006. الوسيط |CitationClass= تم تجاهله (مساعدة); غير مسموح بالترميز المائل أو الغامق في: |ناشر= (مساعدة)
Gerald B; Folland (2009). "Convergence and completeness". Fourier Analysis and its Applications (باللغة الإنجليزية). American Mathematical Society. ISBN 978-0-8218-4790-9. مؤرشف من الأصل في 12 أبريل 2020. الوسيط |CitationClass= تم تجاهله (مساعدة)

ملحق: مسرد المصطلحات الإنجليزية

مَسرد المفردات وفق الترتيب الأبجدي الإنجليزي
A
إحداثي x	Abscissa
قدرة فعالة	Active power
زاوية حادة	Acute angle
إضافة	Addition
ضلع مجاور	Adjacent side
عدد جبري	Algebraic number
تيار متناوب	Alternating current
مطال موجة	Amplitude of a wave
تضمين المطال	Amplitude modulation
إشارة تشابهية	Analog signal
زاوية	Angle
متطابقات مجموع وفرق زاويتين	Angle sum and difference identities
تردد زاوي	Angular frequency
زخم زاوي	Angular momentum
مشتق عكسي	Antiderivative
تقريب	Approximation
قوس	Arc
مساحة	Area
عُمدة	Argument
متوسط حسابي هندسي	Arithmetic–geometric mean
B
عدد بيرنولي	Bernoulli number
دالة بيسل	Bessel function
دالة تقابلية	Bijective function
C
حساب التفاضل والتكامل	Calculus
موجة حاملة	Carrier wave
معادلة مميزة	Characteristic equation
تقريب تشيبيشيف	Chebyshev approximation
متعدد الحدود لشيبيشيف	Chebyshev polynomial
دالة الوتر	Chord
زاوية دائرية	Circular angle
حركة دائرية	Circular motion
قطاع دائري	Circular sector
محيط دائرة/قطع ناقص (منحنى مغلق بشكل عام)	Circumference
مضلع محيط	Circumscribed polygon
مستقر دالة	Codomain of a function
تصادم	Collision
قناة اتصال	Communication Channel
فرجار	Compass
زوايا متتامة	Complementary angles
تحليل مركب/عقدي	Complex analysis
عدد مركب/عقدي	Complex number
مستوي مركب/عقدي	Complex plane
دالة مستمرة	Continuous function
إحداثيات	Coordinates
لازمة	Corollary
جداء متجهي/ضرب متجهي	Cross product
جذر تكعيبي	Cube root
سهم التمام	Coversine
رباعي دائري	Cyclic quadrilateral
إحداثيات أسطوانية	Cylindrical coordinates
D
صيغة دي موافر	De Moivre's formula
درجة	Degree
مقام	Denominator
مشتق	Derivative
قطر الدائرة	Diameter
فرق	Difference
تفاضل	Differential
معادلة تفاضلية	Differential equation
دالة ديراك	Dirac function
تيار مستمر	Direct Current
متطابقات ضعف الزاوية	Double-angle identities
مجال دالة	Domain of a function
جداء قياسي	Dot product
E
تباعد مركزي	Eccentricity
أحرف متعدد السطوح	Edges of a polyhedron
دالة ذاتية	Eigenfunction
قطع ناقص/إهليلج	Ellipse
تكامل اهليلجي	Elliptic integral
دالة كاملة	Entire function
معادلة حركة	Equation of motion
مثلث متساوي الأضلاع	Equilateral triangle
متطابقة أويلر	Euler's identity
عدد أويلر	Euler number
دوال زوجية وفردية	Even and odd functions
قاطع التمام الخارجي	Excosecant
قاطع خارجي	Exsecant
دالة أسية	Exponential function
F
عاملي عدد	Factorial of a number
وحدة الفاصلة العائمة	Floating Point Unit
متسلسلة فورييه	Fourier series
تحويل فورييه	Fourier transform
G
نظرية غالوا	Galois theory
كسر مستمر معمم	Generalized continued fraction
تشابه هندسي	Geometric similarity
تمثيل بياني لدالة	Graph of a function
تسارع الجاذبية	Gravitational acceleration
H
متطابقات نصف الزاوية	Half-angle identities
مضاعف العتاد	Hardware multiplier
نصف السهم	Haversine
لولب	Helix
المعالِجات الراقية	Higher-end Processors
دالة تامة الشكل	Holomorphic function
قطع زائد	Hyperbola
زاوية زائدية	Hyperbolic angle
دوال زائدية	Hyperbolic functions
قطاع زائدي	Hyperbolic sector
وتر المثلث	Hypotenuse
منحنى عجلي تحتي	Hypotrochoid
I
وحدة تخيلية	Imaginary unit
متباينة	Inequality
دالة متباينة	Injective function
مضلع محاط	Inscribed polygon
تكامل	Integral
عدد صحيح	Integer number
مجال/فترة	Interval
تقاطع مستقيمين	Intersection of two lines
متسلسلة الجداء اللانهائي	Infinite product expansion
قدرة لحظية	Instantaneous power
دالة عكسية	Inverse function
نقطة معزولة	Isolated point
L
تحويل لابلاس	Laplace transform
مؤثر لابلاسي	Laplace operator / Laplacian
قانون جيب التمام	Law of cosines
قانون حفظ الزخم	Law of momentum conservation
قانون الجيب	Law of sines
ساق مثلث	Leg of a triangle
طول	Length
نهاية دالة	Limit of a function
مستقيم	Line
منحنى ليساجو	Lissajous curve
M
متسلسلة ماكلورين	Maclaurin series
مقدار	Magnitude
معيار عدد مركب	Magnitude of a complex number
إسقاط الخرائط	Map projection
دالة جزئية الشكل	Meromorphic function
تضمين	Modulation
صيغة مولفيده	Mollweide's formula
زخم	Momentum
دالة رتيبة	Monotonic function
قانون موري	Morrie's law
دالة متعددة القيم	Multivalued function
N
مقابل عدد	Negative of a number
بسط	Numerator
جذر نوني	nth root
O
ضلع مقابل	Opposite side
إحداثي y	Ordinate
نقطة الأصل	Origin
دوال متعامدة	Orthogonal functions
P
تقريب بادي	Padé approximant
متوازي السطوح	Parallelepiped
متوازي أضلاع	Parallelogram
معادلة وسيطية	Parametric equation
جسم / جسيم	Particle
حركة رقاصية/حركة بندولية	Pendular motion
محيط (مضلعات)	Perimeter
دالة دورية	Periodic function
دورية	Periodicity
طور	Phase
تقدم وتأخر الطور	Phase leading and lagging
إحداثيات قطبية	Polar coordinates
زاوية القدرة	Power angle
معامل القدرة	Power factor
متسلسلة قوى	Power series / Power expansion
مبرهنة بطليموس	Ptolemy's theorem
متطابقة فيثاغورس	Pythagorean identity
مبرهنة فيثاغورس	Pythagorean theorem
Q
ربع الدائرة	Quadrant
قاعدة ناتج القسمة	Quotient rule
R
نسبة	Ratio
نصف القطر	Radius
نصف قطر التقارب	Radius of convergence
تقليص المدى	Range reduction
سرعة التقارب	Rate of convergence
دالة كسرية	Rational function
عدد كسري/نسبي/ناطق/جذري	Rational number
قدرة غير فعالة	Reactive power
عدد حقيقي	Real number
علاقة استدعاء ذاتي	Recurrence relation
إنعكاس	Reflection
انكسار الضوء	Refraction of light
خماسي منتظم	Regular pentagon
باقي (متسلسلة)	Remainder term
زاوية قائمة	Right angle
مثلث قائم الزاوية	Right-angled triangle / Right triangle
جذر معادلة/جذر دالة	Root
دوران	Rotation
S
عمق القوس	Sagitta
موجة سن المنشار	Sawtooth wave
نصف المحور الأكبر	Semi-major axis
نصف المحور الأصغر	Semi-minor axis
مجموعة القيم الرئيسية	Set of principal values
حركة توافقية بسيطة	Simple Harmonic Motion
موجة جيبية	Sine wave
قانون سنيل	Snell's law
حل المثلثات	Solution of triangles
زوايا خاصة	Special angles
دوال خاصة	Special functions
إحداثيات كروية	Spherical coordinates
مثلث كروي	Spherical triangle
حساب المثلثات الكروية	Spherical trigonometry
نابض	Spring
جذر تربيعي	Square root
موجة مربعية	Square wave
مبرهنة الساندويتش	Squeeze theorem / Sandwich theorem
مسطرة	Straightedge
طرح	Subtraction
مجموع	Sum
تناظر/تماثل	Symmetry
T
مماس	Tangent
تعويض بظل نصف الزاوية	Tangent half-angle substitution
متسلسلة تايلور	Taylor series
حدود	Terms
مبرهنة طاليس	Thales theorem
تيارات ثلاثية الطور	Three-phase current
عدد متسامي	Transcendental numbers
مسح اجتيازي	Traverse
تثليث	Triangulation
علم المثلثات/حساب المثلثات	Trigonometry
متطابقات ثلاثية الزاوية	Triple-angle identities
دورة (وحدة قياس الزوايا)	Turn
U
دائرة الوحدة	Unit circle
V
متجه	Vector
سهم/ جيب منكوس	Versine
W
تعويض فايرشتراس	Weierstrass substitution
X
محور السينات	x-axis
Y
محور الصادات	y-axis
3
قياس بصري ثلاثي الأبعاد	3D Optical measurement

وصلات خارجية

كتاب عن حساب المثلثات ترجمهُ محمد أفندي دقله من الفرنسية إلى العربية بمدرسة المهندسخانة الخديوية المصرية (يعود هذا الكتاب لفترة محمد علي باشا)، المكتبة الوطنية النمساوية.
Visionlearning Module on Wave Mathematics (بالإنجليزية)
الدوال المثلثية والدوال المثلثية العكسية (PDF) (بالعربية)
استعمالات الدوال المثلثية في الهندسة الكهربائية (PDF) (بالعربية)
إنشاء زاوية بالفرجار (بدون منقلة) (بالعربية)

بوابة رياضيات
بوابة تحليل رياضي
بوابة هندسة رياضية

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.

[:0-7] وقد يُشار إليها أيضاً بـ ${\text{tg}}$ .

[:1-8] تُسمّى أيضاً دائرة مثلثية أو دائرة واحدية.

[15] حيث k عدد صحيح كيفي.

[17] أو تلك الرموز: cotan, cotg ctg, ctn

[18] أو هذا الرمز: cosec

[19] تم تدوين الشكل الانجليزي لأول مرة عام 1593 في الكتاب Horologiographia الخاص بـ Thomas Fale.

[20] هناك مصادر مختلفة أنسبت الاستخدام الاول للمصطلح "sinus" إلى:
إما ترجمة أفلاطون تيبورتينوس في عام 1116 لأعمال البتاني الخاصة بعلم الفلك.

أو ترجمة جيراردو الكريموني لجبر الخوارزمي

أو ترجمة روبرت أوف تشستر سنة 1145 لجداول الخوارزمي

طالع:‏
‏Merlet, A Note on the History of the Trigonometric Functions in Ceccarelli (ed.), International Symposium on History of Machines and Mechanisms, Springer, 2004

أو‏
‏Maor (1998), chapter 3, for an earlier etymology crediting Gerard.

أو‏
‏Katx, Victor (July 2008). A history of mathematics (باللغة الإنجليزية) (الطبعة 3). Boston: Pearson. صفحة 210 (sidebar). ISBN 978-0321387004. الوسيط |CitationClass= تم تجاهله (مساعدة)

[8] إما ترجمة أفلاطون تيبورتينوس في عام 1116 لأعمال البتاني الخاصة بعلم الفلك.

[9] أو ترجمة جيراردو الكريموني لجبر الخوارزمي

[10] أو ترجمة روبرت أوف تشستر سنة 1145 لجداول الخوارزمي

[11] طالع:‏
‏Merlet, A Note on the History of the Trigonometric Functions in Ceccarelli (ed.), International Symposium on History of Machines and Mechanisms, Springer, 2004

[12] أو‏
‏Maor (1998), chapter 3, for an earlier etymology crediting Gerard.

[13] أو‏
‏Katx, Victor (July 2008). A history of mathematics (باللغة الإنجليزية) (الطبعة 3). Boston: Pearson. صفحة 210 (sidebar). ISBN 978-0321387004. الوسيط |CitationClass= تم تجاهله (مساعدة)

[:6-26] طالع فرع من قسم التاريخ "العصر الذهبي للحضارة الإسلامية" لمزيد من التفاصيل.

[38] كانت العلاقة المثلثية لدالة الظل معروفة عند الهنود، ولكن لم يعتبروها كميةً مثلثيةً مستقلة كدالة الجيب.

[:4-72] الشريط الأفقي فوق الرقم يعني أن هذا الرقم يتكرر إلى ما لا نهاية.

[75] المثلث القائم أو المثلث قائم الزاوية هو مثلثٌ إحدى زواياه قائمة، أي أن ضلعيه يشكلان زاوية قياسها $90^{\circ }$ .

[:3-77] يسمى أيضًا محور الفواصل أو محور الأفاصيل

[81] عكس اتجاه عقارب الساعة لأجلِ زاويةٍ موجبةٍ $\theta >0$ ، وفي اتجاه عقارب الساعة من أجل زاويةٍ سالبةٍ $\theta <0$ .

[مولد_تلقائيا11-82] يُسمّى أيضاً الفاصلة أو الأفصول.

[مولد_تلقائيا10-83] يُسمّى أيضاً الترتيبة أو الأرتوب.

[84] يسمى أيضًا محور العينات (في سوريا) أو محور التراتيب أو محور الأراتيب

[104] نصف قطر التقارب لمتسلسلة قوى هو نصف قطر أكبر قرص تتقارب فيه المتسلسلة. وهو إما عدد حقيقي غير سالب أو ∞.

[114] المعادلة الدالية هي أي معادلة التي متغيرها هي عبارة عن دالة.

[118] تكون الدوال متعامدة إذا كان جدائهما الداخلي يساوي الصفر.

[121] حيث: a هو ثابت حقيقي. s هو عدد مركب.

[123] حيث:
$\omega$ هي السرعة الزاوية.

$\delta (\cdot )$ هي دالة ديراك.
$i$ هي وحدة تخيلية مربعها يساوي -1.

[28] $\omega$ هي السرعة الزاوية.

[29] $\delta (\cdot )$ هي دالة ديراك.

[:2-134] أطوال الأضلاع تساوي عدديًا قياس الزوايا التي تقابل أقواس الدائرة العظمى في المركز بالراديان. لذلك، بالنسبة لكرة ذات نصف قطر R لا يساوي الواحد، يجب قسمة أطوال الأضلاع على R قبل استخدام المتطابقة.

[152] هي وحدة تخيلية مربعها يساوي -1

[155] تسمى أيضًا "أشعة" مفردها "شعاع".

[156] وتسمى أيضا "جداء سلمي".

[158] تسمى أيضا "ضرب اتجاهي" أو "جداء شعاعي"

[162] عامد هو قطعة مستقيمة التي تربط مركز المضلع المنتظم بمنتصف أحد أضلاعه

[170] المسح الاجتيازي هو طريقة لمسح منطقة مفتوحة أو مغلقة باستخدام قياس الزوايا والمسافات.

[:5-188] يجب تحويل الإحداثيات إلى الراديان في الحساب.

[196] إذا كان إحداثي خط العرض معبر عنه بالدرجات العشرية متبوع بـ N (التي تعني شمالاً)، يجب وضع إشارة "+" قبل قيمة خط العرض؛ وإذا كان متبوع بـ S (التي تعني جنوبًا)، نضع إشارة "-" قبل القيمة.

بنفس الطريقة المذكورة أعلاه، إذا كان احداثي خط الطول بالدرجات العشرية متبوع بـ E (التي تعني شرقًا)، يجب وضع إشارة "+" قبل قيمة خط الطول؛ وإذا كان متبوع بـ W (التي تعني غربًا)، نضع إشارة "-" قبل القيمة.

وإن كانت الإحداثيات معبر عنها بالدرجات والدقائق والثواني، يجب تحويلها إلى الدرجات العشرية، طالع قسم وحدات قياس الزوايا.

[39] إذا كان إحداثي خط العرض معبر عنه بالدرجات العشرية متبوع بـ N (التي تعني شمالاً)، يجب وضع إشارة "+" قبل قيمة خط العرض؛ وإذا كان متبوع بـ S (التي تعني جنوبًا)، نضع إشارة "-" قبل القيمة.

[40] بنفس الطريقة المذكورة أعلاه، إذا كان احداثي خط الطول بالدرجات العشرية متبوع بـ E (التي تعني شرقًا)، يجب وضع إشارة "+" قبل قيمة خط الطول؛ وإذا كان متبوع بـ W (التي تعني غربًا)، نضع إشارة "-" قبل القيمة.

[41] وإن كانت الإحداثيات معبر عنها بالدرجات والدقائق والثواني، يجب تحويلها إلى الدرجات العشرية، طالع قسم وحدات قياس الزوايا.

[199] حيث:
$i$ هي دالة التيار الكهربائي

$v$ هي دالة الجهد الكهربائي

$V_{m}$ و $I_{m}$ هما مطالا دالة التيار الكهربائي ودالة الجهد الكهربائي.

$\omega$ هو التردد الزاوي.

$\theta$ هو الطور الابتدائي.

[43] $i$ هي دالة التيار الكهربائي

[44] $v$ هي دالة الجهد الكهربائي

[45] $V_{m}$ و $I_{m}$ هما مطالا دالة التيار الكهربائي ودالة الجهد الكهربائي.

[46] $\omega$ هو التردد الزاوي.

[47] $\theta$ هو الطور الابتدائي.

[:42-1] د فرانك; موير, د روبرت (2004-03-01). سلسلة ملخصات شوم ايزي ; حساب المثلثات. international house for cultural investments. ISBN 978-977-282-145-7. مؤرشف من الأصل في 21 فبراير 2020. الوسيط |CitationClass= تم تجاهله (مساعدة)

[2] محمد مفيد (2013-01-01). التكامل في الرياضات. مركز الكتاب الأكاديمي. ISBN 978-9957-35-052-9. مؤرشف من الأصل في 21 فبراير 2020. الوسيط |CitationClass= تم تجاهله (مساعدة)

[:5-3] ميشال إبراهيم ورامي أبو سليمان وفادي (2007-01-01). قاموس المصطلحات العلمية - انكليزي/فرنسي/عربي. دار الكتب العلمية. ISBN 978-2-7451-5445-3. مؤرشف من الأصل في 21 فبراير 2020. الوسيط |CitationClass= تم تجاهله (مساعدة)

[4] Katx, Victor (July 2008). A history of mathematics (باللغة الإنجليزية) (الطبعة 3). Boston: Pearson. صفحة 210 (sidebar). ISBN 978-0321387004. الوسيط |CitationClass= تم تجاهله (مساعدة)

[:52-5] "Clark University". مؤرشف من الأصل في 18 ديسمبر 2017. الوسيط |CitationClass= تم تجاهله (مساعدة)

[6] A Note on the History of the Trigonometric Functions in Ceccarelli (ed.), International Symposium on History of Machines and Mechanisms, Springer, 2004 See Maor (1998), chapter 3, for an earlier etymology crediting Gerard. See Katx, Victor (July 2008). A history of mathematics (باللغة الإنجليزية) (الطبعة 3). Boston: Pearson. صفحة 210 (sidebar). ISBN 978-0321387004. الوسيط |CitationClass= تم تجاهله (مساعدة) نسخة محفوظة 10 يونيو 2018 على موقع واي باك مشين.

[:3-9] كرلو (199?). علم الفلك. ktab INC. مؤرشف من الأصل في 12 أبريل 2020. الوسيط |CitationClass= تم تجاهله (مساعدة); تحقق من التاريخ في: |تاريخ= (مساعدة)

[10] "5 معلومات مهمة عن المثلث وزوايا المثلث". إيد أرابيا. 2018-10-15. مؤرشف من الأصل في 22 ديسمبر 2019. اطلع عليه بتاريخ 12 أبريل 2020. الوسيط |CitationClass= تم تجاهله (مساعدة)

[11] الرياضيات - المنهاج الجزائري القديم. 1999. الوسيط |CitationClass= تم تجاهله (مساعدة)

[12] Max; Association, Research and Education (1984-01-01). Handbook of Mathematical, Scientific, and Engineering Formulas, Tables, Functions, Graphs, Transforms (باللغة الإنجليزية). Research & Education Assoc. ISBN 978-0-87891-521-7. مؤرشف من الأصل في 13 أبريل 2020. الوسيط |CitationClass= تم تجاهله (مساعدة)

[:15-13] Anthony (2007). Pure mathematics: Trigonometry (باللغة الإنجليزية). Pass Publications. ISBN 978-1-872684-87-1. مؤرشف من الأصل في 13 أبريل 2020. الوسيط |CitationClass= تم تجاهله (مساعدة)

[مولد_تلقائيا5-14] Journal of Engineering for Industry (باللغة الإنجليزية). American Society of Mechanical Engineers. 1969. مؤرشف من الأصل في 13 أبريل 2020. الوسيط |CitationClass= تم تجاهله (مساعدة)

[:9-16] "Table of Domain and Range of Common Functions". www.analyzemath.com. مؤرشف من الأصل في 8 فبراير 2019. اطلع عليه بتاريخ 10 أبريل 2020. الوسيط |CitationClass= تم تجاهله (مساعدة)

[مولد_تلقائيا3-21] Kim (2008-12-29). Mathematics in India (باللغة الإنجليزية). Princeton University Press. ISBN 978-1-4008-3407-5. مؤرشف من الأصل في 04 مارس 2020. الوسيط |CitationClass= تم تجاهله (مساعدة)

[22] القانون المسعودي. 1. صفحة 275. الوسيط |CitationClass= تم تجاهله (مساعدة)

[23] أبي الفتح إسماعيل بن مصطفى/شيخ زاده (2019-01-01). رسائل الكلنبوي في علم الفلك - رسالة الربع المجيب. دار الكتب العلمية. صفحة 151. ISBN 978-2-7451-8540-2. مؤرشف من الأصل في 1 يوليو 2020. الوسيط |CitationClass= تم تجاهله (مساعدة)

[مولد_تلقائيا2-24] Oxford English Dictionary

[مولد_تلقائيا16-25] Régis (1996). Encyclopedia of the History of Arabic Science (باللغة الإنجليزية). Psychology Press. ISBN 978-0-415-12411-9. مؤرشف من الأصل في 04 مارس 2020. الوسيط |CitationClass= تم تجاهله (مساعدة)

[Gunter_1620-27] Gunter, Edmund (1620). Canon triangulorum. الوسيط |CitationClass= تم تجاهله (مساعدة)

[Datta-28] B.B. Datta and A.N. Singh (1983). "Hindu Trigonometry" (PDF). Indian Journal of History of Science. 18 (1): 39–108. مؤرشف من الأصل (PDF) في 05 فبراير 2017. اطلع عليه بتاريخ 01 مارس 2010. الوسيط |CitationClass= تم تجاهله (مساعدة)

[29] Team, Almaany. "تعريف و شرح و معنى تمام بالعربي في معاجم اللغة العربية معجم المعاني الجامع، المعجم الوسيط ،اللغة العربية المعاصرة ،الرائد ،لسان العرب ،القاموس المحيط - معجم عربي عربي صفحة 1". www.almaany.com (باللغة الإنجليزية). مؤرشف من الأصل في 22 أغسطس 2016. اطلع عليه بتاريخ 10 أبريل 2020. الوسيط |CitationClass= تم تجاهله (مساعدة)

[30] Steven G. (2010-04). An Episodic History of Mathematics: Mathematical Culture Through Problem Solving (باللغة الإنجليزية). MAA. ISBN 978-0-88385-766-3. مؤرشف من الأصل في 20 يونيو 2020. الوسيط |CitationClass= تم تجاهله (مساعدة); تحقق من التاريخ في: |تاريخ= (مساعدة)

[31] Howard (1983). Great Moments in Mathematics (before 1650) (باللغة الإنجليزية). MAA. ISBN 978-0-88385-310-8. مؤرشف من الأصل في 20 يونيو 2020. الوسيط |CitationClass= تم تجاهله (مساعدة)

[32] Tobias (2012-10-02). Mathematics in Ancient Greece (باللغة الإنجليزية). Courier Corporation. ISBN 978-0-486-14998-1. مؤرشف من الأصل في 15 أبريل 2020. الوسيط |CitationClass= تم تجاهله (مساعدة)

[Boyer_19912-33] Boyer, Carl B. (1991). A History of Mathematics (Second ed.). John Wiley & Sons, Inc. (ردمك 0-471-54397-7).

[toomer-34] Toomer, G. (1998), Ptolemy's Almagest, Princeton University Press, ISBN 978-0-691-00260-6 الوسيط |CitationClass= تم تجاهله (مساعدة); الوسيط |separator= تم تجاهله (مساعدة)CS1 maint: ref=harv (link)

[35] موسوعة تاريخ العلوم العربية - ثلاثة مجلدات. مؤرشف من الأصل في 12 أكتوبر 2016. الوسيط |CitationClass= تم تجاهله (مساعدة)

[mact-biog2-36] O'Connor; Robertson. "Madhava of Sangamagrama". School of Mathematics and Statistics University of St Andrews, Scotland. مؤرشف من الأصل في 14 مايو 2006. اطلع عليه بتاريخ 08 سبتمبر 2007. الوسيط |CitationClass= تم تجاهله (مساعدة)

[Gingerich_1986-37] Gingerich, Owen (1986). "Islamic Astronomy". ساينتفك أمريكان. المجلد. 254. صفحة 74. مؤرشف من الأصل في 19 أكتوبر 2013. اطلع عليه بتاريخ 13 يوليو 2010. الوسيط |CitationClass= تم تجاهله (مساعدة)

[39] "History of Trigonometry - Part 3". nrich.maths.org. مؤرشف من الأصل في 20 فبراير 2020. اطلع عليه بتاريخ 05 أبريل 2020. الوسيط |CitationClass= تم تجاهله (مساعدة)

[Sesiano-40] Jacques Sesiano, "Islamic mathematics", p. 157, in Selin, Helaine; D'Ambrosio, Ubiratan, المحررون (2000). Mathematics Across Cultures: The History of Non-western Mathematics. Springer. ISBN 1-4020-0260-2. الوسيط |CitationClass= تم تجاهله (مساعدة)

[Britannica-41] "trigonometry". Encyclopedia Britannica. مؤرشف من الأصل في 12 مايو 2015. الوسيط |CitationClass= تم تجاهله (مساعدة)

[42] أبو الريحان البيروني (2002-01-01). القانون المسعودي 1-3 ج1. دار الكتب العلمية. صفحة 225. ISBN 978-2-7451-3305-2. مؤرشف من الأصل في 22 يونيو 2020. الوسيط |CitationClass= تم تجاهله (مساعدة)

[43] Adolph P. Yushkevich. История математики. С древнейших времен до начала Нового времени (باللغة الروسية). الوسيط |CitationClass= تم تجاهله (مساعدة)

[44] مجلة تاريخ العلوم العربية (باللغة الإنجليزية). Institute for the History of Arabic Science, University of Aleppo. 1977. مؤرشف من الأصل في 20 يونيو 2020. الوسيط |CitationClass= تم تجاهله (مساعدة)

[45] إبراهيم (2002-01-01). دليل الأوائل. ktab INC. مؤرشف من الأصل في 20 يونيو 2020. الوسيط |CitationClass= تم تجاهله (مساعدة)

[46] المعلم الجديد. المجلد 30. الوسيط |CitationClass= تم تجاهله (مساعدة)

[47] Florian (1898). A History of Elementary Mathematics (باللغة الإنجليزية). Macmillan. الوسيط |CitationClass= تم تجاهله (مساعدة)

[48] Ravi P.; Sen, Syamal K. (2014-11-11). Creators of Mathematical and Computational Sciences (باللغة الإنجليزية). Springer. ISBN 978-3-319-10870-4. مؤرشف من الأصل في 18 مايو 2020. الوسيط |CitationClass= تم تجاهله (مساعدة)

[49] مصطفى (2005-01-01). موسوعة علماء العرب والمسلمين وأعلامهم. Al Manhal. ISBN 9796500011424. مؤرشف من الأصل في 12 أبريل 2020. الوسيط |CitationClass= تم تجاهله (مساعدة)

[:4-50] Dirk Jan (1967). A Concise History of Mathematics (باللغة الإنجليزية). Courier Corporation. ISBN 978-0-486-60255-4. مؤرشف من الأصل في 03 مارس 2020. الوسيط |CitationClass= تم تجاهله (مساعدة)

[51] Donald Routledge Hill (1996), "Engineering", in Roshdi Rashed, Encyclopedia of the History of Arabic Science, Vol. 3, p. 751–795 [769].

[52] O'Connor, John J.; Robertson, Edmund F., "Abu Arrayhan Muhammad ibn Ahmad al-Biruni", تاريخ ماكتوتور لأرشيف الرياضيات الوسيط |CitationClass= تم تجاهله (مساعدة); الوسيط |separator= تم تجاهله (مساعدة)CS1 maint: ref=harv (link)

[مولد_تلقائيا17-53] Elias C.; Tonias, Constantine N. (2016-04-28). Geometric Procedures for Civil Engineers (باللغة الإنجليزية). Springer. ISBN 978-3-319-24295-8. مؤرشف من الأصل في 21 يونيو 2020. الوسيط |CitationClass= تم تجاهله (مساعدة)

[مولد_تلقائيا12-54] نوال حسن; الخليج, دار (2017-01-01). العلوم عند العرب والمسلمين. دار الخليج للنشر والتوزيع / daralkhalij for Publishing and Distribution. ISBN 978-9957-519-85-8. مؤرشف من الأصل في 12 أبريل 2020. الوسيط |CitationClass= تم تجاهله (مساعدة)

[55] Clifford A. (2009). The Math Book: From Pythagoras to the 57th Dimension, 250 Milestones in the History of Mathematics (باللغة الإنجليزية). Sterling Publishing Company, Inc. ISBN 978-1-4027-5796-9. مؤرشف من الأصل في 15 مايو 2020. الوسيط |CitationClass= تم تجاهله (مساعدة)

[56] قرقور, يوسف. "ملك سرقسطة المؤتمن بن هود ومبرهنة فيثاغورس: مصادرها وامتداداتها" (PDF). ISSN 0210-8615. مؤرشف من الأصل (PDF) في 29 يونيو 2017. الوسيط |CitationClass= تم تجاهله (مساعدة); Cite journal requires |journal= (مساعدة)

[57] Marlow Anderson, Victor J. Katz, Robin J. Wilson (2004), Sherlock Holmes in Babylon and Other Tales of Mathematical History, جمعية الرياضيات الأمريكية, صفحة 139, ISBN 0883855461 الوسيط |CitationClass= تم تجاهله (مساعدة); الوسيط |separator= تم تجاهله (مساعدة)CS1 maint: ref=harv (link)

[58] George Gheverghese (2011). The Crest of the Peacock: Non-European Roots of Mathematics (Third Edition) (باللغة الإنجليزية). Princeton University Press. ISBN 978-0-691-13526-7. الوسيط |CitationClass= تم تجاهله (مساعدة)

[katz_308-59] Katz 2007، p. 308

[MacTutor-60] O'Connor, John J.; Robertson, Edmund F., "دوال مثلثية", تاريخ ماكتوتور لأرشيف الرياضيات الوسيط |CitationClass= تم تجاهله (مساعدة); الوسيط |separator= تم تجاهله (مساعدة)CS1 maint: ref=harv (link)

[61] Carl B. (2012-10-09). The History of the Calculus and Its Conceptual Development (باللغة الإنجليزية). Courier Corporation. ISBN 978-0-486-17538-6. مؤرشف من الأصل في 12 أبريل 2020. الوسيط |CitationClass= تم تجاهله (مساعدة)

[Fincke-62] "Fincke biography". مؤرشف من الأصل في 07 يناير 2017. اطلع عليه بتاريخ 15 مارس 2017. الوسيط |CitationClass= تم تجاهله (مساعدة)

[Bourbaki_1994-63] Bourbaki, Nicolás (1994). Elements of the History of Mathematics. Springer. مؤرشف من الأصل في 16 فبراير 2020. الوسيط |CitationClass= تم تجاهله (مساعدة)

[64] Robert E. Bradley, Lawrence A. D'Antonio, Charles Edward Sandifer. Euler at 300: an appreciation. Mathematical Association of America, 2007. Page 100.

[65] أبو الريحان البيروني. القانون المسعودي. 1. صفحة 321. الوسيط |CitationClass= تم تجاهله (مساعدة)

[66] Nielsen (1966, pp. xxiii–xxiv)

[67] Glen Van (2020-01-23). Trigonometry: a Very Short Introduction (باللغة الإنجليزية). Oxford University Press. ISBN 978-0-19-881431-3. مؤرشف من الأصل في 12 أبريل 2020. الوسيط |CitationClass= تم تجاهله (مساعدة)

[:02-68] George Brinton; Weir, Maurice D.; Hass, Joel (2010). Thomas' Calculus (باللغة الإنجليزية). Pearson. ISBN 978-0-321-64363-6. مؤرشف من الأصل في 19 فبراير 2020. الوسيط |CitationClass= تم تجاهله (مساعدة)

[مولد_تلقائيا6-69] Richard A. (2014-04-15). Modern Calculus and Analytic Geometry (باللغة الإنجليزية). Courier Corporation. ISBN 978-0-486-79398-6. مؤرشف من الأصل في 25 فبراير 2020. الوسيط |CitationClass= تم تجاهله (مساعدة)

[70] Lindeburg, Michael R. (2012). Civil Engineering Reference Manual for the PE Exam. Professional Publications, Inc. صفحة 78-7. ISBN 978-1-59126-380-7. الوسيط |CitationClass= تم تجاهله (مساعدة)

[71] Benjamin (1861). Elements of Plane and Spherical Trigonometry: With Practical Applications (باللغة الإنجليزية). R. S. Davis. الوسيط |CitationClass= تم تجاهله (مساعدة)

[:2-73] Tim (2019-05-23). The Essential Calculus Workbook: Trigonometric Functions (باللغة الإنجليزية). Questing Vole Press. مؤرشف من الأصل في 28 فبراير 2020. الوسيط |CitationClass= تم تجاهله (مساعدة)

[74] Geoffrey C.; Rockett, Andrew M. (2015-01-01). Applied Calculus (باللغة الإنجليزية). Cengage Learning. ISBN 978-1-305-46505-3. مؤرشف من الأصل في 24 فبراير 2020. الوسيط |CitationClass= تم تجاهله (مساعدة)

[مولد_تلقائيا1-76] Protter & Morrey (1970, pp. APP-2,APP-3)

[Heng-78] Heng, Cheng and Talbert, "Additional Mathematics" نسخة محفوظة 2015-03-20 على موقع واي باك مشين., page 228

[:14-79] Coxford, Arthur (1987). Trigonometry. الوسيط |CitationClass= تم تجاهله (مساعدة)

[80] Bityutskov, V.I. (2011-02-07). "Trigonometric Functions". Encyclopedia of Mathematics (باللغة الإنجليزية). مؤرشف من الأصل في 29 ديسمبر 2017. اطلع عليه بتاريخ 29 ديسمبر 2017. الوسيط |CitationClass= تم تجاهله (مساعدة)

[85] Weisstein, Eric W. "Circular Functions". mathworld.wolfram.com (باللغة الإنجليزية). مؤرشف من الأصل في 3 أبريل 2017. اطلع عليه بتاريخ 01 مارس 2020. الوسيط |CitationClass= تم تجاهله (مساعدة)

[مولد_تلقائيا9-86] د فرانك; موير, د روبرت (2004-03-01). سلسلة ملخصات شوم ايزي ; حساب المثلثات. international house for cultural investments. ISBN 978-977-282-145-7. مؤرشف من الأصل في 25 فبراير 2020. الوسيط |CitationClass= تم تجاهله (مساعدة)

[Larson_2013-87] Larson, Ron (2013). Trigonometry (الطبعة 9th). Cengage Learning. صفحة 153. ISBN 978-1-285-60718-4. مؤرشف من الأصل في 15 فبراير 2018. الوسيط |CitationClass= تم تجاهله (مساعدة) Extract of page 153 نسخة محفوظة 2018-02-15 على موقع واي باك مشين.

[88] Schaumberger, Norman (1974-01-01). "A Classroom Theorem on Trigonometric Irrationalities". The Two-Year College Mathematics Journal. 5 (1): 73–76. doi:10.2307/3026991. مؤرشف من الأصل في 13 أكتوبر 2019. الوسيط |CitationClass= تم تجاهله (مساعدة)

[niven-89] Niven, Ivan (1956). Irrational Numbers. Mathematical Association of America. صفحة 41. MR = 0080123 0080123. مؤرشف من الأصل في 9 يونيو 2020. الوسيط |CitationClass= تم تجاهله (مساعدة)

[90] A proof for the cosine case appears as Lemma 12 in Bennett, Curtis D.; Glass, A. M. W.; Székely, Gábor J. (2004). "Fermat's last theorem for rational exponents". American Mathematical Monthly. 111 (4): 322–329. doi:10.2307/4145241. JSTOR 4145241. MR = 2057186 2057186. الوسيط |CitationClass= تم تجاهله (مساعدة)

[91] يتم الحصول على قيم دقيقة للدوال باستخدام متطابقات مجموع أو فرق زاويتين، على سبيل المثال: $cos(15°)=cos(60° - 45°)$

[:7-92] Weisstein, Eric W. "Trigonometry Angles--Pi/9". mathworld.wolfram.com (باللغة الإنجليزية). مؤرشف من الأصل في 30 ديسمبر 2019. اطلع عليه بتاريخ 04 أبريل 2020. الوسيط |CitationClass= تم تجاهله (مساعدة)

[93] M. Ram; Rath, Purusottam (2014-06-24). Transcendental Numbers (باللغة الإنجليزية). Springer. ISBN 978-1-4939-0832-5. مؤرشف من الأصل في 12 أبريل 2020. الوسيط |CitationClass= تم تجاهله (مساعدة)

[Abramowitz_and_Stegun-94] Abramowitz, Milton and Irene A. Stegun, p.74

[95] Milton; Stegun, Irene A. (1965-01-01). Handbook of Mathematical Functions: With Formulas, Graphs, and Mathematical Tables (باللغة الإنجليزية). Courier Corporation. ISBN 978-0-486-61272-0. مؤرشف من الأصل في 25 فبراير 2020. الوسيط |CitationClass= تم تجاهله (مساعدة)

[NASA-96] "«FORMULAS FOR nth ORDER DERIVATIVES OF HYPERBOLIC. AND TRIGONOMETRIC FUNCTIONS»" (PDF). NASA. مؤرشف من الأصل (PDF) في 12 مارس 2017. الوسيط |CitationClass= تم تجاهله (مساعدة)

[97] Timothy; Barrow-Green, June; Leader, Imre (2010-07-18). The Princeton Companion to Mathematics (باللغة الإنجليزية). Princeton University Press. ISBN 978-1-4008-3039-8. مؤرشف من الأصل في 19 فبراير 2020. الوسيط |CitationClass= تم تجاهله (مساعدة)

[98] Trigonometric functions. V.I. Bityutskov (originator), Encyclopedia of Mathematics. نسخة محفوظة 19 فبراير 2020 على موقع واي باك مشين.

[مولد_تلقائيا7-99] "Sine: Introduction to the trigonometric functions (subsection Trigonometrics/05)". functions.wolfram.com. مؤرشف من الأصل في 2 مايو 2016. اطلع عليه بتاريخ 14 أبريل 2020. الوسيط |CitationClass= تم تجاهله (مساعدة)

[:11-100] William E. Boyce, Richard C. DiPrima, Douglas B. Meade. Elementary Differential Equations and Boundary Value Problems (باللغة الإنجليزية). الوسيط |CitationClass= تم تجاهله (مساعدة)صيانة CS1: أسماء متعددة: قائمة المؤلفون (link)

[:83-101] Thomas & Finney 1996، §8.9

[102] Thomas & Finney 1996, §8.9. الوسيط |CitationClass= تم تجاهله (مساعدة)

[103] Ahlfors, pages 43–44.

[105] Michael T. (2007-06-18). Introduction to Mathematical Physics (باللغة الإنجليزية). John Wiley & Sons. ISBN 978-3-527-40627-2. مؤرشف من الأصل في 12 أبريل 2020. الوسيط |CitationClass= تم تجاهله (مساعدة)

[106] Abramowitz; Weisstein.

[107] Weisstein, Eric W. "Pole". mathworld.wolfram.com (باللغة الإنجليزية). مؤرشف من الأصل في 18 مارس 2020. اطلع عليه بتاريخ 09 أبريل 2020. الوسيط |CitationClass= تم تجاهله (مساعدة)

[108] Stanley, Enumerative Combinatorics, Vol I., page 149

[109] Green, Robin. "Faster Math Functions" (PDF). صفحة 6–7. مؤرشف من الأصل (PDF) في 23 مارس 2020. الوسيط |CitationClass= تم تجاهله (مساعدة)

[Aigner_2000-110] Aigner, Martin; Ziegler, Günter M. (2000). Proofs from THE BOOK (الطبعة Second). سبرنجر. صفحة 149. ISBN 978-3-642-00855-9. مؤرشف من الأصل في 08 مارس 2014. الوسيط |CitationClass= تم تجاهله (مساعدة)

[Remmert_1991-111] Remmert, Reinhold (1991). Theory of complex functions. Springer. صفحة 327. ISBN 978-0-387-97195-7. مؤرشف من الأصل في 20 مارس 2015. الوسيط |CitationClass= تم تجاهله (مساعدة) Extract of page 327 نسخة محفوظة 2015-03-20 على موقع واي باك مشين.

[112] Omar (2016-02-09). Introduction to Calculus and Classical Analysis (باللغة الإنجليزية). Springer. ISBN 978-3-319-28400-2. مؤرشف من الأصل في 12 أبريل 2020. الوسيط |CitationClass= تم تجاهله (مساعدة)

[:6-113] Luis Manuel Braga da Costa (2012-04-04). Transcendental Representations with Applications to Solids and Fluids (باللغة الإنجليزية). CRC Press. ISBN 978-1-4398-3431-2. مؤرشف من الأصل في 03 مارس 2020. الوسيط |CitationClass= تم تجاهله (مساعدة)

[Kannappan_2009-115] Kannappan, Palaniappan (2009). Functional Equations and Inequalities with Applications. Springer. ISBN 978-0387894911. الوسيط |CitationClass= تم تجاهله (مساعدة)

[116] John H.; Howell, Russell W. (2006). Complex Analysis for Mathematics and Engineering (باللغة الإنجليزية). Jones & Bartlett Learning. ISBN 978-0-7637-3748-1. مؤرشف من الأصل في 22 مارس 2016. الوسيط |CitationClass= تم تجاهله (مساعدة)

[117] Gandhi, Viswanathan (07-10-2014). "Domain coloring for visualizing complex functions". مؤرشف من الأصل في 12 أبريل 2020. الوسيط |CitationClass= تم تجاهله (مساعدة); تحقق من التاريخ في: |تاريخ= (مساعدة)

[119] The Princeton Companion to Mathematics. صفحة 307 - 308. الوسيط |CitationClass= تم تجاهله (مساعدة)

[120] Olver, NIST Handbook of Mathematical Functions. صفحة 122. الوسيط |CitationClass= تم تجاهله (مساعدة)

[122] Elementary Differential Equations and Boundary Value Problems. صفحة 376. الوسيط |CitationClass= تم تجاهله (مساعدة)

[124] David W. (2008-01-17). A First Course in Fourier Analysis (باللغة الإنجليزية). Cambridge University Press. ISBN 978-1-139-46903-6. مؤرشف من الأصل في 12 مارس 2020. الوسيط |CitationClass= تم تجاهله (مساعدة)

[125] Marcus (2010-01-07). Linear Partial Differential Equations and Fourier Theory (باللغة الإنجليزية). Cambridge University Press. ISBN 978-0-521-19970-4. مؤرشف من الأصل في 13 أبريل 2020. الوسيط |CitationClass= تم تجاهله (مساعدة)

[126] "More Approximations to Trigonometric Functions" (PDF). مؤرشف من الأصل (PDF) في 23 مارس 2020. الوسيط |CitationClass= تم تجاهله (مساعدة)

[127] Kantabutra, Vitit (1996). "On hardware for computing exponential and trigonometric functions" – عبر IEEE Transactions on Computers. الوسيط |CitationClass= تم تجاهله (مساعدة)

[128] Jurgen; Platzner, Marco (2004-08-19). Field Programmable Logic and Application: 14th International Conference , FPL 2004, Leuven, Belgium, August 30-September 1, 2004, Proceedings (باللغة الإنجليزية). Springer Science & Business Media. ISBN 978-3-540-22989-6. مؤرشف من الأصل في 12 أبريل 2020. الوسيط |CitationClass= تم تجاهله (مساعدة)

[129] "التنفیذ المادي باستخدام FPGA لخوارزمیتي كوردك وجدول المقارنة لحساب الدوال الریاضیة الأولیة". المجلات الأكاديمية العلمية العراقية. مؤرشف من الأصل في 12 أبريل 2020. الوسيط |CitationClass= تم تجاهله (مساعدة)

[130] P, BrentRichard (1976-04-01). "Fast Multiple-Precision Evaluation of Elementary Functions". Journal of the ACM (JACM) (باللغة الإنجليزية). doi:10.1145/321941.321944. مؤرشف من الأصل في 12 أبريل 2020. الوسيط |CitationClass= تم تجاهله (مساعدة)

[131] "Weierstrass Substitution". Math24 (باللغة الإنجليزية). مؤرشف من الأصل في 27 مارس 2020. اطلع عليه بتاريخ 27 مارس 2020. الوسيط |CitationClass= تم تجاهله (مساعدة)

[132] Selby 1970، pg. 190

[133] Abramowitz and Stegun. Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables. صفحة 72. الوسيط |CitationClass= تم تجاهله (مساعدة)

[135] غياث الدين الكاشي. مفتاح الحساب. الوسيط |CitationClass= تم تجاهله (مساعدة)

[136] Clifford A. (2009). The Math Book: From Pythagoras to the 57th Dimension, 250 Milestones in the History of Mathematics (باللغة الإنجليزية). Sterling Publishing Company, Inc. ISBN 978-1-4027-5796-9. مؤرشف من الأصل في 30 مارس 2017. الوسيط |CitationClass= تم تجاهله (مساعدة)

[Ireneus-137] Romuald Ireneus 'Scibor-Marchocki, Spherical trigonometry, Elementary-Geometry Trigonometry web page (1997). نسخة محفوظة 21 أبريل 2020 على موقع واي باك مشين.

[VNR-138] W. Gellert, S. Gottwald, M. Hellwich, H. Kästner, and H. Küstner, The VNR Concise Encyclopedia of Mathematics, 2nd ed., ch. 12 (Van Nostrand Reinhold: New York, 1989).

[139] Todhunter, I. (1886). Spherical Trigonometry (الطبعة 5th). MacMillan. مؤرشف من الأصل في 14 أبريل 2020. الوسيط |CitationClass= تم تجاهله (مساعدة)

[Allen_1976-140] The Universal Encyclopaedia of Mathematics, Pan Reference Books, 1976, page 529-530. English version George Allen and Unwin, 1964. Translated from the German version Meyers Rechenduden, 1960.

[مولد_تلقائيا4-141] Daniel Zwillinger, CRC Standard Mathematical Tables and Formulae, 32nd Edition, CRC Press, 2011, page 219.

[142] Modern calculus with analytic geometry, Volume 1. صفحة 105-106. الوسيط |CitationClass= تم تجاهله (مساعدة)

[143] Calculus and Analytic Geometry. صفحة 138. الوسيط |CitationClass= تم تجاهله (مساعدة)

[144] Olver, NIST Handbook of Mathematical Functions. صفحة 116. الوسيط |CitationClass= تم تجاهله (مساعدة)

[145] Ernest William (1891). A Treatise on Plane Trigonometry (باللغة الإنجليزية). University Press. مؤرشف من الأصل في 12 أبريل 2020. الوسيط |CitationClass= تم تجاهله (مساعدة)

[146] Michael Sullivan, Trigonometry, Dellen Publishing Company, 1988, page 243.

[147] W. A. Beyer, J. D. Louck, and D. Zeilberger, A Generalization of a Curiosity that Feynman Remembered All His Life, Math. Mag. 69, 43–44, 1996.

[:03-148] Arthur Graham; Frink, Fred Goodrich ([c1909]). Plane trigonometry. New York : Henry Holt. مؤرشف من الأصل في 13 أبريل 2020. الوسيط |CitationClass= تم تجاهله (مساعدة); تحقق من التاريخ في: |تاريخ= (مساعدة)

[149] Weisstein, Eric W. "Inverse Trigonometric Functions". mathworld.wolfram.com (باللغة الإنجليزية). مؤرشف من الأصل في 13 أبريل 2020. اطلع عليه بتاريخ 13 أبريل 2020. الوسيط |CitationClass= تم تجاهله (مساعدة)

[:12-150] V. G.; Argunov, B. I.; Skornyakov, L. A.; Boltyanskii, V. G. (2013-11-07). Hyperbolic Functions: with Configuration Theorems and Equivalent and Equidecomposable Figures (باللغة الإنجليزية). Courier Corporation. ISBN 978-0-486-17005-3. مؤرشف من الأصل في 12 أبريل 2020. الوسيط |CitationClass= تم تجاهله (مساعدة)

[:13-151] "Hyperbolic functions" (PDF). Mathcentre. 9 يناير 2006. مؤرشف من الأصل (PDF) في 9 سبتمبر 2019. الوسيط |CitationClass= تم تجاهله (مساعدة)

[153] Árpád (2010-05-25). Generalized Bessel Functions of the First Kind (باللغة الإنجليزية). Springer Science & Business Media. ISBN 978-3-642-12229-3. مؤرشف من الأصل في 14 مارس 2020. الوسيط |CitationClass= تم تجاهله (مساعدة)

[154] United States National Bureau of (1952). Tables of Chebyshev Polynomials (باللغة الإنجليزية). U.S. Government Printing Office. مؤرشف من الأصل في 14 مارس 2020. الوسيط |CitationClass= تم تجاهله (مساعدة)

[157] Robert; Halliday, David; Krane, Kenneth S. (1992-03-16). Physics (باللغة الإنجليزية). Wiley. ISBN 978-0-471-80457-4. مؤرشف من الأصل في 19 فبراير 2020. الوسيط |CitationClass= تم تجاهله (مساعدة)

[مولد_تلقائيا15-159] "Area Formulas". www.math.com. مؤرشف من الأصل في 15 مايو 2020. اطلع عليه بتاريخ 21 مايو 2020. الوسيط |CitationClass= تم تجاهله (مساعدة)

[160] "Area of Triangle Using Trigonometry - MathBitsNotebook(Geo - CCSS Math)". mathbitsnotebook.com. مؤرشف من الأصل في 29 أكتوبر 2019. اطلع عليه بتاريخ 21 مايو 2020. الوسيط |CitationClass= تم تجاهله (مساعدة)

[مولد_تلقائيا13-161] Aaron (1875). Plane and Spherical Trigonometry and Mensuration (باللغة الإنجليزية). American Book Company. مؤرشف من الأصل في 22 مايو 2020. الوسيط |CitationClass= تم تجاهله (مساعدة)

[مولد_تلقائيا14-163] Max; Association, Research and Education (1984-01-01). Handbook of Mathematical, Scientific, and Engineering Formulas, Tables, Functions, Graphs, Transforms (باللغة الإنجليزية). Research & Education Assoc. ISBN 978-0-87891-521-7. مؤرشف من الأصل في 22 مايو 2020. الوسيط |CitationClass= تم تجاهله (مساعدة)

[164] Ron; Edwards, Bruce H. (2010-01-01). Calculus of a Single Variable: Early Transcendental Functions (باللغة الإنجليزية). Cengage Learning. ISBN 978-0-538-73552-0. مؤرشف من الأصل في 22 مايو 2020. الوسيط |CitationClass= تم تجاهله (مساعدة)

[165] Isaac (1878). Spherical Trigonometry, for the Use of Colleges and Schools: With Numerous Examples (باللغة الإنجليزية). Macmillan. الوسيط |CitationClass= تم تجاهله (مساعدة)

[166] Gilbert (1991-01-01). Calculus (باللغة الإنجليزية). SIAM. ISBN 978-0-9614088-2-4. مؤرشف من الأصل في 12 أبريل 2020. الوسيط |CitationClass= تم تجاهله (مساعدة)

[167] Milton; Stegun, Irene A. (2012-04-30). Handbook of Mathematical Functions: with Formulas, Graphs, and Mathematical Tables (باللغة الإنجليزية). Courier Corporation. ISBN 978-0-486-15824-2. مؤرشف من الأصل في 19 فبراير 2020. الوسيط |CitationClass= تم تجاهله (مساعدة)

[168] An Elementary Treatise on Plane and Spherical Trigonometry with their applications to navigation, surveying heights and distances, and spherical astronomy; and particularly adapted to explaining the construction of Bowditch's Navigator ... Third edition, with additions (باللغة الإنجليزية). 1845. مؤرشف من الأصل في 12 أبريل 2020. الوسيط |CitationClass= تم تجاهله (مساعدة)

[169] Michael; Backman, Dana (2009-01-05). Astronomy: The Solar System and Beyond (باللغة الإنجليزية). Cengage Learning. ISBN 978-0-495-56203-0. مؤرشف من الأصل في 12 أبريل 2020. الوسيط |CitationClass= تم تجاهله (مساعدة)

[171] عاصی، محمدرضا. نقشه‌برداری (ژئوماتیک) (ویراست چهارم) (باللغة الفارسية). انتشارات علمی دانشگاه ضنعتی شریف. ISBN 978-964-208-008-3. الوسيط |CitationClass= تم تجاهله (مساعدة)

[172] "Solving ASA Triangles". www.mathsisfun.com. مؤرشف من الأصل في 01 يوليو 2018. اطلع عليه بتاريخ 28 مايو 2020. الوسيط |CitationClass= تم تجاهله (مساعدة)

[173] Геометрия. 7-9 классы. Учебник. ФГОС, размер 165x220 мм. Атанасян Левон Сергеевич (باللغة الروسية). ISBN 978-5-09-021136-9. الوسيط |CitationClass= تم تجاهله (مساعدة)

[مولد_تلقائيا8-174] N. K. (2014-05-12). A Treatise on Trigonometric Series: Volume 1 (باللغة الإنجليزية). Elsevier. ISBN 978-1-4832-2419-0. مؤرشف من الأصل في 12 أبريل 2020. الوسيط |CitationClass= تم تجاهله (مساعدة)

[175] Weisstein, Eric W. "Fourier Transform". mathworld.wolfram.com (باللغة الإنجليزية). مؤرشف من الأصل في 18 مارس 2020. اطلع عليه بتاريخ 14 أبريل 2020. الوسيط |CitationClass= تم تجاهله (مساعدة)

[176] Gerald B Folland. Fourier Analysis and its Applications. صفحات 225–234. الوسيط |CitationClass= تم تجاهله (مساعدة)

[177] "JPEG (Transform Compression)". www.dspguide.com. مؤرشف من الأصل في 20 يناير 2020. اطلع عليه بتاريخ 11 أبريل 2020. الوسيط |CitationClass= تم تجاهله (مساعدة)

[178] James R. (2010-11-08). Differential Equations with Boundary Value Problems: An Introduction to Modern Methods & Applications (باللغة الإنجليزية). John Wiley & Sons. ISBN 978-0-470-59535-0. مؤرشف من الأصل في 03 مارس 2020. الوسيط |CitationClass= تم تجاهله (مساعدة)

[179] Morris; Pollard, Harry (1985-10-01). Ordinary Differential Equations: An Elementary Textbook for Students of Mathematics, Engineering, and the Sciences (باللغة الإنجليزية). Courier Corporation. ISBN 978-0-486-64940-5. مؤرشف من الأصل في 03 مارس 2020. الوسيط |CitationClass= تم تجاهله (مساعدة)

[Farlow_1993-180] Farlow, Stanley J. (1993). Partial differential equations for scientists and engineers (الطبعة Reprint of Wiley 1982). Courier Dover Publications. صفحة 82. ISBN 978-0-486-67620-3. مؤرشف من الأصل في 20 مارس 2015. الوسيط |CitationClass= تم تجاهله (مساعدة)

[181] Gerald B Folland. Fourier Analysis and its Applications. صفحة 77ff. الوسيط |CitationClass= تم تجاهله (مساعدة)

[182] Peter J. (2013-11-08). Introduction to Partial Differential Equations (باللغة الإنجليزية). Springer Science & Business Media. ISBN 978-3-319-02099-0. مؤرشف من الأصل في 12 أبريل 2020. الوسيط |CitationClass= تم تجاهله (مساعدة)

[183] Lawrence (2013-09-25). Advanced Engineering Mathematics (باللغة الإنجليزية). CRC Press. ISBN 978-1-4398-3447-3. مؤرشف من الأصل في 12 أبريل 2020. الوسيط |CitationClass= تم تجاهله (مساعدة)

[184] "Parametric Equation of a Circle - Math Open Reference". www.mathopenref.com. مؤرشف من الأصل في 18 نوفمبر 2019. اطلع عليه بتاريخ 25 مايو 2020. الوسيط |CitationClass= تم تجاهله (مساعدة)

[:91-185] "Welcome to CK-12 Foundation | CK-12 Foundation". www.ck12.org. مؤرشف من الأصل في 17 فبراير 2017. اطلع عليه بتاريخ 25 مايو 2020. الوسيط |CitationClass= تم تجاهله (مساعدة)

[186] Weisstein, Eric W. "Lissajous Curve". mathworld.wolfram.com (باللغة الإنجليزية). مؤرشف من الأصل في 15 نوفمبر 2019. اطلع عليه بتاريخ 25 مايو 2020. الوسيط |CitationClass= تم تجاهله (مساعدة)

[187] Francis A.; White, Harvey E. (1937). Fundamentals of Optics (باللغة الإنجليزية). Tata McGraw-Hill Education. ISBN 978-1-259-00229-8. مؤرشف من الأصل في 24 فبراير 2020. الوسيط |CitationClass= تم تجاهله (مساعدة)

[189] Vasiliĭ Petrovich (1963). Navigation Instruments (باللغة الإنجليزية). Foreign Technology Division. مؤرشف من الأصل في 24 فبراير 2020. الوسيط |CitationClass= تم تجاهله (مساعدة)

[190] Halliday, Resnick and Krane ,Physics

[191] "Parametric Equations and Projectile Motion" (PDF). Classzone. مؤرشف من الأصل (PDF) في 12 أبريل 2020. الوسيط |CitationClass= تم تجاهله (مساعدة); line feed character في |عنوان= على وضع 25 (مساعدة)

[192] "Contemporary Physics". مؤرشف من الأصل في 22 أبريل 2020. الوسيط |CitationClass= تم تجاهله (مساعدة)

[FOOTNOTEKing198683-193] King 1986، صفحة 83.

[194] الصيغة التي تكافئها موجودة في Hadi Bashori 2015، صفحة 119

[FOOTNOTEHadi_Bashori2015119-195] Hadi Bashori 2015، صفحة 119.

[Electricity-197] Mark (2009-12-03). Professional English in Use Engineering with Answers: Technical English for Professionals (باللغة الإنجليزية). Cambridge University Press. ISBN 978-0-521-73488-2. مؤرشف من الأصل في 12 مارس 2020. الوسيط |CitationClass= تم تجاهله (مساعدة)

[:10-198] بررسی سیستم‌های قدرت (باللغة الفارسية). طهران. ISBN 964-454-394-7. الوسيط |CitationClass= تم تجاهله (مساعدة)

[200] "Electrical Power in AC Circuits and Reactive Power". مؤرشف من الأصل في 12 يوليو 2019. الوسيط |CitationClass= تم تجاهله (مساعدة)

[201] Alan V.; Willsky, Alan S.; Nawab, Syed Hamid (1997). Signals & Systems (باللغة الإنجليزية). Prentice-Hall International. ISBN 978-0-13-651175-5. مؤرشف من الأصل في 12 أبريل 2020. الوسيط |CitationClass= تم تجاهله (مساعدة)