تفاضل الدوال المثلثية

دائرة ذات المركز O ونصف القطر 1

العصر: منحنيا y = 1 و y = cos θ موضحة باللون الأحمر، ومنحنى y = sin(θ)/θ موضح باللون الأزرق.

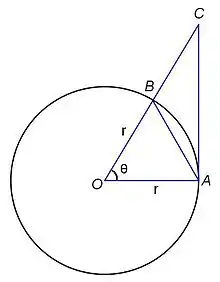
يوضح الرسم البياني الموجود على اليسار دائرة ذات المركز O ونصف القطر r = 1. لتكن OA و OB اثنين من نصف القطر يصنعان قوس قياسه θ راديان. بما أننا اعتبرنا النهاية لما θ يؤول إلى الصفر، فقد نفترض أن θ هو عدد موجب صغير، نقول 0 < θ < ½ في الربع الأول.

في الرسم البياني، ليكن R₁ المثلث OAB و R₂ القطاع الدائري OAB و R₃ المثلث OAC. مساحة المثلث OAB هي:

${\displaystyle \mathrm {Area} (R_{1})={\tfrac {1}{2}}\ |OA|\ |OB|\sin \theta ={\tfrac {1}{2}}\sin \theta \,.}$

مساحة القطاع الدائري OAB هي: ${\displaystyle \mathrm {Area} (R_{2})={\tfrac {1}{2}}\theta }$، بينما مساحة المثلث OAC معطاة بواسطة:

${\displaystyle \mathrm {Area} (R_{3})={\tfrac {1}{2}}\ |OA|\ |AC|={\tfrac {1}{2}}\tan \theta \,.}$

بما أن كل منطقة تقع في المنطقة التالية، فإن:

${\displaystyle {\text{Area}}(R_{1})<{\text{Area}}(R_{2})<{\text{Area}}(R_{3})\iff {\tfrac {1}{2}}\sin \theta <{\tfrac {1}{2}}\theta <{\tfrac {1}{2}}\tan \theta \,.}$

زيادة على ذلك، بما أن sin θ > 0 في الربع الأول، فيمكننا القسمة على ½ sin θ، معطيًا:

${\displaystyle 1<{\frac {\theta }{\sin \theta }}<{\frac {1}{\cos \theta }}\implies 1>{\frac {\sin \theta }{\theta }}>\cos \theta \,.}$

في الخطوة الأخيرة، أخذنا مقاليب الحدود الموجبة الثلاثة، وعكسنا المتباينة.

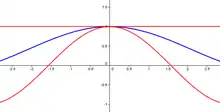
نستنتج أنه من أجل 0 < θ < ½ π، يكون مقدار sin(θ)/θ دائما أقل من 1 ودائمًا أكبر من cos(θ). وهكذا، عندما تقترب θ من 0، فإن sin(θ)/θ "عُصِرت" بين سقف ارتفاعه 1 وأرضية ارتفاعها cos θ، والتي ترتفع نحو 1؛ لذلك يجب أن تؤول sin(θ)/θ إلى 1؛ حيث أن θ تؤول إلى 0 من الجهة الموجبة:

${\displaystyle \lim _{\theta \to 0^{+}}{\frac {\sin \theta }{\theta }}=1\,.}$

بالنسبة للحالة التي تكون فيها θ عددًا سالبًا صغيرًا –½ π < θ < 0، نستخدم حقيقة أن الجيب دالة فردية:

${\displaystyle \lim _{\theta \to 0^{-}}\!{\frac {\sin \theta }{\theta }}\ =\ \lim _{\theta \to 0^{+}}\!{\frac {\sin(-\theta )}{-\theta }}\ =\ \lim _{\theta \to 0^{+}}\!{\frac {-\sin \theta }{-\theta }}\ =\ \lim _{\theta \to 0^{+}}\!{\frac {\sin \theta }{\theta }}\ =\ 1\,.}$

يتيح لنا القسم الأخير حساب هذه النهاية الجديدة بسهولة نسبية. يتم ذلك عن طريق استخدام خدعة بسيطة. في هذا الحساب، إشارة θ غير مهمة.

${\displaystyle \lim _{\theta \to 0}\,{\frac {\cos \theta -1}{\theta }}\ =\ \lim _{\theta \to 0}\left({\frac {\cos \theta -1}{\theta }}\right)\!\!\left({\frac {\cos \theta +1}{\cos \theta +1}}\right)\ =\ \lim _{\theta \to 0}\,{\frac {\cos ^{2}\!\theta -1}{\theta \,(\cos \theta +1)}}.}$

باستخدام هذه المتطابقة cos²θ – 1 = –sin²θ، حقيقة أن نهاية الجداء هو جداء النهايات، ونتيجة النهاية من القسم السابق، نجد أن:

${\displaystyle \lim _{\theta \to 0}\,{\frac {\cos \theta -1}{\theta }}\ =\ \lim _{\theta \to 0}\,{\frac {-\sin ^{2}\theta }{\theta (\cos \theta +1)}}\ =\ \left(-\lim _{\theta \to 0}{\frac {\sin \theta }{\theta }}\right)\!\left(\lim _{\theta \to 0}\,{\frac {\sin \theta }{\cos \theta +1}}\right)\ =\ (-1)\left({\frac {0}{2}}\right)=0\,.}$

باستخدام نهاية دالة الجيب، وحقيقة أن دالة الظل فردية، وحقيقة أن نهاية الجداء هو جداء النهايات، نجد:

${\displaystyle \lim _{\theta \to 0}{\frac {\tan \theta }{\theta }}\ =\ \left(\lim _{\theta \to 0}{\frac {\sin \theta }{\theta }}\right)\!\left(\lim _{\theta \to 0}{\frac {1}{\cos \theta }}\right)\ =\ (1)(1)\ =\ 1\,.}$

نحسب مشتق دالة الجيب باستخدام تعريف بواسطة النهاية:

${\displaystyle {\frac {\operatorname {d} }{\operatorname {d} \!\theta }}\,\sin \theta =\lim _{\delta \to 0}{\frac {\sin(\theta +\delta )-\sin \theta }{\delta }}.}$

باستخدام متطابقة مجموع زاويتين sin(α+β) = sin α cos β + sin β cos α، لدينا:

${\displaystyle {\frac {\operatorname {d} }{\operatorname {d} \!\theta }}\,\sin \theta =\lim _{\delta \to 0}{\frac {\sin \theta \cos \delta +\sin \delta \cos \theta -\sin \theta }{\delta }}=\lim _{\delta \to 0}\left({\frac {\sin \delta }{\delta }}\cos \theta +{\frac {\cos \delta -1}{\delta }}\sin \theta \right).}$

باستخدام نهايتي كل من دالة الجيب وجيب التمام:

${\displaystyle {\frac {\operatorname {d} }{\operatorname {d} \!\theta }}\,\sin \theta =(1)\cos \theta +(0)\sin \theta =\cos \theta \,.}$

مرة أخرى نحسب مشتق دالة جيب التمام من تعريف بواسطة النهاية:

باستخدام متطابقة مجموع زاويتين cos(α+β) = cos α cos β – sin α sin β، لدينا:

${\displaystyle {\frac {\operatorname {d} }{\operatorname {d} \!\theta }}\,\cos \theta =\lim _{\delta \to 0}{\frac {\cos \theta \cos \delta -\sin \theta \sin \delta -\cos \theta }{\delta }}=\lim _{\delta \to 0}\left({\frac {\cos \delta -1}{\delta }}\cos \theta \,-\,{\frac {\sin \delta }{\delta }}\sin \theta \right).}$

باستخدام النهايات الأولى:

${\displaystyle {\frac {\operatorname {d} }{\operatorname {d} \!\theta }}\,\cos \theta =(0)\cos \theta -(1)\sin \theta =-\sin \theta \,.}$

لحساب مشتق دالة جيب التمام من قاعدة السلسلة[ملاحظة 1]، لاحظ أولاً الحقائق الثلاث التالية:

${\displaystyle \cos \theta =\sin \left({\tfrac {\pi }{2}}-\theta \right)}$

${\displaystyle \sin \theta =\cos \left({\tfrac {\pi }{2}}-\theta \right)}$

${\displaystyle {\tfrac {\operatorname {d} }{\operatorname {d} \!\theta }}\sin \theta =\cos \theta }$

الأولى والثانية هما متطبقتان مثلثيتان، والثالث تم إثباته أعلاه. باستخدام هذه الحقائق الثلاث، يمكننا كتابة ما يلي:

${\displaystyle {\tfrac {\operatorname {d} }{\operatorname {d} \!\theta }}\cos \theta ={\tfrac {\operatorname {d} }{\operatorname {d} \!\theta }}\sin \left({\tfrac {\pi }{2}}-\theta \right)}$

يمكن اشتقاقها باستخدام قاعدة السلسلة. لتكن ${\displaystyle f(x)=\sin x}$ و ${\displaystyle g(\theta )={\tfrac {\pi }{2}}-\theta }$، لدينا:

${\displaystyle {\tfrac {\operatorname {d} }{\operatorname {d} \!\theta }}f\!\left(g\!\left(\theta \right)\right)=f^{\prime }\!\left(g\!\left(\theta \right)\right)\cdot g^{\prime }\!\left(\theta \right)=\cos \left({\tfrac {\pi }{2}}-\theta \right)\cdot (0-1)=-\sin \theta }$

إذن:

${\displaystyle {\tfrac {\operatorname {d} }{\operatorname {d} \!\theta }}\cos \theta =-\sin \theta }$.

لحساب مشتق دالة الظل tan θ، نستخدم تعريف بواسطة النهاية:

${\displaystyle {\frac {\operatorname {d} }{\operatorname {d} \!\theta }}\,\tan \theta =\lim _{\delta \to 0}\left({\frac {\tan(\theta +\delta )-\tan \theta }{\delta }}\right).}$

باستخدام المتطابقة المعروفة: tan(α+β) = (tan α + tan β) / (1 - tan α tan β)، لدينا:

${\displaystyle {\frac {\operatorname {d} }{\operatorname {d} \!\theta }}\,\tan \theta =\lim _{\delta \to 0}\left[{\frac {{\frac {\tan \theta +\tan \delta }{1-\tan \theta \tan \delta }}-\tan \theta }{\delta }}\right]=\lim _{\delta \to 0}\left[{\frac {\tan \theta +\tan \delta -\tan \theta +\tan ^{2}\theta \tan \delta }{\delta \left(1-\tan \theta \tan \delta \right)}}\right].}$

باستخدام حقيقة أن نهاية الجداء هو جداء نهايتين:

${\displaystyle {\frac {\operatorname {d} }{\operatorname {d} \!\theta }}\,\tan \theta =\lim _{\delta \to 0}{\frac {\tan \delta }{\delta }}\times \lim _{\delta \to 0}\left({\frac {1+\tan ^{2}\theta }{1-\tan \theta \tan \delta }}\right).}$

باستخدام النهاية الخاصة بدالة الظل، وحقيقة أن tan δ يؤول إلى 0 حيث δ يؤول إلى 0:

${\displaystyle {\frac {\operatorname {d} }{\operatorname {d} \!\theta }}\,\tan \theta =1\times {\frac {1+\tan ^{2}\theta }{1-0}}=1+\tan ^{2}\theta .}$

نرى على الفور أن:

${\displaystyle {\frac {\operatorname {d} }{\operatorname {d} \!\theta }}\,\tan \theta =1+{\frac {\sin ^{2}\theta }{\cos ^{2}\theta }}={\frac {\cos ^{2}\theta +\sin ^{2}\theta }{\cos ^{2}\theta }}={\frac {1}{\cos ^{2}\theta }}=\sec ^{2}\theta \,.}$

يمكن للمرء حساب مشتق دالة الظل باستخدام قاعدة ناتج القسمة.

${\displaystyle {\frac {\operatorname {d} }{\operatorname {d} \!\theta }}\tan \theta ={\frac {\operatorname {d} }{\operatorname {d} \!\theta }}{\frac {\sin \theta }{\cos \theta }}={\frac {\left(\sin \theta \right)^{\prime }\cdot \cos \theta -\sin \theta \cdot \left(\cos \theta \right)^{\prime }}{\cos ^{2}\theta }}={\frac {\cos ^{2}\theta +\sin ^{2}\theta }{\cos ^{2}\theta }}}$

يمكن تبسيط البسط إلى 1 بواسطة متطابقة فيثاغورس، يعطينا:

${\displaystyle {\frac {1}{\cos ^{2}\theta }}=\sec ^{2}\theta }$

إذن:

${\displaystyle {\frac {\operatorname {d} }{\operatorname {d} \!\theta }}\tan \theta =\sec ^{2}\theta }$

نعتبر الدالة

${\displaystyle y=\arcsin x\,\!}$

حيث

${\displaystyle -{\frac {\pi }{2}}\leq y\leq {\frac {\pi }{2}}}$

بالتعريف

${\displaystyle \sin y=x\,\!}$

نشتق كلا طرفي الأخيرة بالنسبة لـ ${\displaystyle x}$ وحل لـ dy/dx:

${\displaystyle {d \over dx}\sin y={d \over dx}x}$

${\displaystyle \cos y\cdot {dy \over dx}=1\,\!}$

نعوض بـ ${\displaystyle \cos y={\sqrt {1-\sin ^{2}y}}}$:

${\displaystyle {\sqrt {1-\sin ^{2}y}}\cdot {dy \over dx}=1}$

نعوض بـ ${\displaystyle x=\sin y}$:

${\displaystyle {\sqrt {1-x^{2}}}\cdot {dy \over dx}=1}$

${\displaystyle {dy \over dx}={\frac {1}{\sqrt {1-x^{2}}}}}$

نعتبر الدالة

${\displaystyle y=\arccos x\,\!}$

حيث

${\displaystyle 0\leq y\leq \pi }$

بالتعريف

${\displaystyle \cos y=x\,\!}$

نشتق كلا طرفي الأخيرة بالنسبة لـ ${\displaystyle x}$ وحل لـ dy/dx:

${\displaystyle {d \over dx}\cos y={d \over dx}x}$

${\displaystyle -\sin y\cdot {dy \over dx}=1}$

نعوض بـ ${\displaystyle \sin y={\sqrt {1-\cos ^{2}y}}\,\!}$:

${\displaystyle -{\sqrt {1-\cos ^{2}y}}\cdot {dy \over dx}=1}$

نعوض بـ ${\displaystyle x=\cos y\,\!}$:

${\displaystyle -{\sqrt {1-x^{2}}}\cdot {dy \over dx}=1}$

${\displaystyle {dy \over dx}=-{\frac {1}{\sqrt {1-x^{2}}}}}$

نعتبر الدالة

${\displaystyle y=\arctan x\,\!}$

حيث

${\displaystyle -{\frac {\pi }{2}}<y<{\frac {\pi }{2}}}$

بالتعريف

${\displaystyle \tan y=x\,\!}$

نشتق كلا طرفي الأخيرة بالنسبة لـ ${\displaystyle x}$ وحل لـ dy/dx:

${\displaystyle {d \over dx}\tan y={d \over dx}x}$

الطرف الأيسر:

${\displaystyle {d \over dx}\tan y=\sec ^{2}y\cdot {dy \over dx}=(1+\tan ^{2}y){dy \over dx}}$ باستخدام متطابقة فيثاغورس

الطرف الأيمن:

${\displaystyle {d \over dx}x=1}$

ومنه:

${\displaystyle (1+\tan ^{2}y){dy \over dx}=1}$

نعوض بـ ${\displaystyle x=\tan y\,\!}$ ، نحصل على:

${\displaystyle (1+x^{2}){dy \over dx}=1}$

${\displaystyle {dy \over dx}={\frac {1}{1+x^{2}}}}$

نعتبر الدالة

${\displaystyle y=\operatorname {arccot} x}$

حيث ${\displaystyle 0<y<\pi }$.

بالتعريف

${\displaystyle \cot y=x}$

نشتق كلا طرفي الأخيرة بالنسبة لـ ${\displaystyle x}$ وحل لـ dy/dx:

${\displaystyle {\frac {d}{dx}}\cot y={\frac {d}{dx}}x}$

الطرف الأيسر:

${\displaystyle {d \over dx}\cot y=-\csc ^{2}y\cdot {dy \over dx}=-(1+\cot ^{2}y){dy \over dx}}$ باستخدام متطابقة فيثاغورس

الطرف الأيمن:

${\displaystyle {d \over dx}x=1}$

ومنه،

${\displaystyle -(1+\cot ^{2}y){\frac {dy}{dx}}=1}$

نعوض بـ ${\displaystyle x=\cot y}$:

${\displaystyle -(1+x^{2}){\frac {dy}{dx}}=1}$

${\displaystyle {\frac {dy}{dx}}=-{\frac {1}{1+x^{2}}}}$

نعتبر الدالة:

${\displaystyle y=\operatorname {arcsec} x\ \ |x|\geq 1}$

بالتعريف

${\displaystyle x=\sec y\ \ y\in \left[0,{\frac {\pi }{2}}\right)\cup \left({\frac {\pi }{2}},\pi \right]}$

${\displaystyle {\frac {dx}{dy}}=\sec y\tan y=|x|{\sqrt {x^{2}-1}}}$

(القيمة المطلقة في التعبير ضرورية حيث أن جداء القاطع والظل في مجال y يكون دائمًا غير سالب، بينما العبارة ${\displaystyle {\sqrt {x^{2}-1}}}$ دائمًا غير سالبة بتعريف الجذر التربيعي الرئيسي، لذلك يجب أن يكون العامل المتبقي غير سالب، والذي يتحقق باستخدام القيمة المطلقة لـ x.)

${\displaystyle {\frac {dy}{dx}}={\frac {1}{|x|{\sqrt {x^{2}-1}}}}}$

بدلاً من ذلك، يمكن اشتقاق دالة القاطع العكسية من مشتق دالة جيب التمام العكسية باستخدام قاعدة السلسلة.

لتكن

${\displaystyle y=\operatorname {arcsec} x=\arccos \left({\frac {1}{x}}\right)}$

حيث

${\displaystyle |x|\geq 1}$ و ${\displaystyle y\in \left[0,{\frac {\pi }{2}}\right)\cup \left({\frac {\pi }{2}},\pi \right]}$

وبعد ذلك، بتطبيق قاعدة السلسلة على ${\displaystyle \arccos \left({\frac {1}{x}}\right)}$:

${\displaystyle {\frac {dy}{dx}}=-{\frac {1}{\sqrt {1-({\frac {1}{x}})^{2}}}}\cdot \left(-{\frac {1}{x^{2}}}\right)={\frac {1}{x^{2}{\sqrt {1-{\frac {1}{x^{2}}}}}}}={\frac {1}{x^{2}{\frac {\sqrt {x^{2}-1}}{\sqrt {x^{2}}}}}}={\frac {1}{{\sqrt {x^{2}}}{\sqrt {x^{2}-1}}}}={\frac {1}{|x|{\sqrt {x^{2}-1}}}}}$

لتكن

${\displaystyle y=\operatorname {arccsc} x\ \ |x|\geq 1}$

بالتعريف:

${\displaystyle x=\csc y\ \ \ y\in \left[-{\frac {\pi }{2}},0\right)\cup \left(0,{\frac {\pi }{2}}\right]}$

${\displaystyle {\frac {dx}{dy}}=-\csc y\cot y=-|x|{\sqrt {x^{2}-1}}}$

(القيمة المطلقة في التعبير ضرورية حيث أن جداء قاطع التمام وظل التمام في مجال y يكون دائمًا غير سالب، بينما العبارة ${\displaystyle {\sqrt {x^{2}-1}}}$ دائمًا غير سالبة بتعريف الجذر التربيعي الرئيسي، لذلك يجب أن يكون العامل المتبقي غير سالب، والذي يتحقق باستخدام القيمة المطلقة لـ x.)

${\displaystyle {\frac {dy}{dx}}={\frac {-1}{|x|{\sqrt {x^{2}-1}}}}}$

بدلاً من ذلك، يمكن اشتقاق دالة قاطع التمام العكسية من مشتق دالة الجيب العكسية باستخدام قاعدة السلسلة.

لتكن

${\displaystyle y=\operatorname {arccsc} x=\arcsin \left({\frac {1}{x}}\right)}$

حيث

${\displaystyle |x|\geq 1}$ و ${\displaystyle y\in \left[-{\frac {\pi }{2}},0\right)\cup \left(0,{\frac {\pi }{2}}\right]}$

وبعد ذلك، بتطبيق قاعدة السلسلة على ${\displaystyle \arcsin \left({\frac {1}{x}}\right)}$:

${\displaystyle {\frac {dy}{dx}}={\frac {1}{\sqrt {1-({\frac {1}{x}})^{2}}}}\cdot \left(-{\frac {1}{x^{2}}}\right)=-{\frac {1}{x^{2}{\sqrt {1-{\frac {1}{x^{2}}}}}}}=-{\frac {1}{x^{2}{\frac {\sqrt {x^{2}-1}}{\sqrt {x^{2}}}}}}=-{\frac {1}{{\sqrt {x^{2}}}{\sqrt {x^{2}-1}}}}=-{\frac {1}{|x|{\sqrt {x^{2}-1}}}}}$