قواعد الاشتقاق
فيما يلي سرد بمشتقات كثير من الدوال الرياضية. على اعتبار و دالتين قابلتين للاشتقاق، من أعداد حقيقية، وعدد حقيقي ثابت. وهذه الصيغ تكفي لاشتقاق أي دالة أساسية.[1][2]
| جزء من سلسلة مقالات حول |
| التفاضل والتكامل |
|---|
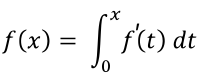 |
|
حساب التكامل |
|
حساب المتسلسلات
|
|
حساب المتجهات
|
|
حساب متعدد المتغيرات |
| بوابة رياضيات |
قواعد التفاضل العامة
قاعدة الضرب
اشتقاق دالة هي عبارة عن حاصل ضرب دالتين يساوي الأولى ضرب مشتقة الثانية + الثانية ضرب مشتقة الأولى.
قاعدة القسمة
في حالة الضرب
إن كانت
فيمكن أخذ لوغاريتم طبيعي للجانبين:
من خصائص اللوغاريتمات أن لوغاريتم مضروبين يساوي مجموع لوغاريتم كل منهما ، إذًا بتطبيق هذه الخاصية تصير الصيغة:
باشتقاق الجانبين ضمنيًّا:
بضرب الجانبين في :
ثم يعوض بقيمة التي هي الدالة الأساسية :
بالضرب واختصار الكسور:
في حالة القسمة
ينطبق ما سبق في حالة القسمة، بيد أنه في القسمة يساوي لوغاريتم مقسوم عددين مطروح لوغاريتم كل منهما ، ويمكن استخدام الطريقة السابقة لاشتقاق الدوال المكونة من مضروب و/أو مقسوم دالتين فأكثر.
قاعدة المقلوب
قاعدة التسلسل
مشتقة الدالة المعكوسة
لأي دالة قابلة للتفاضل f لها قيم حقيقية، عندما تتواجد مركباتها ومعكوساتها.
اعلم بأن المقلوب هو المعكوس في كل الدوال إلا الدوال المثلثية إذ إن معكوساتها ليست مقلوباتها، فمعكوس الدالة المثلثية ينتج الزاوية من قيمة دالة مثلثية عندها.
قاعدة الأس العامة
مشتقات الدوال البسيطة
- حيث كلا من و هي دوال معرفة
مشتقات الدوال الأسية
المعادلة السابقة صحيحة لأي c، ولكن ينتج عن التكامل عدد مركب.
المعادلة السابقة صحيحة أيضا لأي c، ولكن ينتج عن التكامل عدد مركب.
مشتقات الدوال الزائدية
انظر أيضًا
المراجع
- Calculus (5th edition), F. Ayres, E. Mendelson, Schaum's Outline Series, 2009, (ردمك 978-0-07-150861-2).
- Advanced Calculus (3rd edition), R. Wrede, M.R. Spiegel, Schaum's Outline Series, 2010, (ردمك 978-0-07-162366-7).
- بوابة رياضيات
