تكامل معتل
الصيغة الأساسية بأن يكون على أحد الشكلين التاليين:
| جزء من سلسلة مقالات حول |
| التفاضل والتكامل |
|---|
 |
|
حساب التكامل |
|
حساب المتسلسلات
|
|
حساب المتجهات
|
|
حساب متعدد المتغيرات |
| بوابة رياضيات |
أو
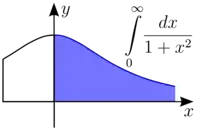
التكامل المعتل حالة الفترة غير المحدودة
إذا كان لدينا تكامل الدالة على الفترة [1, ∞) وهي فتره غير محدوده، فهذا يكون تكامل معتل، ونستخدم الطريقة التالية لحله
نستخدم Lim أو نهاية b إلى مالا نهايه، ونحول فترة التكامل من 1 إلى b ونكامل بالطريقة العادية وفي حال كانت الإجابة رقم ثابت فهو تكامل تقاربي، أما إن كانت الإجابة موجب أو سالب مالا نهايه فالتكامل تباعدي.
حالة فترة غير المحدودة (-∞,∞)
لدينا تكامل معتل على الفترة (-∞,∞)
نقوم بتجزيئة إلى فترتين (-∞,0) و(0,∞) لينتج لدينا تكاملين منفصلين لنفس الدالة
ثم نستخدم طريقة حل التكامل المعتل لكل فترة على حده
- =
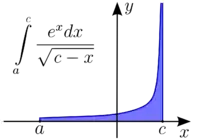
التكامل المعتل حالة الدالة غير المحدودة
باعتبار c هو عدد ثابت تكون الدالة غير معرفه عنده
يكون حل التكامل على الشكل
مثال
لدينا 0 هنا هو c في الشرح السابق حيث تكون الدالة غير معرفه عنده 0
ونلاحظ علامة + فوق الصفر، لأن التكامل غير معرف عند أو تحت الصفر ولكنه معرف عند اي رقم آخر أكبر من 0
مصادر
راجع كتاب مبادئ التفاضل والتكامل الجزء الثاني، د.صالح السنوسي وآخرون، جامعة الملك سعود بالرياض، دار الخريجي للنشر والتوزيع
- بوابة رياضيات
- بوابة تحليل رياضي
