دالة الظل الزائدية
الظل الزائدي (بالإنجليزية: Hyperbolic Tangent) في الرياضيات، هو نوع من أنواع الدوال الزائدية الذي يتميز بخواص معينة، ومجال تعريف محدد وما إلى ذلك من مميزات كل دالة رياضية.
| ظل زائدي | |
|---|---|
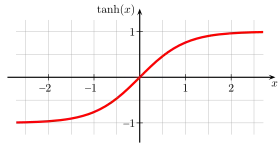 الرسم البياني لدالة الظل الزائدي على جزء من ℝ. الرسم البياني لدالة الظل الزائدي على جزء من ℝ. | |
| ترميز | |
| دالة عكسية | |
| مشتق الدالة | أو |
| مشتق عكسي (تكامل) |
|
| الميزات الأساسية | |
| زوجية أم فردية؟ | فردية |
| مجال الدالة | |
| المجال المقابل | |
| دورة الدالة | iπ |
| قيم محددة | |
| القيمة/النهاية عند الصفر | 0 |
| نهاية الدالة عند +∞ | 1 |
| نهاية الدالة عند -∞ | -1 |
| جذور الدالة | 0 |
| نقاط ثابتة | 0 |
تعريف
يُرمز لدالة الظل الزائدي بالرمز tanh [1] وهي دالة تتكون من أعداد مركبة على النحو التالي :
حيث هي دالة الجيب الزائدي، و هي دالة جيب التمام الزائدي. هذا التعريف هو مماثل لتعريف الدوال المثلثية على غرار تعريف الجيب وجيب التمام، وعلاوة على ذلك أو .
يُمكن التعبير عن دالة الظل الزائدي باستخدام الدالة الأسية وذلك بالشكل التالي:
خصائص
الخصائص العامة
- على مجال تعريف الدالة تكون tanh دالة تامة الشكل (هذا يعني أنها متصلة وقابلة للاشتقاق إلى ما لا نهاية)، في حين تكون مشتقتها الأولى تساوي:
- tanh إذن هو حل للمعادلة التفاضلية
- دالة Tanh هي دالة دورية بمقدار iπ.
- دالة Tanh هي دالة فردية.
- تُمكن هذه الدالة من التحقق من قيمة الدالة الزائدية، حيث أن:
- عند القيام بتطبيق للدالة على المجال ℝ، فإن دالتها العكسية في نفس المجال (ℝ) تكون مُعرفة على ]-1, 1[.
الدالة في سلسلة تايلور
يمكن التعبير عن دالة Tanh في سلسلة تايلور في 0 بمساعدة أعداد بيرنولي، وذلك من خلال العلاقة التالية:
- {{خطأ رياضيات (خطأ في الصياغة): {\displaystyle �rac z{{ m e}^z-1}=\sum_{k=0}^{\infty}B_k�rac{z^k}{k!}=1-�rac z2+\sum_{n=1}^{\infty}B_{2n}�rac{z^{2n}}{(2n)!}.} }}
الدالة في الكسور المستمرة
في 1761، برهن وأثبت يوهان هاينغيش لامبرت أن أحد الحلول في الكسور المستمرة المعممة للدالة tanh هي:
كما أكد على أن النظرية العامة تُمَكِّنُ من استنتاج الدالة الأسية لأي عدد كسري (باستثناء الصفر).
القيم
هذه بعض قيم دالة الـ tanh:
الجذور
الدالة Tanh لها جذر حقيقي وجذور خيالية محضة حيث: .
الدالة العكسية

الدالة العكسية لدالة tanh في المجال ℝ يُرمز لها بـ artanh (أو argtanh أو argth)[2]، ويُمكن تفسيرها بالعلاقة التالية:
حيث ln ترمز للوغاريتم الطبيعي.
بصفة عامة، دالة tanh لها دالة عكسية معرفة على ℝ+i]–π/2, π/2[ في ℂ\(]–∞, –1]∪[1, +∞[)، بحيث:
حيث Log يعني العامل المحدد الرئيسي في اللوغاريتم العُقدي.
بشكل أكثر دقة، لكل z من مجال تعريف الدالة tanh، العدد المركب tanh(z) هو صورة u = e2z من خلال الدالة u ↦ v = (u – 1)/(u + 1). ومع ذلك، فإن هذه الدالة هي مقابلة لـ ℂ\{-1} في ℂ\{1} ومنه فإن v ↦ u = (1 + ت)/(1 – v) إذن ℂ\ℝ– على ℂ\(]–∞, –1]∪[1, +∞[).
التطبيقات
دالة الظل الزائدي هي دالة تمر قيمها تدريجيا ما بين -1 و1، وبالتالي فإنه يمكن استخدامها لتمثيل ظاهرة الانتقال التدريجي أو شيء من هذا القبيل.
بعض الظواهر (الفيزيائية والاقتصادية ...) لا يمكن وصفها من خلال دراسة دالة واحدة على مجال كامل، هذا هو الحال عادة عند دراسة حرارة مادة معينة تمر بالعديد من التغييرات في فترة زمنية محددة، مما يضطر الدارس إلى تحديد مجالين للتعريف (أو أكثر)، مع شرط أن تكون الدالتين مختلفتين في كل مجال، والملاحظ أنه يمكن للدالتين (أو للدوال) أن تكونا من نفس النوع ولكن بقيم مختلفة، وبالتالي نحصل على دالة من نوع:
القيمة xt هي قيمة ثابتة.
في الذكاء الاصطناعي
دالة الظل الزائدي هي أيضا مشابهة جدا لما يحدث في الانتشار الخلفي مع الشبكة العصبونية الاصطناعية والتي لها سمات الدالة القابلة للاشتقاق.
انظر أيضا
الملاحظات والمراجع
- القياسية الدولية ISO 80000-2:2009 توصي tanh
- في معيار ISO ISO 80000-2 [الإنجليزية] توصي artanh.
- بوابة رياضيات
- بوابة تحليل رياضي