قاطع التمام

في علم المثلثات والتحليل الرياضي، دالة قاطع تمام زاوية (بالإنجليزية: Cosecant of an angle)‏ هي إحدى الدوال المثلثية التي تتبع قيمة زاوية ويرمز له بـ: ${\displaystyle {\csc(x)}}$ [3] أو ${\displaystyle \operatorname {cosec} (x)}$، ويمثل القاطع التمام مقلوب قيمة الجيب أي ${\displaystyle \operatorname {csc} \;x={\frac {1}{\sin x}}}$.[3] أي أنه إذا كانت لدينا زاوية ضمن مثلث قائم فإن قاطع تمام هذه الزاوية يساوي نسبة طول الوتر إلى الضلع المقابل للزاوية.

لمعانٍ أخرى، انظر قاطع (توضيح).

قاطع التمام
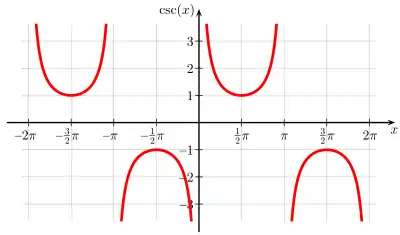تمثيل دالة قاطع التمام في جملة الإحداثيات الديكارتيّة
ترميز	${\displaystyle {\csc(x)}}$
تعريف الدالة	${\displaystyle \csc(x)={\frac {1}{\sin(x)}}}$
دالة عكسية	${\displaystyle {\operatorname {arccsc}(x)}}$
مشتق الدالة	$${\displaystyle {\frac {-\cos \,x}{\sin ^{2}x}}=-\csc x\cdot \cot x}$$ [1]
مشتق عكسي (تكامل)	${\displaystyle {\begin{aligned}-\ln |\csc(x)+\cot(x)|\\=\ln \left|\tan \left({\frac {x}{2}}\right)\right|\end{aligned}}}$[2]
الميزات الأساسية
زوجية أم فردية؟	فردية
مجال الدالة	${\displaystyle \mathbb {R} -\left\{k\pi \right\}}$
المجال المقابل	${\displaystyle ]-\infty ,-1]\cup [1,+\infty [}$
دورة الدالة	2π
قيم محددة
القيمة/النهاية عند ${\displaystyle {\frac {\pi }{2}}}$	1
القيمة/النهاية عند 2kπ	على اليمين: +∞ على اليسار: -∞
القيمة/النهاية عند ${\displaystyle {\pi }+2k\pi }$	على اليمين: -∞ على اليسار: +∞
خطوط مقاربة	${\displaystyle x=k\pi }$
نقاط حرجة	${\displaystyle {\frac {\pi }{2}}+k\pi }$
ملاحظات	${\displaystyle k\in \mathbb {Z} }$

إن القاطع التمام هو دالة مثلثية فرعية نسبية إلى كون الدوال الرئيسية المعروفة هي الجيب وجيب التمام والظل.

يمكن التعبير عن قاطع تمام الزاوية لزاوية x -معبرا عنها بالتقدير الدائري- بواسطة متسلسلة لورنت التالية:[3]

${\displaystyle {\begin{aligned}\csc x&{}=\sum _{n=0}^{\infty }{\frac {(-1)^{n+1}2\left(2^{2n-1}-1\right)B_{2n}x^{2n-1}}{(2n)!}}\\&{}=x^{-1}+{\frac {1}{6}}x+{\frac {7}{360}}x^{3}+{\frac {31}{15120}}x^{5}+\cdots ,\qquad {\text{for }}0<|x|<\pi .\end{aligned}}}$

حيث ${\displaystyle B_{n}}$ هو عدد بيرنولي.