جذر تكعيبي

في الرياضيات يرمز للجذر التكعيبي لعدد ما x بالشكل ${\sqrt[{3}]{x}}$ أو x^1/3، وإذا كان الجذر التكعيبي هو العدد a فتكون العلاقة التالية محققة a³ = x.[1][2][3][4]

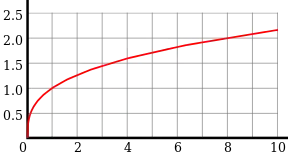
مخطط التابع y =

{\sqrt[{3}]{x}}

من أجل

x\geq 0

. حيث أن المخطط الكامل يكون متناظراً بالنسبة للمبدأ.

لجميع الأعداد الحقيقية جذر تكعيبي حقيقي واحد وجذرين تكعيبيين عقدين.

لجميع الأعداد العقدية غير الصفرية تمتلك ثلاث جذور تكعيبية عقدية.

أمثلة

الجذر التكعيبي للعدد 8 هو 2، لأن 2³ = 8.
الجذور التكعيبية للعدد 27- هي:

{\sqrt[{3}]{-27i}}={\begin{cases}3i\\{\frac {3{\sqrt {3}}}{2}}-{\frac {3}{2}}i\\-{\frac {3{\sqrt {3}}}{2}}-{\frac {3}{2}}i\end{cases}}

خصائص الجذر التكعيبي

عملية الجذر التكعيبي هي عملية غير تجميعية وغير توزيعية مع الجمع والطرح.
عملية الجذر التكعيبي هي عملية تجميعية مع الرفع إلى أس وتوزيعية مع عملية الضرب والقسمة في مجموعة الأعداد الحقيقية، ولكن ليس دائماً في مجموعة الأعداد العقدية.

انظر أيضاً

مراجع

Aryabhatiyaقالب:Lang-mr, Mohan Apte, Pune, India, Rajhans Publications, 2009, p.62, (ردمك 978-81-7434-480-9) ^{[وصلة مكسورة]} نسخة محفوظة 9 مارس 2020 على موقع واي باك مشين.
Smyly, J. Gilbart (1920). "Heron's Formula for Cube Root". Hermathena. Trinity College Dublin. 19 (42): 64–67. JSTOR 23037103. الوسيط |CitationClass= تم تجاهله (مساعدة)
Crossley, John; W.-C. Lun, Anthony (1999). The Nine Chapters on the Mathematical Art: Companion and Commentary. Oxford University Press. صفحة 213. ISBN 978-0-19-853936-0. مؤرشف من الأصل في 26 يناير 2020. الوسيط |CitationClass= تم تجاهله (مساعدة)
خالد (2016-05-17). رفيقُ الأزماتِ لمعالجة الضعف في الرياضياتِ. دار العنقاء. ISBN 9789957573393. مؤرشف من الأصل في 26 يناير 2020. الوسيط |CitationClass= تم تجاهله (مساعدة)

بوابة رياضيات

في كومنز صور وملفات عن: جذر تكعيبي

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.

[1] Aryabhatiyaقالب:Lang-mr, Mohan Apte, Pune, India, Rajhans Publications, 2009, p.62, (ردمك 978-81-7434-480-9) ^{[وصلة مكسورة]} نسخة محفوظة 9 مارس 2020 على موقع واي باك مشين.

[2] Smyly, J. Gilbart (1920). "Heron's Formula for Cube Root". Hermathena. Trinity College Dublin. 19 (42): 64–67. JSTOR 23037103. الوسيط |CitationClass= تم تجاهله (مساعدة)

[3] Crossley, John; W.-C. Lun, Anthony (1999). The Nine Chapters on the Mathematical Art: Companion and Commentary. Oxford University Press. صفحة 213. ISBN 978-0-19-853936-0. مؤرشف من الأصل في 26 يناير 2020. الوسيط |CitationClass= تم تجاهله (مساعدة)

[4] خالد (2016-05-17). رفيقُ الأزماتِ لمعالجة الضعف في الرياضياتِ. دار العنقاء. ISBN 9789957573393. مؤرشف من الأصل في 26 يناير 2020. الوسيط |CitationClass= تم تجاهله (مساعدة)