مقدمة في ميكانيكا الكم

معدن ساخن يتم تشكيله. التوهج الأصفر البرتقالي هو الجزء المرئي من الإشعاع الحراري المنبعث نتيجة ارتفاع درجة الحرارة. الأشياء الأخرى في الصورة متوهجة بأشعة حرارية أيضاً، لكنها أقل توهجاً وذات طول موجي أطول مما يمكن للعين البشرية رؤيته. يمكن رؤية هذا الإشعاع من خلال كاميرا أشعة تحت الحمراء

الإشعاع الحراري هو إشعاع كهرومغناطيسي ينبعث من سطح الجسم ناتج عن درجة حرارته عند تسخين الجسم بما فيه الكفاية، ينبعث منه حينها ضوء من نهاية الطيف الأحمر وهو أحمر شديد الحرارة والاستمرار بتسخين الجسم يؤدي إلى تغيير لونه من الأحمر إلى الأصفر إلى الأبيض ومن ثم إلى أزرق حيث يبدأ الضوء في الانبعاث عند طول الموجات الأقصر (والترددات الأعلى) كما ويتضح أن الأجسام المثالية لإشعاع الضوء هي نفسها الأمثل لامتصاصه عندما تكون باردة فان هذه الأجسام تظهر كاملة السواد حيث أنها تمتص كامل الضوء الساقط عليها ولا ينبعث منها أي منه وبالتالي فإن الجسم ذو الانبعاث الحراري المثالي يُعرف بـ "الجسم الأسود" والإشعاع المنبعث منه يسمى بـ "إشعاع الجسم الأسود". وفي أواخر القرن التاسع عشر، حُددت بوضوح خصائص الإشعاع الحراري عن طريق التجارب*ويشمل قانون إزاحة ويين على كيفية أن الطول الموجي. فحينما يكون الإشعاع في أقوى مراحله، يتغير مع الحرارة يشتمل قانون ستيفان بولتزمان على القوة الشاملة المنبعثة من وحدة مساحة واحدة ولكن لم تتمكن الفيزياء التقليدية من شرح العلاقة بين درجات الحرارة وتردادت الإشعاع السائدة وفي الحقيقة توقعت الفيزياء التقليدية أن الطاقة في الأطوال الموجية القصيرة ستنبعث من خلال جسم ساخن بمعدل لا نهاية له وتعُرف هذه النتيجة بوضوح وهي نتيجة خاطئة تعرف باسم الكارثة فوق البنفسجية وقد بحث الفيزيائيون عن نظرية واحدة تشرح سبب تلقيهم لنتائج تجريبية لم يتوصلوا إليها. وضع العالم ماكس النموذج الأول الذي كان قادراً على شرح مجموعة كاملة من الإشعاع الحراري عام 1900، حيث وضع هذا النموذج بناء على حالة توازن الإشعاع الحراري وذلك باستخدام مجموعة من مؤشرات التذبذب التوافقي ولاستخراج النتائج التجريبية يفترض أن كل مذبذب ينتج عدد صحيح من وحدات الطاقة في ترددها في لحظة واحدة بدلا من أن ترسل كمية من الطاقة بشكل عشوائي وبعبارة أخرى فإن طاقة كل مذبذب تحدد "الكم " لمذبدب نفسه وفقا لبلانك بما يتناسب مع تردد مذبذب ثابت التناسب الذي يعرف باسم ثابت بلانك ويرمز لثابت بلانك ب ( H ) وحيث تقدر قيمته بـ (6,63*10-34j s) وتعطي الطاقة E المذبذب من قبل التردد F ويعتبر قانون بلانك أول قانون فيزيائي لنظرية الكم، حيث حصل العالم بلانك على جائزة نوبل عام 1918 تقديراً لجهوده التي بذلها لنهوض علم الفيزياء وفي ذلك الوقت كانت نظرية العالم بلانك لتحديد الكم خدعة رياضية محضة فضلا عن التغير الجوهري في فهمنا للعالم.

في عام 1905 اتخذ ألبرت آينشتاين خطوة إضافية أشار فيها أن كمية الضوء لم تكن خدعة رياضية حيث أن الطاقة في شعاع الضوء تظهر في حزم فردية والتي تسمى الآن فوتونات [8] وتحسب طاقة الفوتون الواحد عن طريق ضرب التردد بثابت بلانك وقد تجادل العلماء لعدة قرون بين نظريتين محتملتين للضوء: هل هو موجة أم تيار من الجسيمات الصغيرة؟ وبحلول القرن التاسع عشر تم تسوية الجدال بشكل عام لصالح نظرية الموجة حيث كانت قادرة على تفسير آثار ملحوظة كانكسار وانحراف الضوء والاستقطاب وقد بين جيمس كليرك ماكسويل أن كلًا من الكهرباء والمغناطيس والضوء مظاهر لنفس ظاهرة الحقل الكهرومغناطيسي وتصف معادلات ماكسويل والتي هي مجموعة كاملة من قوانين الكهرومغناطيسية الكلاسيكية الضوء على أنها موجات مجموعة من الحقول الإلكترونية والمغناطيسية المتذبذبة وبسبب رجحان الأدلة لصالح نظرية الموجة فإن فكرة إنشتاين التقت مبدئيًا بشكوك هائلة ولكن وفي نهاية المطاف أصبح نموذج الفوتون محبذًا وكان أحد الأدلة المهمة لصالحه هو قدرته على تفسير عدد من الخصائص المحيرة للتأثير الكهروضوئي والذي سيتم وصفه في القسم التالي ومع ذلك ظل تشبيه الموجة أساسيًا لا غنى عنه لمساعدته في فهم خصائص أخرى للضوء كانحراف الضوء.

التأثير الكهروضوئي

يشع الضوء (الأسهم الحمراء، يساراً) فوق المعدن. إذا كان الضوء ذا تردد ٍ كافٍ (أي طاقة كافية)، فإن الإلكترونات تنطلق (الأسهم الزرقاء، يمين).

•  مقالة مفصلة: التأثير الكهروضوئي

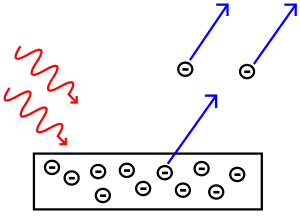
في عام 1887 لاحظ هاينريش هيرتس أن باستطاعة الضوء إطلاق الإلكترونات من المعدن.[3] وفي عام 1902 اكتشف فيليب أنتون لينارد أن الطاقة القصوى الممكنة للإلكترون الخارج أو المطرود ترتبط بتردد الضوء لا بشدته، فإذا كان التردد منخفضًا جدًا فلا يطرد أي إلكترون بغض النظر عن شدة الضوء ويسمى أقل تردد للضوء والذي يجعل الإلكترونات تنبعث من المعدن تردد العتبة ويختلف من معدن لآخر. وهذه الملاحظة على خلاف مع الكهرومغناطيسية الكلاسيكية التي تتنبأ بأن طاقة الإلكترون يجب أن تكون متناسبة مع شدة الإشعاع.[4]

فسّر أينشتاين ذلك التأثير بافتراض أن حزمةً من الضوء هي عبارة عن تيار من الجسيمات (فوتونات)، فلو كان تردد هذه الحزمة f فإن طاقة كل واحد من هذه الفوتونات تعادل hf.[3] فمن المحتمل أن يصطدم الإلكترون بفوتون واحد فقط والذي غالباً ما ينقل طاقة hfإلى الإلكترون[3]؛ وبناء على ذلك فإن لا يكون هناك تأثير لشدة هذه الحزم الضوئية ليس لها أي تأثر، فقط ترددها هو من يحدد الطاقة القصوى التي يمكن نقلها إلى الإلكترون.[3] ولشرح تأثير العتبة، قال إينشتاين بأن إطلاق إلكترون من معدن يحتاج إلى كمية معينة من الطاقة يرمز لها بـ φ.[3] تختلف كمية هذه الطاقة باختلاف نوع المعدن وإذا كانت طاقة الفوتون أقل من وظيفة العمل فحينها يكون لا يحمل طاقة كافية لإطلاق الإلكترون من المعدن وتردد العتبة f₀ هو تردد الفوتون الذي طاقته مساوية لوظيفة العمل.

وإذا كان f أكبر من f0 فتكون طاقة hf كافية لإطلاق الإلكترون ويحمل الإلكترون المقذوف طاقة متحركة EK والتي غالبًا ما تكون مساوية لطاقة الفوتون ناقص الطاقة اللازمة لطرد الإلكترون من المعدن. وصف أينشتاين للضوء على أنه يتكون من جزيئات تعزز فكرة بلانك للطاقة الكمية: حيث أن الفوتون الواحد من تردد معطى د ينقل كمية ثابتة من الطاقة هـ د. بمعنى آخر فإن الفوتون الواحد يستطيع نقل طاقة أكثر أو أقل وذلك يعتمد على تردده فقط وبالرغم من أن الفوتون جزيء لكنه يوصف على أنه يحمل خصائص الترددات الموجية ومرة أخرى تم تسوية حساب جزيئات الضوء [10].

العلاقة ما بين تردد الإشعاع الكهرومغناطيسي وطاقة كل الفوتون الواحد هي السبب في أن الأشعة فوق البنفسجية يمكنها أن تسبب ضربة الشمس وهذا ما لا يمكن للضوء المرئي أو للأشعة تحت الحمراء فعله يمكن لفوتون الأشعة الفوق البنفسجية أن يولد كمية عالية من الطاقة تكفي في أن تساهم في تلف الخلايا مثل ما يحدث في ضربة الشمس.

أما فوتون ضوء الأشعة تحت الحمراء فهو يولد كمية أقل من الطاقة مما يكفي لتدفئة الجلد فقط فلذل، يمكن لمصباح الأشعة تحت الحمراء أن يقوم بتدفئة سطح كبير يكفي لجعل الناس يشعرون بالراحة في غرفة باردة ولكن لا يمكنه أن يسبب ضربة الشمس لأي شخص. إذا كان كل فوتون منفرد له طاقة متطابقة فليس من الصواب الحديث عن "الطاقة العالية" للفوتون، الضوء ذو التردد العالي قد يحمل طاقة أكثر فقط لفيضان السطح بوصول فوتونات أكثر في الثانية الواحدة، الضوء ذو التردد المنخفض قد يستطيع حمل طاقة أكثر للسبب عينة، إذا كان ذلك صحيحًا أن كل الفوتونات تحمل نفس الطاقة فإنك لو ضاعفت نسبة وصول الفوتون ستضاعف عدد وحدات الطاقة التي تصل في الثانية الواحدة.

رفض إينشتاين النهج التقليدي المعتمد على الموجة بتأييده للتحليل القائم على الجسيمات حيث أن طاقة الجسيم قطعًا تختلف تبعًا للتردد في خطوات منفصلة (مكماة) كل الفوتونات ذات التردد نفسه لها طاقة متطابقة وكل الفوتونات ذات الترددات المختلفة لها طاقات مختلفة بالتناسب مع ترددها.

في الطبيعة ونادرًا ما تصادف الفوتونات الفردية، الشمس تبعث الفوتونات بشكل مستمر في جميع الترددات الكهرومغناطيسية لذلك يبدو أنها تنتشر كموجة مستمرة وليس كوحدات منفصلة، مصادر الانبعاثات المتاحة لهيرتز وينارد في القرن التاسع عشر شاركت هذه الخاصية، فنجم يشع ضوءا أحمر أو قطعة حديد في حداد تشع بإحمرار يمكن أن نقول عنهما أنهما يحتويان على قدر كبير من الطاقة. يمكن التخمين بأن إضافة الاستمرارية لمجموع الطاقة لبعض الأجسام المشعة يجعلها تُشع ضوءاً أحمر، ضوءاً برتقالي، ضوءً أصفرا، َضوءً أخضر، ضوءً أزرق، ضوءً بنفسجي، وهلم جرًا بهذا النظام

ولكنها ليست على هذة الشاكلة فالنجوم الكبيرة والقطع الحديدة الكبيرة في الحدادة حينها من الضروري أن تتوهج بألوان أكثر قربة نحو البنفسجي نهاية الطيف لتغير لون جسم مشع مِماثل من الضروري أن تغير حرارتة، إن الازدياد في الحرارة تٌغِير حصة الطاقة المتاحة لتحفيز الذرات الاحادية لمستويات أعلى تمكنهم من بعث فوتونات بترددات عالية.

في مطلع القرن العشرين، تطلب برهان وجود المادة نموذجاً للذرة مع سحابة من الإلكترونات السالبة المنتشرة والتي تحيط بنواة صغيرة عالية الكثافة وموجبة الشحنة ولأجل هذه الخصائص تم اقتراح نموذج تدور فيه الإلكترونات حول النواة كما تدور الكواكب حول الشمس.

ملاحظة 5] ومع ذلك، كان من المعروف أيضا أن الذرة في هذا النموذج ستكون غير مستقرة]

وفقا للنظرية الكلاسيكية (التقليدية) في هذا الشأن التي ترى أن الإلكترونات الدوارة تخضع لتسارع الجاذبية وبالتالي فإنها تطلق الإشعاع الكهرومغناطيسي، كما أن فقدان الطاقة يؤدي إلى التوجه في دوامة نحو النواة عندها يحدث الاصطدام بها في جزء من الثانية.

الحيرة الثانية المتعلقة بها كانت في الإشعاعات الطيفية للذرات فعندما يسخن الغاز تطلق الضوء ولكن في ترددات منفصلة مثلا الضوء المرئي المطلق من الهيدورجين يحتوي على أربعة ألون مختلفة كما هو موضح في الصورة أدناه بينما في المقابل الضوء الأبيض يحتوي على إشعاعات مستمرة بلا انقطاع عبر نطاق الترددات المرئية.

نموذج بور للذرة، يبّين إلكترون من مدار واحد، ينتقل من مدار إلى آخر عن طريق انبعاث فوتون.

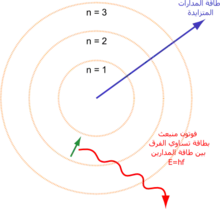
في عام 1913، قدّم نيلز بور نموذجاً جديداً للذرة يشمل مدارات الإلكترون المكممة، ولا تزال الإلكترونات في نموذج بوهر تدور حول النواة بقدر الكواكب التي تدور حول الشمس ويُسمح لها بالتواجد في مدارات معينة فقط وليس في أي مدار أو على أي مسافة.[5] إن الذرة عندما تبعث أو تمتص الطاقة، فإن الإلكترونات لا تتحرك في مسار مستمر من مدار واحد حول النواة إلى آخر كما هو متوقع بشكل تقليدي، بدلاً من ذلك فإن الإلكترون يقفز من مدار إلى آخر على الفور ويُطلق الضوء المنبعث على هيئة فوتون[6]، يتم تحديد الطاقات الممكنة من الفوتونات التي تخرج من كل عنصر على حسب الاختلافات في الطاقة بين المدارات وبالتالي فإن طيف الانبعاث لكل عنصر من شأنه أن يحتوي على عدد من الخطوط.[7]

نيلز بور في شبابه

كان نموذج بور قادرًا على ربط الخطوط الطيفية المرصودة في انبعاثات الطيف للهيدروجين بالكميات الثابتة المعروفة مسبقاً، بالرغم من أن هذا النموذج لم يوضح لماذا يجب أن تكون المدارات مكممة بتلك الطريقة وكان نموذج بور غير قادر أيضاً على وضع توقعات دقيقة لذرات الإلكترونات المتعددة أو لشرح لماذا بعض الخطوط الطيفية أكثر سطوعاً من غيرها ومع مرور الوقت تم إدراك الطريقة التي تسلكها الإلكترونات بأنها مختلفة بشكل يلفت النظر عن ذرة بور وكذلك عن ما نشاهده في العالم من تجاربنا اليومية وهذا ما تم مناقشته في الأسفل عن الكم الحديث للنموذج الميكانيكي في الذرة.

عام 1923 اقترح لويس دي بروي فكرة أنه كما أن للضوء خصائص كلاً من الموجات والجسيمات معاً فإن للمادة أيضاً خصائص الموجات [16]، الطول الموجي λ المتعلق بجسيمٍ ما مرتبط بكمية حركته p من خلال ثابت بلانك h :[17][18] تنطبق العلاقة السابقة (والتي سُميت بفرضية دي بروي) على كل أنواع المادة ولذلك فإن كل المواد تمتلك خصائص كلاً من الجسيمات والموجات، بعد 3 سنوات تم الكشف عن طبيعة الإلكترون المشابهة للموجات عن طريق إظهار أن شعاع من الإلكترونات يمكنه الحيود (الانحراف) تماماً مثل شعاع الضوء.

في جامعة أبردين قام جورج ثومسون بتمرير شعاع من الإلكترونات عبر طبقة معدنية رقيقة ولاحظ أنماط الحيود المتوقعة وفي مختبرات بل قام كلاً من دافيسون وجيرمر بتمرير شعاع من الإلكترونات عبر شبكات كريستالية، تم لاحقاً الكشف عن ظواهر مشابهة في الذرات وحتى في الجزيئات الصغيرة حيث تمتلك خصائص الموجات أيضاً، مُنح دي بروي جائزة نوبل للفيزياء عام 1929 عن فرضيته، كما تقاسم ثومسون ودافيسون جائزة نوبل للفيزياء عام 1937 لتجاربهم المتعلقة بهذا المجال.

مبدأ ازدواجية الموجة-الجسيم يُظهِر أن المفهوم الكلاسيكي لنظرية "الجسيمات" و"الموجات" لايمكنه وصف سلوك المواد (سواء كانت جسيمات أو فوتونات) على المستوى الكمي بشكل كامل ودقيق ولذا فإن ازدواجية الموجة-الجسيم هو مثال على مبدأ التكامل principle of complementarity في فيزياء الكم سوف يتم مناقشة مبدأ ازدواجية الموجة-الجسيم من خلال تجربة شقي يونغ Double-slit experiment في الفقرة التالية. لا يمكن للمفهوم الكلاسيكي للجسيمات أو للموجات أن يصف مفهوم موجة-الجسيمات الازدواجية بشكل متكامل لسلوك كائنات الكم بكلا الحالتين: كفوتون أو كمادة، في الواقع اقترح عالم الفيزياء أي إس إيدينغتون في عام 1927 أنه " بإمكاننا أن نصف هذا الكيان كموجة أو كجسيم وربما كحل وسط ينبغي أن نطلق عليه" [Wavicle". [20 (هذا المصطلح اشتهر لاحقاً عن طريق الرياضي بانيش هوفمان)[21]:172، موجة الجسيمات الازدواجية هي مثال على مبدأ ازدواجية الجسيمات في الكم الفيزيائي ومثال فريد لموجة الجسيمات الازدواجية وهي تجربة الشقين، ستتم مناقشتها في الجزء السفلي فمعالجة الدكتور بروغلي لأحداث الكم هي النقطة البدء لشوردينغر عندما أنشئ معادلة الموجة لشرح أحداث الكم النظرية.

قام إروين شرودنغر في عام 1925 بناءً على فرضية دي برولي بتطوير المعادلة التي تصف سلوك الموجة الميكانيكية الكميّة وتعد المعادلة التي يطلق عليها معادلة شرودنجر نسبة للعالم الذي اكتشفه، أساسية لميكانيكا الكم، فهي تعرّف الحالات المستقرّة للنظام الكمّي وتصف كيف تتغير الحالة الكمية للنظام الفيزيائي عبر الزمن[9] وذكر في الأطروحة التي قدّمت قطة شرودنجر أن وظيفة الدالة الموجبة Ψ في معادلته هي تقديم "وسائل التنبؤ للتوقعات المحتملة لنتائج القياسات"، وبالتالي توفير "التوقعات المستقبلية كما تم وضعها في الكتالوج إلى حد ما." [24] وكان سكرودنغ قادرا على حساب مستويات الطاقة في الهيدرجوين وذلك بمعالجة إلكترون ذرة الهيدروجين كموجة كلاسيكي متحركا داخل جدارا من الجهد الكهربي بفعل البروتين.وتعيد هذه العملية إنتاج مستويات طاقة نموذج بوهر. كان ورنر هايزنبرغ في زمن سابق يحاول إيجاد تفسير للاختلافات الموجودة في قوة انبعاث طيف الهيدروجين بسلسة من التماثلات الرياضية إذ كتب عن قوة التماثلات الميكانيكية الكمية، بعد ذلك بوقت قصير أدرك زميله ماكس بورن أن طريقة هايزنبرغ في حساب احتمالات انتقال مستويات الطاقة المختلفة يمكن أن يفسر أفضل باستخدام مفهوم المصفوفات. في مايو 1926، أثبت شارودنغر أن نظريتي هايزنبيرغ لميكانيكا المصفوفات وميكانيكيا الموجة في التنبؤ بخصائص وسلوكيات الإلكترون متطابقتان رياضياً، لكن مع ذلك لم يتفق شارودنغر وهايزنبيرغ على التفسير المشترك للنظرية فهايزنبيرغ مثلاً لا يرى أي مشكلة في فرضية الانتقال الفوري للإلكترونات بين المدارات في الذرة، بينما كان شارودنغر يأمل بأن تتجنب النظرية القائمة على خصائص الموجة الطولية ما أسماه (القفزات الكمية حول النواة) والتي أقتبست من قبلفلهلم فيين [10][10]

حاول بور وهايزنبيرغ وآخرين تفسير ما تعنيه نتائج هذه التجارب والنماذج الرياضية، كان وصفهم والذي اشتُهر بـ "تأويل كوبنهاغن لميكانيكا الكم" يهدف إلى شرح الطبيعة الحقيقية والتي كانت تٌبحث عن طريق القياسات وتُوصف عن طريق معادلات رياضية لميكانيكا الكم.

المبادئ الأساسية لتفسير كوبنهاغن هي:

1. يوصف النظام كلياً بواسطة دالة الموجة Ψ. (هايزنبرج)
2. كيفية تغير Ψ عبر الزمن معطاة بواسطة معادلة شرودنجر.
3. وصف الطبيعة هو قائم على الاحتمالات أساساً، فاحتمالية حدث ما - على سبيل المثال أين سيظهر الجسيم على الشاشة في تجربة الشقين - مرتبطة بمربع القيمة المطلقة للسعة التي في معادلة الموجة (قاعدة بورن، نسبة إلى ماكس بورن، التي تعطي معنى لمعادلة الموجة في تفسير كوبنهاغن: مبدأ الشك)
4. إنه من غير الممكن معرفة قيم كل الخصائص للنظام في نفس الوقت هذه الخصائص الغير معروفة بدقة يجب أن توصف بالاحتمالات. (مبدأ الشك لهايزنبرج)
5. المادة كالطاقة تظهر إزداوجية الموجة - الجسيم فيمكن لتجربة ما أن تستعرض الخصائص الجسيمية للمادة أو خصائصها الموجية لكن لا تستطيع استعراض كلتيهما في نفس الوقت (مبدأ التكامل لـ بور).
6. أدوات القياس هي أساساً أدوات كلاسيكية وتقيس خصائص كلاسيكية كالموضع وقوة الحركة.
7. الوصف الميكانيكي الكمي لنظام كبير ينبغي أن يكون قريباً جداً من الوصف الكلاسيكي. (مبدأ التوافق لـ بور وهايزنبرج)

تم مناقشة عدة نتائج لهذه المبادئ بالتفصيل في الأقسام الفرعية التالية.

في عام 1928 قام بول ديراك بتطوير وإعادة صياغة معادلة باولي التي وصفت نشاط الإلكترونات لحساب النظرية النسبية الخاصة، ظهرت النتيجة كنظرية تعاملت بشكل مناسب مع الأحداث فعلى سبيل المثال قدرت سرعة الإلكترون حول مدار النواة في جزء كبير من سرعة الضوء وقام ديراك باستخدام أبسط التفاعلات الكهرومغناطيسي وكان قادراً على التنبؤ بقيمة العزم المغناطيسي المرتبط بدوران الإلكترون حيث وجدا قيمتها الفعلية والتي كانت كبيرة جداُ لتكون في نطاق تحكم الفيزياء الكلاسيكية وكان قادراً على حل الخطوط الطيفية لذرة الهيدروجين وعلى إمكانية التكاثر نسبةً لمبادئ الجسدية الأولى لمعادلة سمرفلد الناجحة لإنتاج تركيبة دقيقة من طيف الهيدروجين.

أسفرت معادلات ديراك في بعض الأحيان عن قيمة سالبة للحصول على الطاقة فقد اقترح حلًا لـ الرواية وقال أنه افترض وجود ضديدي الإلكترون وفراغ الديناميكية مما أدى إلى نظرية الحقل الكمومي عديد الجسيمات.

المقال الرئيسي: التشابك الكمي

ينص مبدأ باولي للاستبعاد على أنه لا يمكن لإلكترونين في نفس النظام أن تكون لهم نفس الحالة، الطبيعة -على أي حال- تترك الاحتمالية مفتوحة لأن يكون للإلكترونين كلا الحالتين "متداخلة" على كل واحد منهم، نستذكر أن دوال الموجة التي تنشأ في نفس اللحظة من شقين إثنين تصل إلى شاشة الكشف في حالة تراكب فلا شئ مؤكد مالم تنهار الأشكال الموجية المتراكبة ففي تلك اللحظة يبرز إلكترون في مكان ما حسب الاحتمالية التي هي مربع القيمة المطلقة لمجموع السعات ذات القيم المركبة للشكلين الموجيين المتراكبين فالحالة هناك هي تصورية جدا حالياً فهي طريقة محددة في التفكير عن الفوتونات المتشابكة الفوتونات حيث تتراكب حالتان متضادتان إثنتان على كل منهما في نفس الحدث هي كما يلي:

تخيل أن تركيب حالتين يمكن وصفهما ذهنياً باللون الأزرق والآخر باللون الأحمر فسوف يظهر (تخيلياً طبعاً) كحالة أرجوانية ولنفترض أيضاً أن الفوتونان نتجا عن نفس الحدث الذري وقد يكون تكونهما ناتج عن إثارة كريستالة لديها خاصية امتصاص فوتون ذو تردد معين ومن ثم إصدار فوتونان لديهما نصف التردد الأصلي لذا فكلا الفوتونين يكونان بالحالة الأرجوانية.

إذا ما قام المختبر ببعض التجارب لتحديد كون أحد الفوتونات أحمر أو أزرق فإن هذه التجربة تغير حالة الفوتون المعني من كونه يمتلك حالة تراكب من "الأحمر" و"الأزرق" إلى فوتون لديه واحد فقط من هذه الصفات كانت المشكلة التي عانى منها اينشتاين مع هذه الحالة التخيلية هي أنه إذا كان أحد هذه الفوتونين في حالة ارتداد مستمر بين مرايا متعددة في مختبرعلى كوكب الأرض وقطع الفوتون الثاني نصف مسافة الطريق إلى أقرب نجم خارجي فعندما يتم الكشف عن الفوتون الأول بكونه أزرق أو أحمر فهذا يعني أن الفوتون البعيد عليه أيضا ً ان يفقد حالته الأرجوانية فإذا تم اختباره بعد قياس الفوتون التوأم فإنه حتماً سوف يظهر في الحالة المعاكسة لحالة توأمه.

في محاولة لإثبات أن ميكانيكا الكم ليست نظرية كاملة بدأ اينشتاين بالتنبؤ الخاص بالنظرية التي تنص على أن اثنين أو أكثر من الجسيمات التي تفاعلت في الماضي يمكن أن يُظهرا ارتباطاً قوياً عندما يتم قياس خصائصهما المختلفة في وقتٍ لاحق، سعى اينشتاين لتفسير هذا التقاعل بطريقة كلاسيكة أي من خلال ماضيهما المشترك، مفضلاً أن لا يكون التفسير على افتراض "عمل تخيلي عن بعد" وقام كلاً من إينشتاين وبودولسكي وروزن عام 1935 بكتابة ورقة بحثية علمية شهيرة عُرفت اختصاراً بـ(EPR إي-بي-آر نسبة إلى الحروف الأولى لأسمائهم) مفصلة مايُعرف الآن ب"مفارقة إي-بي-آر" EPR paradox والتي استناداً على مايُعرف الآن بالواقعية المحلية تحاول أن تُظهر من خلال النظرية الكمية أن الجسيم يمتلك موضع وكمية حركة في آنٍ معاً على عكس مايفترضه تفسير كوبنهاغن القائل بأنه واحد فقط من هذه الخصائص يمكن أن يتواجد وفقط في اللحظة التي يتم قياسه فيها. تستنتج فرضية إي-بي-آر أن النظرية الكمية غير مكتملة لأنها ترفض الأخذ بالاعتبار الخصائص الفيزيائية التي توجد بشكل مؤثر في الطبيعة (تعد ال إي-بي-آر أحد أكثر فرضيا اينشتاين ذِكراً في مجالات الفيزياء) ففي نفس العام استخدم إرفين شرودنغر Erwin Schrödinger مصطلح "التشابك الكمي" "entanglement" وصرح قائلاً: "لايمكنني أن أصفه بأنه صفة واحدة بل سمة مميزة من سمات ميكانيكا الكم".[31] يظل التساؤل حول ما إذا كان "التشابك الكمي" حالة واقعية محل خلاف وجدل بين العلماء. [32] كما تظل مبرهنة (لاتساويات) بيل Bell inequalities من أكبر التحديات التي تواجه فرضية اينشتاين.

المقال الرئيسي: نظرية الحقل الكمي

بدأت فكرة نظرية الحقل الكمي في أواخر العشرينات حيث قام الفيزيائي البريطاني بول ديراك بمحاولة تحويل التفسير الكلاسيكي للمجال الكهرومغناطيسي إلى التفسير الكمي الميكانيكي وهي عملية لبناء نظرية كمية بدءًا بنظرية كلاسيكية. الحقل في علم الفيزياء: "هو المنطقة أو الحيز التي يوجد بها تأثير معين (مثل التأثير المغناطيسي)"[34] أما الآثار الأخرى التي يُعبَّر عنها بالحقول فهي حقلي الجاذبية والكهرباء الساكنة في عام 2008، كتب الفيزيائي ريتشارد هاموند أنه في بعض الأحيان نميز بين ميكانيكا الكم ونظرية الحقل الكمي حيث تشير ميكانيكا الكم إلى النظام الذي يتم فيه تثبيت عدد من الجسيمات والحقول (مثل الحقل الكهروميكانيكي) هي كائنات كلاسيكية مستمرة أما نظرية الحقل الكمي فتأخذ خطوة أبعد وتسمح بإنشاء وإبادة الجسيمات.

واستطرد قائلًا أن آلية الكمية عادةً ما تستخدم للإشارة إلى " الفكرة العامة لنظرية الكمية". [36]:108

في عام 1931، طرح ديرك فكرة وجود الجسيمات والتي عرفت لاحقًا بالمادة المضادة.[37] كما تقاسم ديرك جائزة نوبل للفيزياء مع شرودنغر " لاكتشاف أشكال إنتاجية جديدة للنظرية الذرية". [38]

الديناميكا الكهربائية الكمومية ( QED) هو اسم لنظرية القوة الكهرومغناطيسية الكمية، فـفهم الديناميكا الكهربائية الكمومية يبدأ بفهم الكهرومغناطيسية، ويمكننا أن نُطلق على الكهرومغناطيسية أيضًا "الديناميكا الكهربائية"؛ وذلك لأنها تفاعل ديناميكيًا بين القوى الكهربائية والمغناطيسية، فالكهرومغناطيسية تبدأ بالشحنة الكهربائية. الشحنات الكهربائية هي مصادر المجالات الكهربائية ومنشأها فالمجال الكهربائي هو مجال يبذل القوة على أي من الجزئيات التي تحمل شحنات كهربائية في أي نقطة في الفضاء، يتضمن ذلك الإلكترون والبروتون وحتى الكواركات من بين الجزيئات الأخرى، عندما تُبذل القوة تتحرك الشحنات الكهربائية فيتدفق التيار وينتج المجال المغناطيسي في المقابل فإن هذا المجال المغناطيسي يسبب تيار كهربائي (الإلكترونات المتحركة) ويسمى هذا التفاعل الكهربائي والمجال المغناظيسي بالمجال الكهرومغناطيسي.

يسمى الوصف الفيزيائي لتفاعل الجزيئات المشحونة والتيارات الكهربائية والمجالات الكهربائية والمغناطيسية بالكهرومغناطيسية.

في عام 1928، أنتج بول ديرك نظرية كمية نسبية للكهرومغناطيسية، كانت هذه أصل الديناميكا الكهربائية الكمية الحديثة التي كانت تمتلك المكونات الأساسية للنظرية الحديثة لكن مشكلة اللانهائيات غير القابلة للحل تطورت في نظرية الحقل الكمومي ، حلت إعادة التطبيع هذه المشكلة في سنوات لاحقة، مبدئيًا كان يُشتبه بأنها إجراء مؤقت من بعض منشئيها، لكن في النهاية تُقُبّلت إعادة التطبيع كأداة مهمة ومتماسكة بذاتها في الديناميكا الكهربائية الكمية وحقول أخرى في الفيزياء كما حاكت رسومات فينمان في أواخر الثلاثينات جميع التفاعلات الممكنة والمرتبطة بحدث معطى وأوضحت الرسومات أن القوة الكهرومغناطيسية هي تفاعلات الفوتونات بين الجزيئات المتفاعلة.

يعتبر" تحول لامب" مثال على التنبؤ بالديناميكا الكهربائية الكمية والذي تم التحقق منه تجريبيًا. يشير ذلك إلى التأثير الذي عن طريقه تتسبب الطبيعة الكمية للمجال الكهرومغناطيسي في انحراف بسيط في مستويات الطاقة في الذرة أو الأيون عن ما كانت ستكون عليه بدون هذا التحول. نتيجة لذلك قد تتحول أو تنقسم الخطوط الطيفية.

في الستينات أدرك الفيزيائيون أن الكهروديناميكية الكمية تتحلل عند طاقات عالية جدًا، ومن هذا التقلّب، تم اكتشاف "النموذج القياسي" لفيزياء الجسيمات الذي عالج تحلل الطاقة الأعلى في النظرية. ويوحد النموذج القياسي التفاعلات الضعيفة والكهرومغناطيسية في نظرية واحدة تسمى "النظرية الكهروضعيفة".

جميعُ القياسات الفيزيائية، والمعادلات والوثائق المُسندة لميكانيكا الكم ثابتة ،وتحملُ مستوىً عالياً من الإثبات. والسؤال الذي تطرحه هذه النماذجُ النظريةُ عن الطبيعةِ في الحياةِ التطبيقيةِ وُجِدت لها إجاباتٌ تنافسية.

تتضمن تطبيقات ميكانيكا الكم الليزر والترانزستور والمجهر الإلكتروني والتصوير بالرنين المغناطيسي، وهناك نوع خاص من تطبيقات الكم الميكانيكية يرتبط بـظواهر المجهر الإلكتروني مثل الهليوم الفائق والموصلات الفائقة. كما أدت دراسة أشباه الموصلات إلى اختراع الصمام الثنائي والترانزستور اللذان يعدان هما أساس الإلكترونيات الحديثة حيث لا يمكن الاستغناء عنهما. وفي ضوء هذه التحولات البسيطة، يعد نفق الكم نفق حيوي، في الجانب الآخر لا يمكن لـلالكترونيات في التيار الكهربائي أن تخترق الحاجز الجهدي المصنوع من طبقة الأكسيد. بالإضافة إلا ذلك، رقائق الذاكرة السريعة الموجودة في محرك الناقل التسلسلي العام أيضًا تستخدم نفق الكم وذلك لمسح خلايا الذاكرة. ملاحظات

الفيزياء الكلاسيكية -أيضًا- لا تصف بدقة الكون على مقاييس أكبر أو عند سرعات قريبة من سرعة الضوء. يتطلب الوصف الدقيق النسبية العامة.

كلمة "كمي" تأتي من الكلمة اللاتينية المقابلة لـ "كم" (و كذلك "الكمية"). الشئ الـ "مكمم"، مثل طاقة مذبذب بلانك الهرموني، يمكن أن تكون له قيم محددة. مثلًا، في أغلب البلدان، المال مكمم فعليًا، حيث "كم المال" هو أقل عملةٍ قيمةً في عملية التداول. "الميكانيكا" هي فرع من العلم يتعامل مع فعل القوى على الأشياء، إذا "ميكانيكا الكم" هو الجزء من الميكانيكا الذي يتعامل مع الأشياء التي لها خصائص معينة مكممة.

حقيقةً، يمكن أن يكون هناك تأثيرات تعتمد على الكثافة، لكن على الكثافات المُتَحصّلة من مصادر غير الليزر فإن هذه التأثيرات غير ملاحظة.

معادلة التأثير الكهروضوئي لآينشتاين يمكن أن تُشتَق وتبين دون الحاجة إلى مفهوم الـ "فوتون". ذلك أن الإشعاع الكهرومغناطيسي يمكن أن يعامل على أنه موجة كهرومغناطيسية كلاسيكية، طالما أن الإلكترونات في المادة تعامل بواسطة قوانين ميكانيكا الكم. كميًا، تكون النتائج صحيحة بالنسبة لمصادر الضوء الحرارية (مثل الشمس، المصابيح المتوهجة .. إلخ) لكل من معدل انبعاث الإلكترون وكذلك توزيعها الزاوي. للمزيد حول هذه النقطة، انظر [12]

يدعى النموذج الكلاسيكي للذرة بالنموذج الكوكبي، أو أحيانًا نموذج رذرفورد تبعًا لإرنيست رذرفورد الذي اقترحه عام 1911، اعتمادًا على تجربة رقاقة الذهب لجيجر ومارسيديان والتي تستعرض أولًا وجود الذرة.

يمكن تعديل النموذج بسهول لاعتبار طيف الانبعاث لأي نظام يتكون من نواة وإلكترون واحد (ذلك أن، الأيونات كـ He+، أيون الهيليوم، أو كـ O7+، أيون الأوكسجين، تحتوي على إلكترون واحد).

لنظرة أكثر تعمقًا لكيفية انتقال هايزنبرج من نظرية الكم القديمة والفيزياء الكلاسيكية إلى ميكانيكا الكم الجديدة، انظر مدخل هايزنبرج لميكانيكا المصفوفات.

• بوابة ميكانيكا الكم
• بوابة الفيزياء