فوتون

نظرية النموذج العياري

النموذج العياري الخلفية فيزياء الجسيمات نظرية الحقل الكمومي نظرية القياس كسر التناظر التلقائي آلية هيغز الأسس تآثر كهروضعيف ديناميكا لونية كمية مصفوفة سي-كي-ام التقييدات فيزياء ما وراء النموذج العياري مسألة التسلسل الهرمي تذبذب النيوترينو العلماء فاينمان · سودارشان · مارشاك · جيلمان · ساكاتا · جلاشو · زفايج · نامبو · هان · كابيبو · واينبرج · عبدالسلام · ماكوتو · هوفت · ماساكاوا · ويلزك · هولتيزر · فيلتمان · غروس ·

أظهرت تجربة الشق المضاعف لتوماس ينغ في 1805 أن الضوء يمكن أن يتصرف مثل الموجة، مساندة بذلك في هزيمة نظريات الجسيم المبكرة للضوء.

كانت أغلب النظريات حتى القرن الثامن عشر تصف الضوء على أنه ناشئ عن جسيمات. أحد هذه النظريات المبكرة كانت قد وصفت في كتاب البصريات (1021) لابن الهيثم، الذي اعتبر أن أشعة الضوء عبارة عن تيارات من جسيمات صغيرة جداً والتي تفتقر لكل المؤهلات الحسية عدا الطاقة.[4] كان هذا رأي إسحاق نيوتن أيضًا في طبيعة الضوء. لما كانت نماذج الجسيم غير قادرة على تفسير الانكسار والحيود والانكسار المزدوج للضوء، فقد اقتراح نظريات الموجة للضوء رينيه ديكارت (1637)، [5] روبرت هوك (1665)، [6] وكريستيان هايغنز (1678);[7]، بالرغم من ذلك، ظلت نماذج الجسيم هي الغالبة، بشكل رئيسي لتأثير إسحاق نيوتن.[8] في أوائل القرن التاسع عشر، شرح كل من توماس يونغ وفرسنل أوغست بوضوح عملية تداخل وانكسار الضوء ومع العام 1850 تم قبول نماذج الموجة عمومًا.[9] في 1865، تنبؤات جيمس كلرك ماكسويل[10] بأن الضوء عبارة عن موجة كهرومغناطيسية والذي تأكد تقريبًا في 1888 بواسطة تحسس موجات الراديو من قبل هنريك هيرتز'[11]—بدا أنها آخر صيحة لنماذج الضوء الجسيمية.

في 1900، ماكسويل النموذج النظري للضوء على أنه تذبذب مجالين كهربائي ومغناطيسي بدت مكتملة. مع ذلك، العديد من الملاحظات لم يكن ممكنًا تفسيرها بأي نموذج موجي من الإشعاع الكهرومغناطيسي، وهذا أدى للفكرة القائلة بأن طاقة الضوء كانت قد رزمت في كمّات الموصوف بالعلاقة E=hν. بينت تجارب لاحقة أن كمات الضوء هذه تحمل أيضًا كمية تحرك وعليه، يمكن اعتبارها جسيمات: ولد مفهوم الفوتون، مؤديًا إلى تفهم عميق للمجالات الكهربائية والمغنطيسية نفسها.

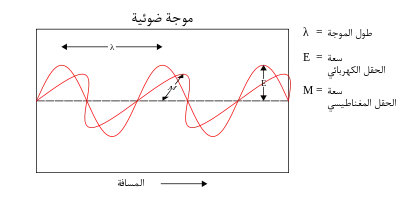
إن نظرية الموجة لماكسويل، مع ذلك، لا تحسب حسابًا لجميع خصائص الضوء. تتنبأ نظرية ماكسويل بأن طاقة موجة الضوء تعتمد فقط على شدتها، ليس على ترددها، على الرغم من أن أنواع عديدة من التجارب المستقلة تظهر أن الطاقة الممنوحة بالضوء للذرات تعتمد على تردد الضوء فقط وليس شدته. على سبيل المثال، بعض التفاعلات الكيميائية يتم إثارتها فقط عن طريق ضوء بتردد أعلى من حد معين. إذا كان هذا الضوء ذا تردد أقل فمهما بلغت شدته لا يحفز التفاعل. بالمثل، بالإمكان نزع الكترونات من صفيحة معدنية بتسليط ضوء ذي تردد عالي بقدر كاف عليها (تأثير كهروضوئي)؛ تتعلق طاقة الالكترونات المنتزعة بتردد الضوء فقط، وليس الشدة.[12][ملاحظات 1]

يتحرك الفوتون في الفراغ بسرعة الضوء 299792458 متر/ثانية وسرعته ثابته لا تتغير إلا إذا دخل وسطًا آخر مثل الزجاج.

وبصفته كمية طاقة تعتمد طاقته ${\displaystyle E}$ على ثابت بلانك ${\displaystyle h}$ وتعطى بالعلاقة:

${\displaystyle E=h\nu \,.}$

حيث:

${\displaystyle \nu }$ تردد موجة الفوتون

ونعطي هنا مثالًا عدديًا لفوتون معهود من الفوتونات الضوئية:

${\displaystyle E=\hbar \omega =(6{,}582\,119\,15\cdot 10^{-16}\ \mathrm {eV\cdot s} )\cdot \omega }$ ,  

حيث:

${\displaystyle E}$ طاقة الفوتون بالإلكترون فولت eV

${\displaystyle \hbar =h/2\pi }$

${\displaystyle \omega }$: التردد الزاوي (1/ثانية).

فإذا كان التردد الزاوي: (في الثانية) ω = 1,520 · 10¹⁵

تكون طاقة الفوتون: E = 1 eV

وهذه طاقة شعاع ضوء في منطقة طيف الأشعة تحت الحمراء.

كما يمكن حساب طاقة الفوتون بمعرفة طول موجته، من المعادلة:

${\displaystyle E=h\cdot \nu =h\cdot c/\lambda =\left(1{,}239\,841\,939\ \mathrm {eV\mu m} \right)/\lambda }$

حيث:

λ طول موجة الفوتون بالميكرومتر

فإذا كانت طول موجة الفوتون تساوي= 1,240 ميكرومتر فهي تساوي 1240 نانومتر

وتكون طاقة الفوتون: E = 1 eV

وللمقارنة فإن شعاع ضوء ذو طول موجة 620 نانومتر يكون لونه برتقالي، وبالتالي تكون طاقته = 2 إلكترون فولت.

والفوتون يتحرك باستمرار بسرعة الضوء ولا يوجد في حالة سكون، لذلك فله كمية حركة ${\displaystyle p}$ وهي تعطى بالعلاقة التالية الناتجة عن ميكانيكا الكم:

${\displaystyle p={\frac {h\nu }{c}}={\frac {h}{\lambda }}\,.}$

ينشأ الفوتون الضوئي في الذرة عندما يقفز أحد إلكترونات الذرة من مستوى طاقة علوي إلى مستوى طاقة سفلي، عندئذ يطلق الإلكترون فارق الطاقة على هيئة فوتونًا له تردد محدد.

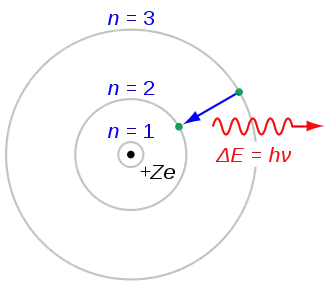
ينشأ الفوتون الضوئي في الغلاف الذري الإلكتروني عندما تتأثر الذرة بفعل الحرارة مثلًا ويصبح أحد الإلكترونات في مستوى طاقة للذرة عال، ولا يستطيع الإلكترون البقاء في ذلك المستوى فسرعان ما يقفز إلى مستوى طاقة سفلي ويطلق فارق الطاقة في هيئة فوتون (شعاع ضوء) له تردد محدد أو ذي طول موجة محددة.

فذرة الصوديوم على سبيل المثال تطلق عند الإثارة شعاعي ضوء تبلغ طول موجتهما 589 نانومتر و 590 نانومتر. ويقع هذان الشعاعان في منطقة اللون الأصفر للطيف، هذان الشعاعان هما فوتونان.

وطيف الزئبق يصدر خطين من الفوتونات طول موجتيهما 579 و 577 نانومتر يقعان في منطقة الضوء الأصفر وخط ثالث ذو طول موجة 546 نانومتر وهذا يقع في منطقة الضوء الأخضر.

وكل من هذه الفوتونات ينشأ عندما يقفز أحد الإلكترونات من مستوى للطاقة عال إلى مستوى منخفض. وتصل طاقة هذه الفوتونات بين 0.5 و 0.6 إلكترون فولت (أي أقل من 1 إلكترون فولت).

وبصفة عامة فالفوتونات عبارة عن أشعة كهرومغناطيسية، بعضها يمكن رؤيته وينتمي إلى أشعة الضوء المرئي، والبعض الآخر يمكن أن يظهر في هيئة شعاع من الأشعة السينية ذات الطاقة العالية وبالتالي فلها درجة نفاذ عالية. وتنشأ الأشعة السينية عندما يقفز إلكترون من مستوى عال في الذرة إلى مكان شاغر في الذرة بالقرب من النواة. فيكون فرق طاقتي المستويين بالغًا ويصل إلى عدة مئات إلكترون فولت.

وهناك نوع من الفوتونات ذو طاقة عالية جدًا تبلغ عدة ملايين إلكترون فولت مثل أشعة غاما. هذه الفوتونات لا تنشأ في الغلاف الذري للعناصر، وإنما تصدر من نواة الذرة.

في عام 1900م كان ماكس بلانك يعمل على مسألة إشعاع الجسم الأسود، وتوصل إلى أن الطاقة في الأمواج الكهرومغناطيسية لا يُمكن أن تنتشر إلا على شكل "حزم صغيرة" من الطاقة، أطلق عليها "الكموم" (جمع كم). لاحقًا وفي عام 1905م ذهب ألبرت آينشتاين إلى أبعد من ذلك حين قال أن الأمواج الكهرومغناطيسية لا يُمكن أن توجد إلا على شكل حزم طاقة.[13] وقد أطلق عليها اسماً مشابهاً وهو "كموم الضوء". أما كلمة "فوتون" فقد اشتقت من الكلمة الإغريقية "φως" (فوس) والتي تعني "ضوء". وقد كان من ابتكر الكلمة هو الفيزيائي غلبرت لويس في عام 1926، والذي نشر نظرية تخمينية -غير تجريبية– حول أن "الفوتونات لا تستحدث ولا تفنى".[14] وبالرغم من أن نظرية لويس لم تلاقِ قبولاً لتعارضها مع العديد من التجارب العلمية، إلا أن معظم الفيزيائيين استخدموا "فوتونه" الجديد مباشرة بعد طرح النظرية. حسب إسحاق أسيموف، آرثر كومبتون هو من عرّف "كموم الطاقة" بأنها "فوتونات" في عام 1923.[15][16]

وعادة ما يُشار في الفيزياء إلى الفوتون برمز "γ" (الحرف الإغريقي "غاما"). وربما استخدم هذا الرمز تيمّناً بأشعة غاما (والتي اكتشفها وأسماها الفيزيائي "باول فيلارد" في عام 1990[17][18]) لأنه تبيّن أنها من الأمواج الكهرومغناطيسية في عام 1914.[19] في الكيمياء والهندسة البصرية يُرمز للفوتونات عادة بالرمز "hν"، حيث أن "h" هو ثابت بلانك و"ν" هو حرف إغريقي يدل على تردد الموجات. ويوجد رمز أقل شيوعاً هو "hf" حيث "f" اختصار للكلمة الإنجليزية "frequency" والتي تعني تردد.

الفوتون عديم الكتلة (انظر أدناه) والشحنة الكهربائية[20] ولا يضمحل في الفضاء الخالي. الفوتون هو البوزون الحامل للقوة الكهرومغناطيسية[21]، ونظريًا كل الأعداد الكمية الأخرى للفوتون (مثل عدد الباريون والأعداد الكمية للنكهة) هي صفر[22]

العلاقة بين طاقة وزخم حركة الفوتون هي "E = pc"، حيث أن "E" هي الطاقة و"p" هي مقدار متجه زخم الحركة و"c" هي سرعة الضوء.[23] طاقة وزخم حركة الفوتون يعتمدان فقط إما على تردده (ν) أو بشكل مساو على طوله الموجي (λ):

${\displaystyle E=\hbar \omega =h\nu ={\frac {hc}{\lambda }}}$

حيث أن "K" هو "متجه الموجة" و"ω" هو التردد الزاوي و"ħ" هو ثابت بلانك.[24]

وأيضًا يملك الفوتون دورانًا مغزليًا لا يعتمد على تردده. ومقدار دورانه هو ${\displaystyle \scriptstyle {{\sqrt {2}}\hbar }}$

تم التحقق من تنبؤات أينشتاين عام 1905 تجريبياً بطرق عدة خلال العقدين الأولين من القرن العشرين. قبل تجربة كومبتون (تأثير كومبتون) التي أثبتت أن الفوتونات حملت زخم حركة متناسب مع رقم الموجة (التردد) كان معظم الفيزيائيين مترددين في الاعتقاد بأن الإشعاع الكهرومغناطيسي قد يكون جسيمي، بدلاً من ذلك كان هناك اعتقاد منتشر بأن تكميم الطاقة ينتج عن بعض القيود الغير معروفة للمادة الماصة والباعثة للإشعاع. تغيرت الآراء بمرور الوقت ويعود التغير بشكل جزئي إلى تجارب مثل تأثير كومبتون، حيث كان من الصعوبة بشدة ألا يعزى التكميم إلى الضوء نفسه لتفسير النتائج الملاحظة.

حتى بعد تأثير كومبتون، قام كل من نيلس بور وهندريك أنتوني كرامرز، وجون كلارك سلاتر بمحاولة أخيرة للحفاظ على نموذج ماكسويل للحقل الكهرومغناطيسي المستمر للضوء والتي أطلق عليها اسم نظرية BKS نسبة إلى (بوهر-كرامرز-سلاتر) (بالإنجليزية: Bohr-Kramers-Slater)‏ ^[en]. لإدخال البيانات التي كانت متوفرة وقتها في الحساب، كان لابد من وضع فرضيتين جذريتين:

1. يتم الحفاظ على الطاقة وزخم الحركة فقط في المرحلة الوسطى للتفاعل بين المادة والإشعاع وليس في العمليات الابتدائية كالامتصاص والانبعاث. هذا يسمح بالتوفيق بين الطاقة المتغيرة المتقطعة للنواة (القفز بين مستويات الطاقة) والتحرير المستمر للطاقة على هيئة اشعاع.
2. التخلي عن السببية: مثال، الإشعاعات التلقائية هي فقط اشعاعات ناجمة عن مجال مغناطيسي "افتراضي".

ومع ذلك، أظهرت تجارب كومبتون المدققة بأن حفظ الطاقة وزخم الحركة يتم بشكل جيد جداً في العمليات الابتدائية، وأن اهتزاز الالكترون وتوليد فوتون جديد في تأثير كومبتون يخضع للسبيبة خلال 10 بيكو ثانية. وفقا لذلك أعطى بور وزملاؤه نهاية مشرفة لنموذجهم قدر المستطاع. ومع ذلك ألهم فشل نموذج نظرية بوهر-كرامرز-سلاتر الفيزيائي فيرنر هايزنبيرغ في تطويره لميكانيكا المصفوفات.

استمر القليل من الفيزيائيين في تطوير النماذج النصف تقليدية والتي تصف الإشعاع الكهرومغناطيسي بأنه غير مكمم وتخضع فيها المادة لقوانين ميكانيكا الكم. بالرغم من أن الأدلة على وجود الفوتونات من التجارب الفيزيائية والكيميائية كانت ساحقة، فإنها لن تؤخذ نتيجة مطلقة، نظراً لاعتمادها على التفاعل بين الضوء والمادة. ومع ذلك دحضت تمامًا كل النظريات النصف تقليدية المعقدة للمادة في السبعينيات والثمانينيات من القرن العشرين بالتجارب المرتبطة بالفوتون. ومنذ ذلك الحين تم الأخذ بعين الاعتبار نظرية أينشتاين بأن التكميم خاصية للضوء نفسه ليتم إثباتها.

• موجة كهرومغناطيسية
• ضوء
• طيف
• طيف كهرومغناطيسي
• ليزر
• تأثير دوبلر
• استقطاب الفوتون
• ميكانيكا الكم
• بوزون قياسي
• حامل قوة
• قوة كهرومغناطيسية
• عودة ارتباط

1. ينبغي فهم أنها "بغض النظر عن كمية الشدة" تشير إلى كميات شدتها تحت 10¹³ W/cm² تقريبا والتي تبدأ عندها نقطة نظرية التشويش بالانهيار. المثير للاهتمام في موضوع الشدة، والذي يكون للضوء المرئي تقريبا فوق 10¹⁴ W/cm²، يتنبأ الوصف الكلاسيكي للموجة أن الطاقة المكتسبة بواسطة الإلكترونات، تدعى طاقة بنديرو الدافعة. انظر أيضًا . بالمقارنة، فإن ضوء الشمس ليس سوى 0.1 W/cm². نسخة محفوظة 11 أكتوبر 2017 على موقع واي باك مشين.
2. أثبتت نظرية النسبية الخاصة لآينشتاين أن كتلة الأجسام يُمكن أن تزيد في حال تحركت بسرعة قريبة من سرعة الضوء. وعند 86% من سرعة الضوء تتضاعف الكتلة. ولذلك فقد وُلد مصطلحان للتعبير عن الكتلة هما: الكتلة السكونية، وهي كتلة الأجسام عندما تكون ثابتة. والكتلة الحركية، وهي كتلة الأجسام عندما تتحرك بما يقارب سرعة الضوء.

في كومنز صور وملفات عن: فوتون

• بوابة الفيزياء
• بوابة بصريات
• بوابة علم المواد