علم الفلك في عصر الحضارة الإسلامية
في تاريخ الفلك، يشير علم الفلك الإسلامي أو علم الفلك العربي إلى الإسهامات الفلكية التي تمت في العالم الإسلامي وخصوصا في العصر الإسلامي الذهبي (القرون 8-15)[1] والتي كتبت غالبا باللغة العربية. وقعت أغلب هذه الإسهامات في الشرق الأوسط وآسيا الوسطى والأندلس وشمال أفريقيا وبعض الأحيان في الشرق الأقصى والهند. نشأ علم الفلك مثله مثل العلوم الإسلامية الأخرى عن طريق استيعاب المواد الأجنبية ودمج العناصر المتباينة لتلك المواد لإيجاد علم يتلائم وخصائص الإسلام. تمثلت هذه المواد الأجنبية في أعمال الساسانيين والهيلينيين والهنود التي ترجمت وجمعت معا.[2] وفي المقابل كان لعلم الفلك الإسلامي تأثير واضح في نظيره البيزانطي[3] والهندي[4] والأوروبي[5] (أنظر الترجمات اللاتينية في أوروبا في القرن الثاني عشر) والصيني[6] والمالي.[7][8]
حتى الآن، احتفظت بعض النجوم في السماء كالدبران والنسر الطائر بأسمائها العربية وكذلك بعض المصطلحات الفلكية كالسمت والعهدة والمقنطرة.[9] عدد كبير من المؤلفات الفلكية الإسلامية بقيت صامدة حتى الآن ويبلغ عددها حوالي 10000 مخطوطة منتشرة حول العالم وكثير منها لم يقرأ أو يصنف ورغم ذلك يمكن تقدير حجم النشاط الإسلامي في علم الفلك.[10]
الإسلام وعلم الفلك
أثر الإسلام في علم الفلك بشكل مباشر وغير مباشر وكان الدافع الرئيسي وراء ازدهار الفلك هو أن ممارسة شعائر الإسلام تتطلب حل مشكلات في علم الفلك الرياضي وخصوصا في الهندسة الكروية.[2]
خلفية
في القرن السابع، كان المسيحيون واليهود يراقبون أطوار القمر من أجل الاحتفال بالأيام المقدسة كالفصح والقيامة. وواجه المجتمعان حقيقة أن الأيام ال29.5 للشهور القمرية لا تتناسب والأيام ال365 للسنة الشمسية. لحل هذا المشكل اتبع المسيحيون واليهود على خطة معتمدة على اكتشاف قام به العالم الفلكي الأثيني ميتون حوالي 430 ق.م. في الدورة الميتونية قسمت التسعة عشر سنة إلى إثنتي عشرة سنة من إثني عشر شهرا قمريا وسبع سنوات من ثلاثة عشر شهرا قمريا. وأبقى الإدراج الدوري للشهور الثلاثة عشر تواريخ التقويم في نفس التاريخ مع المواسم.[2]
من جهة أخرى، استعمل الفلكيون طريقة بطليموس لحساب مكان القمر والنجوم. تعمل طريقة بطليموس على حل المثلثات الفلكية وقسمها مينيلوس من الإسكندرية في القرن الأول. وكانت الطريقة تشمل إنشاء مثلثين قائمين متقاطعين؛ بتطبيق مبرهنة مينلاوس كان من الممكن حل واحد من الأطراف الستة، ولكن فقط إذا كانت الأطراف الخمس الأخرى معروفة. ولمعرفة الوقت انطلاقا من ارتفاع الشمس على سبيل المثال، كان يجب تكرار تطبيق مبرهنة مينلاوس. أما بالنسبة لعلماء الفلك المسلمين في العصور الوسطى، شكل إيجاد طريقة مثلثية بسيطة تحديا واضحا.[2]
النظرة الإسلامية لعلم الفلك
دعى الإسلام المسلم إلى إيجاد طرق لاستعمال النجوم. قال تعالى في سورة الأنعام ﴿وَهُوَ الَّذِي جَعَلَ لَكُمُ النُّجُومَ لِتَهْتَدُواْ بِهَا فِي ظُلُمَاتِ الْبَرِّ وَالْبَحْرِ قَدْ فَصَّلْنَا الآيَاتِ لِقَوْمٍ يَعْلَمُونَ(97)﴾. وعلى أساس هذه الدعوة طور المسلمون أدوات للرصد والإبحار، لذا لا زال العديد من نجوم الإبحار تحمل أسماء عربية.[2]
ومن أهم تأثيرات القرآَن في علم الفلك الإسلامي تأكيده على أن الكون تحكمه مجموعة قوانين وحيدة متأصلة في مفهوم التوحيد الإسلامي ووحدانية الله فضلا عن المكانة الكبيرة للمعطيات التجريبية التي لم تكن شائعة في الحضارة اليونانية السابقة والتي حثت المسلمين على اعتماد منهج الرصد[11] بخلاف الفلاسفة اليونانيين القدامى مثل أفلاطون وأرسطو الذين لم يثقوا في الحواس واعتبروا العقل الوسيلة الوحيدة الكفيلة والناجعة لفهم الطبيعة. حث القرآَن على الملاحظة والرصد والتأمل قادت المسلمين إلى تطوير منهج علمي يتأسس على هذه المفاهيم وأبرزها الملاحظة التجريبية. كتب محمد إقبال قائلا:[12]
تشير عدة أحاديث نبوية على أن نبي الإسلام محمد بن عبد الله كان معارضا للتنجيم والخرافة عامة. وكمثال على ذلك عندما حل الخسوف بعد موت ابنه إبراهيم فبدأت الشائعات تقول بأنه تعزية من الله.:[13]
روي عن ابنِ عمر في صحيح البخاري/1402 وصحيح مسلم/914:
| أَنه كان يخبِر عن النبي صلى الله عليه وسلم : إِن الشمس والقمر لا يخسفانِ لموت أَحد ولا لحياته ولكنهما آيتانِ من آيات اللّه فإِذا رأَيتموها فصلوا. |
ابتداء من القرن الثاني فصاعدا، أصبح الفلكيون المسلمون علماء يعتمدون على الملاحظة عوض عن الفلسفة، وذلك لمعارضة دينية من علماء الفقه من الأشاعرة وأَكبرهم الغزالي الذي عارض استخدام فيزياء وكونيات أَرسطو في علم الفلك، ما يفتح الباب أمام احتمالات لعلم فلك غير مقيد بفلسفة أَرسطو.[14][15] فعلى سبيل المثال أثرت نظرية الأشاعرة على فخر الدين الرازي (1149-1209) فرفض نظرية أَرسطو لمركزية الأَرض في الكون وبدلا من ذلك اقترح متعددا من الأَكوان يشمل عددا لا يحصى من الأَكوان والعوالم، حيث أَن كل عالم من تلك العوالم أَكبر حجما أو كتلة من عالمنا وبه نفس ما يوجد على هذا الأَخير. انتقد الرازي أَيضا النظرة الأَرسطية للفلكات السماوية الصلبة واقترح أَنها مجرد مدار من النجوم. في نفس القرن رفض عضد الدين الإيجي (1281-1355) مبدأَ أَرسطو الفطري لدائرية حركة الأجرام السماوية[16] وأَصر على أَن الفلكات السماوية مجرد أَشياء خيالية وأكثر هشاشة من بيوت العناكب[15] متأَثرا بنظرية العرضية الأشعرية والتي تقول بأن جميع الآثار المادية ناجمة مباشرة عن إرادة الله. وكذلك رفض علي القوشجي (و. 1474) فيزياء أرسطو وعزلها بشكل مطلق عن علم الفلك مما جعل الفلك علما تجريبيا ورياضيا محضا فسمح له ذلك باكتشاف بدائل لفكرة أرسطو عن الأرض القرطاسية، كما أَنه بحث في فكرة أرض متحركة. واستنتج على أساس الأدلة التجريبية بدلا من المضاربة الفلسفية، أن نظرية الأرض المتحركة تماما مثل نظرية الأرض القرطاسية يرجح أن تكون صحيحة وأنه لا يمكن أن نستنتج تجريبيا أي نظرية أصح.[14][15]
القواعد الإسلامية

يلتزم المسلمون بقواعد متعددة لاستعمال مثالي للحسابات والملاحظات الفلكية. أول قاعدة التقويم الهجري حيث قال تعالى في سورة التوبة ﴿إِنَّ عِدَّةَ الشُّهُورِ عِنْدَ اللَّهِ اثْنَا عَشَرَ شَهْرًا فِي كِتَابِ اللَّهِ يَوْمَ خَلَقَ السَّمَاوَاتِ وَالْأَرْضَ مِنْهَا أَرْبَعَةٌ حُرُمٌ ذَلِكَ الدِّينُ الْقَيِّمُ فَلَا تَظْلِمُوا فِيهِنَّ أَنْفُسَكُمْ وَقَاتِلُوا الْمُشْرِكِينَ كَافَّةً كَمَا يُقَاتِلُونَكُمْ كَافَّةً وَاعْلَمُوا أَنَّ اللَّهَ مَعَ الْمُتَّقِينَ(36)﴾.[2][17] لذا لم يتبع المسلمون التقويم المسيحي أو العبري وكان عليهم تطوير واحد خاص بهم.
أما القاعدة الثانية هي أن الشهور الإسلامية لا تبدأ مع المحاق الفلكي وهو الوقت الذي يكون للقمر والشمس نفس خط الطول السماوي وبذلك يكون غير مرئي وبدلا من ذلك تبدأ حين يرى الهلال أول مرة في سماء المساء الغربية.[2] وقال تعالى في سورة البقرة ﴿يَسْأَلُونَكَ عَنِ الأهِلَّةِ قُلْ هِيَ مَوَاقِيتُ لِلنَّاسِ وَالْحَجِّ وَلَيْسَ الْبِرُّ بِأَنْ تَأْتُوْاْ الْبُيُوتَ مِن ظُهُورِهَا وَلَـكِنَّ الْبِرَّ مَنِ اتَّقَى وَأْتُواْ الْبُيُوتَ مِنْ أَبْوَابِهَا وَاتَّقُواْ اللّهَ لَعَلَّكُمْ تُفْلِحُونَ(189)﴾.[18][19] هذا ما قاد المسلمين لرصد أدوار القمر في السماء وأدت جهودهم إِلى حسابات رياضية جديدة وأدوات رصد جديدة فضلا عن تخصيص علم لرؤية القمر.[20]
وأيضا واجب على المسلمين الصلاة في اتجاه الكعبة بمكة وتوجيه مساجدهم نحوها لذا فمن المفروض تحديد اتجاه مكة من أي مكان كان.[21][22] هناك عامل مؤثر آخر هو مواقيت الصلاة فيجب معرفة الأجرام السمواية بدقة واستنتاج مواعيد الصلاة منها في وقت الشروق والزوال والعصر والغروب والمساء.[2][23]
ضرورة الهندسة الكروية
 طالع أيضًا: الرياضيات عند المسلمين
طالع أيضًا: الرياضيات عند المسلمين
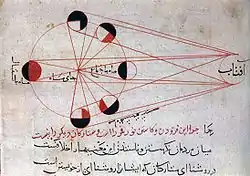
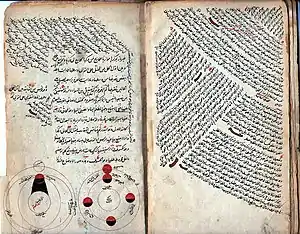
شكل توقع وقت ظهور الهلال تحديا للفلكيين الرياضيين المسلمين. رغم أن نظرية بطليموس لحركة القمر المعقدة كانت تحدد وقت القمر الجديد، إلا أنها تحدد مسار القمر بعلاقته مع مسير الشمس ولتوقع أول ظهور للقمر كان من الواجب وصف حركته وعلاقتها بالأفق وهذا المشكل تطلب هندسة كروية متطورة.[24] كانت معرفة وقت الصلاة واتجاه مكة السببين الرئيسيين وراء إسهامات المسلمين في الهندسة الكروية. حل هاتين المشكلتين تطلب إيجاد الأضلاع أو الزوايا الغير معروفة في مثلث في فلكة سماوية انطلاقا من المعروف من الأضلاع والزوايا. وكمثال على ذلك لمعرفة الوقت في اليوم، وجب إنشاء مثلث تشكل رؤوسه سمت الرأس والقطب السماوي الشمالي وموضع الشمس. يجب على الملاحظ معرفة دائرة عرض الشمس ودائرة عرض القطب الأولى يمكن ملاحظتها والثانية مساوية لخط عرض الملاحظ. الوقت نستنتج في الآخر من الزاوية بين خط الزوال (القوس بين سمت الرأس والقطب) ودائرة ساعة الشمس (القوس بين الشمس والقطب).[2][23]
تفسيرات كونية
هناك عدة آيات قرآنية (610-632) يفسرها بعض الكتاب الوسيطيين والمعاصرين على أنها تنذر بالنظريات الكونية الحديثة.[25] ومن أقدم الأمثلة على ذلك نجده في أعمال الفقيه فخر الدين الرازي (1149-1209) في تصوره للفيزياء والعالم المادي في كتاب المطالب فناقش علم الكون الإسلامي وانتقد مركزية الأرض في الكون واستكشف مفهوم تعدد الأكوان كما فعل معاصروه انطلاقا من القرآن (الحمد لله رب العالمين). وتسائل حول ماذا تعني كلمة (العالمين)، عدة عوالم في كون أو كوسمو وحيد أم متعددا من الأكوان مختلين عن الكون المعروف. ورفض النظرة الأرسطية للكون الوحيد لصالح وجود عدة أكوان وعوالم وآمن بنظرته التي يؤيدها القرآن ونظرية الذرية للأشاعرة.
اليوم، تفسر هاته الآيات على أنها تـُعلم بتوسع الكون وحتى بنظرية الانفجار العظيم:[26]
قال تعالى في سورة البقرة ﴿وَإِذْ قَالَ رَبُّكَ لِلْمَلاَئِكَةِ إِنِّي جَاعِلٌ فِي الأَرْضِ خَلِيفَةً قَالُواْ أَتَجْعَلُ فِيهَا مَن يُفْسِدُ فِيهَا وَيَسْفِكُ الدِّمَاء وَنَحْنُ نُسَبِّحُ بِحَمْدِكَ وَنُقَدِّسُ لَكَ قَالَ إِنِّي أَعْلَمُ مَا لاَ تَعْلَمُونَ(30)﴾[27]
قال تعالى في سورة الذاريات ﴿وَالسَّمَاءَ بَنَيْنَاهَا بِأَيْدٍ وَإِنَّا لَمُوسِعُونَ(47)﴾[28]
والبعض يفسر هذه الآية كإعلام مسبق بمفهوم شكل الأرض الإهليلجي المعاصر:[25]
قال تعالى في سورة النازعات ﴿وَالْأَرْضَ بَعْدَ ذَلِكَ دَحَاهَا(30)﴾[29]
هذا تفسير على أن الآية تنطوي ضمنا على الشكل الإهليلجي للأرض لكامل بن سالم:
لذا ترجم رشاد خليفة الآية كما يلي:
التاريخ
كانت معرفة العرب قبل الإسلام للنجوم استنباطية وتقتصر على ما يلاحظونه من ظهورها أو اختفائها. وكان بزوغ الإسلام السبب وراء تقدم العرب في ميدان الفلك.[31] بدأ علم الفلك الإسلامي بنفس طريقة بداية العلوم الإسلامية الأخرى وذلك بجمع المواد الأجنبية ودمج العناصر المتباينة لتلك المواد لخلق علم يقوم أساسا على الإسلام. تضمنت هذه المواد أعمال الساسانيين والهيلينيين والهنود التي ترجمت وجمعت معا.
قسم مؤرخ العلوم دونالد روتلدج هيل تاريخ الفلك الإسلامي إلى أربعة حقب مختلفة:[31]
- الجمع والتوفيق بين علم الفلك الهندي والساساني والهيليني (700—825 ب.م)
- التحقق في نظام بطليموس وقبوله وتعديله (825—1025 ب.م)
- ازدهار النظام الإسلامي المميز لعلم الفلك (1025—1450 ب.م)
- عصر الركود حيث ظهرت مساهمات قليلة (1450—1900 ب.م)
610-700
منذ البداية، لاحظ مسلمو المدينة القمر الجديد لمعرفة بداية الشهور وخصوصا رمضان والأيام المقدسة. في حوالي 638 ب.م، اتبع الخليفة عمر تقويما قمريا جديدا يقوم على النظرة الإسلامية. احتوى هذا التقويم على إثني عشر شهرا وتبدأ هذه الشهور عند رؤية الهلال وكان أصغر من التقويم الشمسي بحوالي أحد عشر يوم. لا زال هذا التقويم مستعملا إلى يومنا هذا وذلك لأغراض دينية.[2][32]
700-825
كانت هذه الفترة فترة جمع وموافقة للإسهامات الهيلينية والهندية والساسانية.
الدوافع
يرى المؤرخون أن عدة عوامل ساهمت في ازدهار علم الفلك الإسلامي كان أولها قرب العالم الإسلامي المعرفة القديم حيث ترجم الكثير من الكتابات اليونانية والسنسكريتية والفارسية إلى اللغة العربية خلال القرن التاسع وتعززت هذه العملية بفعل تسامح علماء الدين مع الديانات الأخرى.[2]
كان الدافع الثاني يتمثل في المراقبات الدينية الإسلامية والتي زادت من المشاكل الفلكية الرياضية. وعند حل هذه المشكلات الدينية تفوت العلماء المسلمون على الأساليب الرياضية اليونانية.[2]
التأثيرات القديمة وحركة الترجمة
خلال هذه الفترة، ترجمت بعض الأعمال السنسكريتية والفارسية الوسيطية إلى اللغة العربية. كان أبرز هذه الأعمال زيج السندهند[33] المقتبس من سوريا سندهاتا وأعمال براهماغوبتا التي ترجمها محمد الفزاري ويعقوب بن طارق في 777. تشير المصادر إلى أن الترجمات حدثت بعد زيارة فلكي هندي إلى قصر الخليفة المنصور في 770. كان أبرز عمل مترجم من الفارسية الوسيطية زيج الشاه وهو مجموعة من الجداول الفلكية التي جمعت في بلاد فارس الساسانية على مدى قرنين.
تشير كتابات من ذلك الوقت إلى أن العرب اعتمدوا دالة الجيب (الموروثة من علم المثلثات الهندي) بدلا من أوتار القوس المستخدمة في الرياضيات الهيلينية.[31] ومن التأثيرات الهندية صيغة تقريبية استخدمها علماء الفلك المسلمون لضبط الوقت.[34]
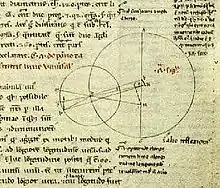
كان اهتمام الإسلام بالفلك موزايا لاهتمامه بالرياضيات ويعتبر المجسطي خير مثال على ذلك (ك. 150) للفلكي بطليموس (100-178). كان المجسطي معلما في مجال الفلك جامعا، كما يجمع العناصر لإقليدس أعمال الهندسة، لكل المعرفة في علم الفلك التي كانت لمؤلفه. كان هذا الكتاب معروفا في الأول باسم الأطروحة الرياضية وبعد استعماله عرف باسم عالم الفلك العظيم. عرف في العالم الإسلامي باسم المجسطي المؤخوذ من الاسم اليوناني مجيسط (باليونانية: megiste) (وتعني العظيم) بزيادة ال للتعريف وعند الغرب باسم Almagest بسبب الاستعمال الشائع في الترجمات.[35] رغم أن معظم الكتاب أخطاء ظل يستعمل في أوروبا والعالم الإسلام كمرجع فلكي مهم حتى نهضة مراغة ونهضة كوبرنيكوس.[36] ألف بطليموس أعمالا أخرى كالبصريات وهارمونيكا ويقترح البعض أنه هو من كتب تترابيبلون.
كان المجسطي عملا جامعا لقوائمه الشاملة للظواهر الفلكية وشمل الكتاب جداول زمنية لملوك آشور والأخمينيين والإغريق والرومان لاستخدامها في حساب انقضاءالزمن بين الأحداث الفلكية المعروفة والتواريخ الثابتة. وبالإضافة إلى أهميته بالنسبة لحساب التقاويم بدقة ربط المجسطي الثقافات الأجنبية والمتباعدة معا بمصلحة مشتركة في النجوم والتنجيم. قـُرأ عمل بطليوس مرارا وتكرارا ودـُقق على أيادي علماء الفلك والمنجمين العرب والفرس والمسلمين الآخرين.
825-1025
شكلت الفترة من القرن التاسع إلى أوائل القرن الحادي عشر فترة تحقق وتدقيق لتفوق نظام بطليموس للفلك وفترة للإسهامات الهامة فيه. دعم الخليفة العباسي المأمون البحث الفلكي وأصبحت بغداد ودمشق عاصمتين للفلك. لم يكن الخلفاء داعمين ماليين لعلم الفلك فقط بل أعطوا لهذا العلم قيمة وأهمية كبيرة.[37] وقد بني في عهده مرصدان فلكيَّان: مرصد الشماسية في بغداد، ومرصد جبل قاسيون في دمشق.
بداية الفلك الرصدي

في الفلك الرصدي، كان أول كتاب مهم لدى العلماء المسلمين هو زيج السند للخوارزمي في 830. احتوى الكتاب على جداول حركة الشمس والقمر والكواكب الخمسة المعروفة في ذلك الوقت وظهرت أهميته في أنه أدخل المفاهيم الهندية ومفاهيم بطليموس في العلوم الإسلامية. مثل هذا العمل أيضا نقطة تحول في علم الفلك الإسلامي. حتى ذلك الوقت، كان الفلكيون المسلمون يعتمدون نهج البحث الأولي في الحقل وترجمة أعمال الآخرين وتعلم المعرفة المكتشفة من قبل. تميز عمل الخوارزمي بكونه بداية أساليب غير تقليدية للدراسة والحسابات.[38]
بين العامين 825 و 835، أجرى أحمد بن عبد الله المروزي عدة ملاحظات في مرصد الشميسية ببغداد حيث قدر عددا من القيم الجغرافية والفلكية[39] وجمع نتائجه في كتاب الأبعاد والأجرام الذي اقترب بتقديراته إلى الأبعاد الحالية أكثر ممن سبقوه. فعلى سبيل المثال، قدر قطر القمر ب3037 كلم (تساوي 1,519 كلم بنصف القطر) وبعده عن الأرض ب 215209 ميل وهذه النتائج تقارب المسافات الحالية (1735 نصف قطر و 238857 ميل).[40]
في 850، ألف أحمد بن كثير الفرغاني جوامع علم النجوم والحركات السماوية الذي قدم فيه موجزا عن علم الكون البطليموسي وصحح المجسطي لبطليموس استنادا إلى نتائج توصل إليها علماء الفلك الفرس سابقا. أعطى الفرغاني قيما مراجعة لالتواء مسير الشمس والحركة البدارية لقبا الشمس والقمر ومحيط الأرض. تداول الناس هذه الكتب في العالم الإسلامي وترجمت إلى اللاتينية.[41]
ألف محمد بن جابر بن سنان البتاني (853-929) جداول مطورة لمدارات الشمس والقمر احتوت على اكتشافه الكبير بأن منحى شذوذ مدار الشمس كما سجله بطليموس متغير.[42] من بين أمور أخرى قام بها، عمل على حساب وقت أول ظهور للهلال بعد القمر الجديد وقياس طول السنة الشمسية والسنة الفلكية وتوقع الخسوف والتزيح.[43] في نفس الوقت، قام يحيى بن أبي المنصور بملاحظات وتجارب واسعة وكتب الزيج الممتهن حيث راجع فيه أبعاد المجسطي.[44]

في القرن العاشر، قام عبد الرحمن بن عمر الصوفي برصد النجوم وأعطى وصفا لمواقعها ومقاديرها ودرجة سطوعها وألونها ورسومها في كوكباتها في كتابه صور الكواكب الثمانية والأربعين (964). قدم أيضا أول وصف ورسم لسحابة صغيرة تعرف اليوم باسم مجرة المرأة المسلسلة حيث ذكر أنها رابطة أمام فم السمكة الكبيرة وهي اسم كوكبة عربية. كانت هذه السحابة معروفة لدى فلكيي أصفهان من قبل في حوالي 905 ب.م.[45] وذكر أيضا عبد الرحمن لأول مرة سحابة ماجلان الكبرى.[46][47]
رصد ابن يونس أكثر من 10000 مدخل لمواقع الشمس لعدة أعوام مستعملا أسطرلابا كبيرا بلغ قطره حوالي 1.4 متر. بقيت ملاحظاته لخسوف القمر مستعملة لقرون حتى عندما تحرى سيمون نيوكومب عن حركة القمر أما ملاحظاته الأخرى فألهمت بيير لابلاس في نظريتي إعوجاج مسير الشمس وعدم المساواة بين المشتري وزحل.[48] حسب الخجندي بدقة الميل المحوري ووجد أنه يساوي 23°32'19" (23.53°).[49]
في 1006 رصد الفلكي المصري علي بن رضوان س ن 1006 أكثر المستعرات العظمى الملاحظة سطوعا في التاريخ وترك وصفا مفصلا للنجم المؤقت حيث قال أن الجسم أكبر بحوالي ضعفين إلى ثلاثة أضعاف من قرص الزهرة وله ربع سطوع القمر وأنه منخفض في الأفق الجنوبي. أيد رهبان دير البنيديكتين في سانت غال ملاحظات علي بن رضوان وتوافقوا معه في الحجم والموقع في السماء.
النماذج شمسية المركز الأولى
طور الفلكي البابلي، سلوقس السلوقي نظرية مركزية الشمس لأرسطرخس الساموسي في القرن الثاني ق.م وكتب كتاب ترجم إلى العربية. لم يتبق من الكتاب غير صفحة مترجمة إلى العربية ذكرها الفيلسوف الفارسي أبو بكر الرازي (865-925).[50] في أواخر القرن التاسع أنجز أبو معشر جعفر بن محمد بن عمر البلخي نظاما للكواكب قد فسره البعض كنظام شمسي المركز. ويرجع ذلك إلى ثورته على نظرية مركزية الأرض لصالح نظرية الكواكب المدارية وهي النظرية الوحيدة التي تذكر نظرية مركزية الشمس. لم يصمد عمله حول نظرية الكواكب لكن حفظت البيانات الفلكية التي توصل إليها في أعمال الهاشمي والبيروني والسجزي.[51]
في بداية القرن الحادي عشر، التقى أبو الريحان البيروني عدة علماء هنود آمنوا بنظرية مركزية الشمس. ناقش البيروني نظريات دوران الأرض التي دعمها براهماغوبتا وفلكيون هنود كثر في تحقيق ما للهند من مقولة مقبولة في العقل أو مرذولة وفي القانون المسعودي كتب أن أتباع أريابهاتا عينوا أول حركة من الشرق إلى الغرب نحو الأرض، والحركة الثانية من الغرب إلى الشرق نحو النجوم الثابتة.
كتب البيروني أيضا أن السجزي اعتقد أن الأرض تتحرك واخترع أسطرلابا مبنيا على هذه الفكرة سماه الزورقي:[52]
في كتابه تحقيق ما للهند من مقولة مقبولة في العقل أو مرذولة يشير البيروني إلى عمله في تفنيذ نظرية مركزية الشمس، مفتاح علم الهيئة، والذي هو الآن مفقود:[52]
علم الكونيات
بخلاف الفلاسفة اليونان الذين اعتقدوا أن الكون موجود منذ الأبد، طور الإلاهيون والفلاسفة الوسيطيون مفهوم يقر ببداية للكون وبذلك له ماض نهائي (انظر نهائية مؤقتة). كان هذا المفهوم قائما على نظرية الخلق التي تتحد فيها الديانات الإبراهيمية: اليهودية والمسيحية والإسلام. كان الفيلسوف المسيحي جون فيلوبونوس أول من قدم حجة ضد مفهوم أبدية ماض الكون اليوناني واعتمدت حججه من قبل العديد من الفلاسفة وأبرزهم الفيلسوف المسلم الكندي والفيلسوف اليهودي سعيد بن يوسف والفقيه الغزالي. استعمل هؤلاء حجتين فقهيتين ضد الماضي الأبدي أولاهما استحالة وجود فعلي لانهائي والتي تنص على:[53]
- "لا يمكن لوجود لانهائي فعلي الوجود."
- "التراجع اللانهائي الزمني للأحداث هو وجود فعلي لانهائي."
- ".•.لا يمكن لتراجع لانهائي زمني الوجود."
وثاني الحجتين هي استحالة إتمام وجود فعلي لانهائي بزيادة متعاقبة وتنص على:[53]
- "لا يمكن إتمام وجود فعلي لانهائي بزيادة متعاقبة."
- "أتممت سلسلة الأحداث الزمنية الماضية بزيادة المتعاقبة."
- ".•.لا يمكن لسلسلة الأحداث الزمنية الماضية أن تكون وجودا فعليا لانهائيا."
اعتمدت كلتا الحجتين من قبل الفلاسفة وعلماء اللاهوت المسيحيين وأصبحت الحجة الثانية أكثر شهرة بعد أن اعتمدها إيمانويل كانت في أطروحته للتناقض الأول حول الزمن.[53]
علم الكونيات الفيزيائية وعلم الفلك الحركي والملاحظات الفلكية

في القرن التاسع، قام الأخ الأكبر من بني موسى وهو أبو جعفر محمد بن موسى بن شاكر بإسهامات مهمة في الفيزياء الفلكية والميكانيكا السماوية وكان أول من اقترح أن الأجرام والفلكات السماوية تخضع لنفس القوانين الفيزيائية التي تخضع لها الأرض عكس المعتقد السائد في ذلك الوقت بأن الفلكات السماوية لها قوانينها الخاصة المتحكمة فيها.[54] في القرن العاشر، استحدث محمد بن جابر بن سنان البتاني (853-929) فكرة تجريب الملاحظات السابقة بطرق جديدة.[55] أدى ذلك إلى استخدام علماء الفلك المسلمين الملاحظات والتقنيات التجريبية بكثرة ابتداء من القرن الحادي عشر.[56]
في أوائل القرن الحادي عشر، كتب ابن الهيثم مقالة في ضوء القمر قبل 1021 التي كانت أول محاولة ناجحة في الجمع بين علم الفلك الرياضي والفيزياء وأول محاولة لتطبيق أسلوب المنهج التجريبي في علم الفلك والفيزياء الفلكية. دحض الرأي المعترف به عالميا أن القمر يعكس ضوء الشمس مثل المرآة، وخلص إلى أن الضوء ينبعث من أجزاء سطح القمر التي يصلها ضوء الشمس ولإثبات رأيه أن الضوء ينبعث من كل نقطة من سطح القمر المضاء بنى جهازا تجريبيا عبقريا. صاغ ابن الهيثم مفهوما واضحا للعلاقة بين النموذج المثالي الرياضي والظواهر الملاحظة المعقدة وخصوصا كان أول من قام باستخدام منهجي لتغيير الظروف التجريبية بطريقة ثابتة وموحدة في تجربة تبين أن شدة بقعة ضوء تشكلت عن القمراء تمر من بؤرتين على شاشة تقل باستمرار كلما أغلقنا إحدى البؤرتين.[57]
كان ابن الهيثم أيضا أول من اكتشف أن الفلكات السماوية لا تتكون من مادة صلبة وأن السماوات أقل كثافة من الهواء وذلك في كتابه المناظر (1021). كرر ويتيلو نفس آراء ابن الهيثم وكان لها تأثير كبير على منظومتي كوبرنيكوس وتيخو للفلك.[58]
فند ابن الهيثم نظرة أرسطو لمجرة درب التبانة الذي اعتقد أن المجرة نتجت عن اشتعال زفير بعض النجوم التي كانت كبيرة ومتعددة وقريبة من بعضها البعض وأن الاشتعال يحدث في الجزء العلوي من الغلاف الجوي، في المنطقة التي الحركات السماوية مستمرة بها.[59] وقد اعتمد في ذلك على أول محاولة لرصد وقياس تخاطل درب التبانة[60] وبالتالي حدد ذلك لأنه لم يكن لدرب التبانة تخاطل، وكانت بعيدة جدا عن الأرض ولا تنتمي إلى الغلاف الجوي.[61]
في القرن الحادي عشر أيضا، استحدث أبو الريحان البيروني المنهج التجريبي في علم الفلك وكان أول من قاد أبحاثا تجريبية متعلقة بظواهر فلكية.[62] اكتشف البيروني أيضا أن مجرة درب التبانة هي عبارة عن مجموعة من النجوم السديمة.[63] في أفغانستان، رصد ووصف كسوف الشمس في 8 أبريل 1019 وخسوف القمر في سبتمبر 1019 بالتفصيل وأعطى دائرة عرض النجوم خلال الخسوف.[62]
1025-1450
خلال هذه الفترة، بزغ نظام إسلامي خاص في علم الفلك. كان الفصل بين الرياضيات الفلكية (كما صاغها بطليموس) وفلسفة الكون (كما صاغها أرسطو) عادة موروثة عن اليونان. طور العلماء المسلمون نظاما يسعى لمعرفة التكوين الحقيقي المادي للكون (علم الهيئة) ويجمع بين مبادئ الرياضيات والفيزياء. في إطار علم الهيئة، تسائل الفلكيون المسلمون حول التفاصيل التقنية لنظام بطليموس للفلك.[64] جل هذه الانتقادات تابعت بارادايم بطليموس الفلكي وبقيت في إطار نظرية مركزية الأرض[65] وكما قال مؤرخ الفلك عبد الحميد صبرا:
رغم ذلك ناقش بعض الفلكيين المسلمين، كأبي الريحان البيروني ونصير الدين الطوسي، إذا كانت الأرض تتحرك وتأثير ذلك على الحسابات الفلكية والنظم الفيزيائية القائمة.[67] أما من ناحية أخرى طور علماء مدرسة مراغة للفلك نماذج لكواكب تتعارض والنماذج البطليموسية في إطار نظرية مركزية الأرض اعتمدها كوبرنيكوس في إطار نظرية مركزية الشمس.
تفنيد التنجيم
فند عدة علماء مسلمين التنجيم منهم أبو نصر محمد الفارابي وابن الهيثم وابن سينا وأبو الريحان البيروني وابن رشد. وتنوعت أسبابهم في هذا التفنيد منها العلمية (كانت أساليب المنجمين حدسية وغير استنباطية) والدينية (صدام المنجمين مع علماء الدين).[68]
استعمل ابن قيم الجوزية (1292-1350)، في كتابه مفتاح دار السعادة، حججا استنباطية في علم الفلك لدحض ممارسات التنجيم والتنبؤ.[69] اعترف أن النجوم أكبر من الكواكب وأن عطارد هو أصغر كوكب عرفه في ذلك الوقت قائلا:[70]
اعترف الجوزية أيضا أن مجرة درب التبانة هي عبارة عن أجرام كوكبية صغيرة جدا مرتكزة في فلك الثوابت واستنتج بالتالي أن معرفة جميع المؤثرات الفلكية غير ممكن.[70]
الفيزياء الفلكية والميكانيكا السماوية
في الفيزياء الفلكية والميكانيكا السماوية، وصف أبو الريحان البيروني جاذبية الأرض:
اكتشف البيروني أيضا أن التجاذب يحدث بين الأجرام والفلكات السماوية، وانتقد نظرة أرسطو إلى الأجرام بأنها لا تملك خفة أو جاذبية وحول الحركة الدوارنية بأنها خاصية فطرية للأجرام السماوية.[72]
في 1121، قال عبد الرحمن الخازني في أطروحته كتاب ميزان الحكمة:[73]
إذا كان الخازني أول من يقترح أن نظرية الجاذبية أو طاقة الوضع الثقالية لجسم تتغير حسب مسافته عن مركز الأرض. لم يتم اثبات هذه الظاهرة حتى القرن الثامن عشر بعد قانون الجذب العام لنيوتن.[73]
أيضا في القرن الثاني عشر، شارك فخر الدين الرازي في مناظرة بين العلماء المسلمين حول اعتبار الفـِلكات السماوية أو المدارات (الفـَلك) إما حقيقية أي هيئات مادية أو مجرد دوائر في السماوات تبقى بعد مرور النجوم والكواكب عاما في الداخل وعاما في الخارج. أشار الرازي أن عدة فلكيين مسلمين اتفقوا على أنها فلكات صلبة حيث تدور النجوم بينما آخرون مثل الضحاك آثروا على اعتبارها مدارات رسمتها النجوم وليست أجساما. أما الرازي فلم يكن متيقنا من أي الرأيين يتبع الفلكات السماوية المجردة أو الملموسة وأكد على ضرورة توافقها مع الحقيقة الخارجية وأضاف أنه لا يمكن التأكد من خصائص السماوات بالديل الملاحظ أو دلائل القرآن والسنة النبوية. استنتج أن النماذج الفلكية لا تستند، بفائدتها أو سلبيتها لتنظيم السماوات، على براهين عقلانية سليمة وهكذا لا يمكن القيام بأي التزام فكري عليها بقدر ما كان وصف وشرح الحقائق السماوية هو المعني.
بداية علم الهيئة
ما بين عامي 1025 و 1028، استحدث ابن الهيثم علم الهيئة وهو فرع من علم الفلك في كتابه الشكوك على بطليموس. كان علم الهيئة يبحث في استيعاب الفرضيات الرياضية على هيئة أجرام وفلكات سماوية كل جرم على حدى حول محوره -بعبارة أخرى- إيجاد وصف فيزيائي معقول حول ما يحدث في السماء.[74] كان ابن الهيثم أول من انتقد نظام بطليموس الفلكي معتمدا على أسس رصدية واستنباطية وتجريبية[75] وأول من اقترح ربط حركات مادية حقيقية بنقط ودوائر ومستقيمات رياضية وهمية مع الإبقاء على الحقيقة المادية لمركزية الأرض:
طور ابن الهيثم بنية فيزيائية لنظام بطليموس في أعمال له مثل مقالة في تكوين الكون أو مقالة في هيئة العالم والذي أصبح عملا مهما في علم الهيئة.[76] وفي خلاصة الفلك، أكد على أن الأجرام السماوية تقبل القوانين العلمية.[77]
النماذج البديلة الأولى
في 1030، ناقش أبو الريحان البيروني نظريات الكواكب الهندية لأريابهاتا وبراهماغوبتا وفاراهامهرا في كتابه تاريخ الهند. صرح البيروني أن براهماغوبتا وعلماء آخرون يعتبرون أن الأرض تدور حول نفسها وأضاف أن ذلك لا يشكل أي مشاكل رياضية.[78]
اقترح أبو سعيد السجزي، وهو عالم عاصر البيروني، حركة دوران الأرض حول الشمس كمركز لمدارها ولم يرفض البيروني ذلك.[79] وافق البيروني على دوران الأرض حول محورها ورغم بقاءه في حياد بين نظريتي مركزية الشمس أو مركزية الأرض[80]، اعتبر الأولى مشكلة فلسفية.[5] ولاحظ البيروني أنه إذا كانت الأرض تدور حول نفسها وحول الشمس فإن ذلك لن يغير شيئا من معلماته الفلكية لأنه لن يغير دوران الأرض حول نفسها شيئا من الحسابات والمعرفة الفلكية فهي صحيحة طبقا للنظرية الأولى أو الثانية ومن هنا رأى أن حل هذه المسالة صعب.[81]
في 1031، أنهى البيروني موسوعته الفلكية الموسعة كتاب القانون المسعودي[82]، حيث أورد فيه نتائجه وجداوله الفلكية وتمثيلا أرضي المركز وبوب مسافات الفلكات السماوية عن الأرض المركزية والتي حسبها بالاعتماد على مبادئ المجسطي لبطليموس.[83] قدم الكتاب الأساليب الرياضية لتحليل تسارع الكواكب وصرح فيه أن ذروة الشمس ليست البدارية. اكتشف البيروني أيضا أن المسافة بين الأرض والشمس أكبر من تقديرات بطليموس على أساس أنه تجاهل الكسوفات الحلقية.
في 1070، طرح أبو عبيد الجوزجاني، تلميذ ابن سينا، تعديلا مغايرا لنظريات بطليموس في كتابه طريق الأفلاك. أشار الجوزاني في عمله إلى إشكال الإكوانت في نظام بطليموس وتوصل إلى حل له. وادعى أيضا أن أستاذه ابن سينا توصل إلى حل إشكال الإكوانت.[84]
الثورة الأندلسية

في القرنين الحادي عشر والثاني عشر، ألف فلكيو الأندلس مثل مسلمة المجريطي وابن الصفار أعمالا عدة واستخدموا آلات كثيرة. وعرف لاحقا عن أمية بن عبد العزيز بن أبي الصلت أنه من نقل الكتب الفلكية الأندلسية الأولى إلى شمال أفريقيا حيث بقيت صامدة. انخرط تلامذتهم في التحدي الذي رفعه ابن الهيثم سابقا لتطوير بعيد عن قوانين بطليموس لتصحيح أخطاء التمثيلات مركزية الأرض.[85] احتوى الكتاب الأندلسي المجهول مؤلفه الاستدراك على بطليموس كنقد ابن الهيثم على لائحة لاعتراضات على علم الفلك البطليموسي. كان هذا بداية لثورة المدرسة الأندلسية على مبادئ بطليموس والتي سميت في بعض الأحيان الثورة الأندلسية.[86]
في القرن الثاني عشر، رفض الفيلسوف ابن رشد وعالم الفلك أبو اسحق البطروجي، متأثرين بأفكار ابن طفيل، أفلاك التدوير وتباين المراكز التي استحدثها بطليموس. اعتبرا أن نظام بطليموس غير متسق مع مبادئ أرسطو الفيزيائية واقترح نظاما متراكزا للكون. فشل البطروجي في محاولته تقديم نموذج دقيق لحركة الكواكب مستعملا الفلكات المتراكزة[87] وكتب ابن رشد انتقادا لنظام بطليموس لحركة الكواكب قائلا أن تأكيد وجود فلكة تدويرية أو فلكة متباينة المركز مخالف للطبيعة وأن علم الفلك في عصرنهم ذاك لا يقدم الحقيقة ولكن يتسق فقط مع حسابات وليس مع ما هو موجود حقيقة.[2]

اقترح ابن باجة أن مجرة درب التبانة مكونة من عدة نجوم لكنها تظهر صورة واحدة بسبب الانكسار الحاصل في الغلاف الجوية وذكر رصده لاقتران المشتري والمريخ في 500 هجرية (1106-1107).[59]
في طليطلة، كتب الفلكي المولدي إبراهيم بن يحيى الزرقالي (1029-1087) متعمقا في الأزياج الطليطلية. وحفظ ابن الكماد عمله وأكده ابن هيم الإشبيلي.
مدرسة مراغة
كانت مدرسة مراغة تقليدا فلكيا ظهر في مرصد مراغة وامتد إلى جامع دمشق ومرصد سمرقند. حاول فلكيو مراغة، كما فعل الذين سبقوهم في الأندلس، حل الإكوانت وإيجاد بدائل لنظام بطليموس. حقق فلكيو مراغة نجاحا أكثر من نظرائهم في الأندلس حيث أوجدوا بدائل للنظرية تلغي الإكوانت والتباين المركزي وكانوا أكثر دقة من نظام بطليموس في توقع مواضع الكواكب حسابيا وأفضل اتساقا مع الملاحظات الاستنباطية.[88] من أبرز هؤلاء العلماء نجد محيي الدين الأوردي (م 1266) ونصير الدين الطوسي (1201-1274) ونجم الدين القزويني الكاتبي (م 1277) وقطب الدين الشيرازي (1236-1311) وصدر الشريعة البخاري (و 1347) وابن الشاطر (1304-1375) وعلي القوشجي (و 1447) وعبد العالي البيجرندي (و 1525) وشمس الدين الخافري (و 1550).[89]
وصف بعض المؤرخين أعمال فلكيي مراغة في القرنين الثالث عشر والرابع عشر بثورة مراغة أو ثورة مدرسة مراغة أو الثورة العلمية قبل عصر النهضة. من أهم أوجه هذه الثورة هو إدراك قدرة علم الفلك على وصف الأجسام الفيزيائية بلغة رياضية ووجوب عدم بقاء علم الفلك فرضيات رياضية لأن ذلك يوثق الظاهرة فحسب. أدرك فلكيو مراغة أن نظرة أرسطو للحركة بوصفها إما خطية أو دورانية غير صحيحة كما أظهرت مزدوجة الطوسي أن الحركة الخطية يمكن إنتاجها بحركات دورانية.[90]
على عكس الفلكيين الإغريق والهيلينيين، الذين لم يعنوا بالتوفيق بين مبادئ الفيزياء ومبادئ الرياضيات لنظرية الكواكب، أصر الفلكيون المسلمون على جمع الرياضيات بالعالم الحقيقي المحيط بهم[91] والتي تحولت من حقيقة مبنية على فيزياء أرسطو إلى حقيقة مبنية على الفيزياء الرياضية والاستنباطية بعد عمل ابن الشاطر. لذا تميزت ثورة مراغة بالابتعاد عن الأسس الفلسفية لكونيات أرسطو وفلك بطليموس والاتجاه نحو التركيز على الملاحظة التجريبية وترضية الفلك وبشكل عام الطبيعة كما جاء في أعمال ابن الشاطر والقوشجي والبيجرندي والخافري.[92][93][94]
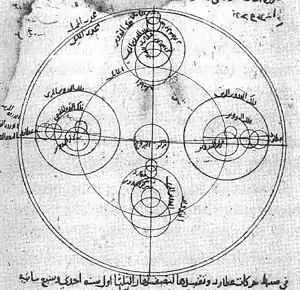
تضمنت إنجازات مدرسة مراغة أول دليل رصدي تجريبي لدوران الأرض حول محورها وكان ورائه الطوسي والقوشجي[14] والفصل بين فلسفة الطبيعة وعلم الفلك الذي قام به ابن الشاطر والقوشجي[15] وتفنيد ابن الشاطر لنظام بطليموس على أسس تجريبية لا فلسفية[88] وتطوير نظام لا بطليموسي، من قبل ابن الشاطر أيضا، والذي كان رياضيا مطابقا لنظام كوبرنيكوس شمسي المركز.[95]
كان محيي الدين الأوردي (و 1266) الأول بين علماء مراغة في تطوير نظام لا بطليموسي واقترح نظرية جديدة سماها لامة الأوردي.[96] حل نصير الدين الطوسي (1201-1274) مسائل مهمة في نظام بطليموس عبر مزدوجة الطوسي التي أوجدها كبديل لمسألة الإكوانت الفيزيائية لبطليموس.[97] ناقش تلميذ الطوسي، قطب الدين الشيرازي (1236-1311) في كتابه نهاية الإدراك في دراية الأفلاك، إمكانية مركزية الشمس. كتب القزويني الكاتبي (و 1277)، والذي عمل أيضا في مرصد مراغة، في كتابه حكمة العين داعما بحجج للنظام شمسي المركز لكنه ترك فيما بعد الفكرة.[79]
أدرج ابن الشاطر الدمشقي (1304-1375)، في كتابه نهاية السؤال في تصحيح الأصول، لامة الأوردي وألغى الحاجة إلى الإيكوانت عبر استحداث فلك تدوير جديد (مزدوجة الطوسي) فابتعد عن نظام بطليموس بطريقة رياضية مماثلة لطريقة نيكولاس كوبرنيكوس في القرن السادس عشر. وعكس علماء الفلك الذين سبقوه، لم يكن ابن الشاطر متمسكا بالأسس النظرية لفلسفة الطبيعة أو لعلم كونيات أرسطو بل اهتم فقط بتطوير نظام متلائم مع الملاحظات الاستنباطية. فعلى سبيل المثال، قادت ابن الشاطر دقة ملاحظته إلى إلغاء فلك التدوير في نظام بطليموس الشمسي وكل التباينات المركزية وفلكات التدوير والإيكوانت في نظام بطليموس القمري. وبذلك أصبح نظامه أكثر ملائمة للملاحظات الاستنباطية من أي نظام سابق[88] وأصبح كذلك أول نظام يسمح بالتجريب الاستنباطي.[98]
المراصد
الأدوات
الأسطرلابات والبلانيسفير
كانت الأسطرلابات النحاسية تستعمل في شتى أنحاء العالم الإسلامي وظلك لإيجاد القبلة. يرجع أقدم أسطرلاب عربي معروف إلى 315 حسب التقويم الهجري. أول شخص يرجع له الفضل في صناعة أسطرلاب في العالم الإسلامي هو محمد الفزاري.[99] رغم أن أول من اخترعوا الأسطرلاب كانوا الهلينيين، أسهم الفزاري كثيرا في الأسطرلاب حيث أدخل عليه مقاييس زاوية[100] وأضاف دوائر تشير إلى السمت في الأفق.[101] وفي فترة الخلافة العباسية أتقن العرب الأسطرلاب وصناعته حيث عرفوا بالتحديد بداية رمضان ومواقيت الصلاة واتجاه مكة (القبلة) واستخدموه أكثر من ألف استخدام. في القرن العاشر، وصف عبد الرحمن بن عمر الصوفي الاستعمالات الأكثر من الألف للأسطرلاب في مجالات متنوعة ومنها الفلك والتنجيم والملاحة والمساحة وحساب الوقت والصلاة والقبلة إلخ.
- الأسطرلاب الكبير
رصد ابن يونس في القرن العاشر أكثر من 10000 مدخل لمواضع الشمس لسنوات عديدة مستعملا أسطرلابا كبيرا قطره 1.4 متر.[48]
- الأسطرلاب الموجه ميكانيكيا
اخترع ابن سهم أول أسطرلاب ميكانيكي ذي تروس في العالم الإسلامي. كما صنع أبو الريحان البيروني جهازا مماثلا بثمانية تروس في 996 ويمكن اعتباره سلف الساعات الميكانيكية التي اخترعها المهندسون المسلمون لاحقا.[102]
- الأسطرلاب العمودي
اخترع أبو الريحان البيروني أول أسطرلاب عمودي في العقد الأول من القرن الحادي عشر.
- الأسطرلاب الموحد
- الزورقي
الزورقي هو أسطرلاب فريد من نوعه اخترعه السجزي من أجل دعم نظريته بمركزية الشمس وفيه الأرض هي التي تتحرك لا السماء.[52]

- البلانيسفير
في بداية القرن الحادي عشر اخترع البيروني أيضا أول بلانسفير الذي يعتبر حاسبا تناظريا أوليا وكتب مقالة حوله.[103] وكان الأسطرلاب سلف البلانسفير الحديث.
- الأسطرلاب الخطي
ذكر شرف الدين الطوسي في كتاب له أصاف الأسطرلاب العمودي الذي اخترعه والذي يعرف في بعض الأحيان أمر الطوسي.[104]
الأسطرلاب الكروي
لقـد صنف أبو عبيد الله الروداني مؤلفاً في صنع الأسطرلاب كتاباً سماه تحفة أولي الألبـاب فـي العمـل بالأسطرلاب الذي بقي طويلا يستعمل لقياس مواضع الكواكب وتحديد سـيرها، وكذلك لمراقبة حالة الجو وشئون الملاحة.
الحاسبات التناظرية
تم اختراع عدة حاسبات تناظرية لحساب دوائر عرض الشمس والقمر والكواكب ومسار الشمس والوقت من النهار الذي ستظهر فيه الاقترانات الكوكبية ولأداء الاستيفاء الخطي.
- البيون
كان البيون حاسبا تناظريا اخترعه إبراهيم بن يحيى الزرقالي في الأندلس حوالي 1015 ميلادية ويعتبر أداة ميكانيكية لحساب خطوط طول ومنازل القمر والشمس والكواكب بدون استعمال تمثيل هندسي للموضع الأصلي والبعد الزاوي للجرم السماوي.[105]
- حاسب التقويم الموجه ميكانيكيا
اخترع أيضا أبو الريحان البيروني أول حاسب ميكانيكي للتقويم الشمسي القمري والذي يعمل بدوران ثمانية تروس-عجلات.[106] ويعتبر هذا الاختراع سلفا لآلة معرفية ثابتة ومسلكة.[107]
- عجلة خريطة
العجلة الخريطة، والتي تعرف عند الغرب باسم فولفيل (بالإنجليزية: Volvelle) وهي خريطة حاسبة بها أجزاء تدور ويعتبرها الكثيرون سلفا للحاسب التناظري من الورق.[108] يمكن اقتفاء أثر العجلة الخريطة في بعض الأطروحات العربية حول الطب الخلطي[109] وفي أعمال البيروني (ح. 1000) الذي قام بإسهامات هامة في العجلة الخريطة.[110] في القرن العشرين كان لا يزال للعجلة الخريطة عدة استعمالات.
- المقلوزة
- ساعة القلعة بالحاسب التناظري المبرمج
- الأسطرلاب الميكانيكي بحاسب التقويم الموجه
- طبق الاقتران
- حاسب كوكبي
الساعات الفلكية
- الساعة الفلكية المائية
- الساعة الفلكية بالنوابض
- المنبه الميكانيكي للساعة
- الساعة الفلكية الرصدية
المزولات
- المزولة
- مزولة الفرجار
وصلات داخلية
المراجع
- (Saliba 1994b, pp. 245, 250, 256–257)
- (Gingerich 1986)
- Leichter, Joseph (May 2004). "The Zij as-Sanjari of Gregory Chioniades". أرشيف الإنترنت. Providence, RI: جامعة براون (نشر 27 June 2009). مؤرشف من الأصل في 05 أبريل 2019. اطلع عليه بتاريخ 11 نوفمبر 2016. الوسيط
|CitationClass=تم تجاهله (مساعدة); تحقق من التاريخ في:|تاريخ أرشيف=(مساعدة) - Sharma, Virendra Nath (1995), Sawai Jai Singh and His Astronomy, Motilal Banarsidass Publ., صفحات 8–10, ISBN 8120812565 الوسيط
|CitationClass=تم تجاهله (مساعدة); الوسيط|separator=تم تجاهله (مساعدة)CS1 maint: ref=harv (link) - Saliba (1999).
- van Dalen, Benno (2002), "Islamic Astronomical Tables in China: The Sources for Huihui li", in Ansari, S. M. Razaullah (المحرر), History of Oriental Astronomy, سبرنجر, صفحات 19–32, ISBN 1402006578 الوسيط
|CitationClass=تم تجاهله (مساعدة); الوسيط|separator=تم تجاهله (مساعدة)CS1 maint: ref=harv (link) - African Cultural Astronomy By Jarita C. Holbrook, R. Thebe Medupe, Johnson O. Urama نسخة محفوظة 30 مارس 2015 على موقع واي باك مشين.
- The Timbuktu Astronomy Project نسخة محفوظة 26 مايو 2020 على موقع واي باك مشين. [وصلة مكسورة]
- "Arabic Star Names". Islamic Crescents' Observation Project. 2007-05-01. مؤرشف من الأصل في 18 أغسطس 2018. اطلع عليه بتاريخ 24 يناير 2008. الوسيط
|CitationClass=تم تجاهله (مساعدة) - (Ilyas 1997)
- Ahmad, I. A. (1995), "The impact of the Qur'anic conception of astronomical phenomena on Islamic civilization", Vistas in Astronomy, 39 (4): 395–403, doi:10.1016/0083-6656(95)00033-X الوسيط
|CitationClass=تم تجاهله (مساعدة); الوسيط|separator=تم تجاهله (مساعدة)CS1 maint: ref=harv (link) - Ahmad, I. A. (June 3, 2002), "The Rise and Fall of Islamic Science: The Calendar as a Case Study", Faith and Reason: Convergence and Complementarity (PDF), جامعة الأخوين, مؤرشف من الأصل (PDF) في 3 مارس 2016, اطلع عليه بتاريخ 31 يناير 2008 الوسيط
|CitationClass=تم تجاهله (مساعدة); الوسيط|separator=تم تجاهله (مساعدة)CS1 maint: ref=harv (link) - Michene, James A. (May 1955), "Islam: The Misunderstood Religion", ريدرز دايجست: 68–70 الوسيط
|CitationClass=تم تجاهله (مساعدة); الوسيط|separator=تم تجاهله (مساعدة)CS1 maint: ref=harv (link) - (Ragep 2001a)
- (Ragep 2001b)
- (Huff 2003, p. 175)
- سورة التوبة آية 36
- سورة البقرة آية 189
- Syed Mohammad Hussain Tabatabai, "Volume 3: Surah Baqarah, Verse 189", Tafsir al-Mizan, مؤرشف من الأصل في 29 مايو 2016, اطلع عليه بتاريخ 24 يناير 2008 الوسيط
|CitationClass=تم تجاهله (مساعدة); الوسيط|separator=تم تجاهله (مساعدة)CS1 maint: ref=harv (link) - Khalid Shaukat (September 23, 1997). "The Science of Moon Sighting". مؤرشف من الأصل في 09 نوفمبر 2012. اطلع عليه بتاريخ 24 يناير 2008. الوسيط
|CitationClass=تم تجاهله (مساعدة); تحقق من التاريخ في:|تاريخ أرشيف=(مساعدة) - سورة البقرة آية 144
- سورة البقرة آية 150
- Syed Mohammad Hussain Tabatabai, "Tafsir Al-Mizan - Allamah Muhammad Hussein Tabatabai" en, Tafsir al-Mizan, مؤرشف من الأصل في 29 يوليو 2007, اطلع عليه بتاريخ 24 يناير 2008 الوسيط
|CitationClass=تم تجاهله (مساعدة); الوسيط|separator=تم تجاهله (مساعدة);|chapter=تم تجاهله (مساعدة); Invalid|script-title=: missing prefix (مساعدة)CS1 maint: ref=harv (link) - The history of the telescope Henry C. King, Harold Spencer Jones, Courier Dover Publications, 2003 ISBN 0-486-43265-3, 9780486432656
- Kamel Ben Salem (2007), "The Evolution of the Universe: A New Vision" (PDF), European Journal of Science and Theology, مؤرشف من الأصل (PDF) في 29 مايو 2016, اطلع عليه بتاريخ 19 مارس 2010 الوسيط
|CitationClass=تم تجاهله (مساعدة); الوسيط|separator=تم تجاهله (مساعدة)CS1 maint: ref=harv (link) - "References". 1001 Inventions. مؤرشف من الأصل في 25 يوليو 2011. اطلع عليه بتاريخ 22 يناير 2008. الوسيط
|CitationClass=تم تجاهله (مساعدة) - سورة الأنبياء آية 30
- سورة الذاريات آية 47
- سورة النازعات آية 30
- Rashad Khalifa (2001), Quran: the final testament, صفحة 497, ISBN 1881893057 الوسيط
|CitationClass=تم تجاهله (مساعدة); الوسيط|separator=تم تجاهله (مساعدة)CS1 maint: ref=harv (link) - (Dallal 1999, p. 162)
- What is the Hijrah Calendar? نسخة محفوظة 06 يناير 2017 على موقع واي باك مشين.
- هذا الكتاب غير مرتبط بكتاب الخوارزمي زيج السند.(Kennedy 1956)
- (King 2002, p. 240)
- "Greek Astronomy". مؤرشف من الأصل في 13 مايو 2019. اطلع عليه بتاريخ 15 يناير 2008. الوسيط
|CitationClass=تم تجاهله (مساعدة) - "Almagest". The Internet Encyclopedia of Science. مؤرشف من الأصل في 13 أكتوبر 2018. اطلع عليه بتاريخ 15 يناير 2008. الوسيط
|CitationClass=تم تجاهله (مساعدة) - O'Connor, John J.; Robertson, Edmund F. (November 1999), "Abu Said Sinan ibn Thabit ibn Qurra", تاريخ ماكتوتور لأرشيف الرياضيات الوسيط
|CitationClass=تم تجاهله (مساعدة); الوسيط|separator=تم تجاهله (مساعدة)CS1 maint: ref=harv (link) - (Dallal 1999, p. 163)
- Langermann, Y. Tzvi (1985), "The Book of Bodies and Distances of Habash al-Hasib", Centaurus, 28: 108–128 [112] الوسيط
|CitationClass=تم تجاهله (مساعدة); الوسيط|separator=تم تجاهله (مساعدة)CS1 maint: ref=harv (link) - Langermann, Y. Tzvi (1985), "The Book of Bodies and Distances of Habash al-Hasib", Centaurus, 28: 108–128 [111] الوسيط
|CitationClass=تم تجاهله (مساعدة); الوسيط|separator=تم تجاهله (مساعدة)CS1 maint: ref=harv (link) - (Dallal 1999, p. 164)
- (Singer 1959, p. 151)
- (Wickens 1976, pp. 117–18) "نسخة مؤرشفة". Archived from the original on 9 ديسمبر 2012. اطلع عليه بتاريخ 28 مايو 2010. الوسيط
|CitationClass=تم تجاهله (مساعدة)صيانة CS1: BOT: original-url status unknown (link) - 23rd Annual Conference on the History of Arabic Science, حلب, سوريا, October 2001 الوسيط
|CitationClass=تم تجاهله (مساعدة); الوسيط|separator=تم تجاهله (مساعدة)CS1 maint: ref=harv (link) (cf. (Zaimeche 2002)) - Kepple, George Robert (1998). The Night Sky Observer's Guide, Volume 1. Willmann-Bell, Inc. صفحة 18. ISBN 0-943396-58-1. الوسيط
|CitationClass=تم تجاهله (مساعدة) - "Observatoire de Paris (Abd-al-Rahman Al Sufi)". مؤرشف من الأصل في 09 أكتوبر 2018. اطلع عليه بتاريخ 19 أبريل 2007. الوسيط
|CitationClass=تم تجاهله (مساعدة); تحقق من التاريخ في:|تاريخ أرشيف=(مساعدة) - "Observatoire de Paris (LMC)". مؤرشف من الأصل في 08 فبراير 2019. اطلع عليه بتاريخ 19 أبريل 2007. الوسيط
|CitationClass=تم تجاهله (مساعدة); تحقق من التاريخ في:|تاريخ أرشيف=(مساعدة) - (Zaimeche 2002)
- Aulie, Richard P. (March 1994), "Al-Ghazali Contra Aristotle: An Unforeseen Overture to Science In Eleventh-Century Baghdad", Perspectives on Science and Christian Faith, 45, صفحات 26–46 الوسيط
|CitationClass=تم تجاهله (مساعدة); الوسيط|separator=تم تجاهله (مساعدة)CS1 maint: ref=harv (link) (cf. "References". 1001 Inventions. مؤرشف من الأصل في 25 يوليو 2011. اطلع عليه بتاريخ 22 يناير 2008. الوسيط|CitationClass=تم تجاهله (مساعدة)) - Shlomo Pines (1986), Studies in Arabic versions of Greek texts and in mediaeval science, 2, دار بريل للنشر, صفحات viii & 201–17, ISBN 9652236268 الوسيط
|CitationClass=تم تجاهله (مساعدة); الوسيط|separator=تم تجاهله (مساعدة)CS1 maint: ref=harv (link) - Bartel Leendert van der Waerden (1987). "The Heliocentric System in Greek, Persian and Hindu Astronomy", Annals of the New York Academy of Sciences 500 (1), 525–545 [534-537].
- (Nasr 1993, pp. 135-136)
- Craig, William Lane (June 1979), "Whitrow and Popper on the Impossibility of an Infinite Past", The British Journal for the Philosophy of Science, 30 (2): 165–170 [165–6], doi:10.1093/bjps/30.2.165 الوسيط
|CitationClass=تم تجاهله (مساعدة); الوسيط|separator=تم تجاهله (مساعدة)CS1 maint: ref=harv (link) - (Saliba 1994a, p. 116)
- (Huff 2003, p. 57)
- (Huff 2003, p. 326)
- Toomer, G. J. (December 1964), "Review: Ibn al-Haythams Weg zur Physik by Matthias Schramm", Isis, 55 (4): 463–465 [463–4], doi:10.1086/349914 الوسيط
|CitationClass=تم تجاهله (مساعدة); الوسيط|separator=تم تجاهله (مساعدة)CS1 maint: ref=harv (link) - (Rosen 1985, pp. 19-20 & 21)
- Josep Puig Montada (September 28, 2007). "Ibn Bajja". موسوعة ستانفورد للفلسفة. مؤرشف من الأصل في 05 مايو 2019. اطلع عليه بتاريخ 11 يوليو 2008. الوسيط
|CitationClass=تم تجاهله (مساعدة); تحقق من التاريخ في:|تاريخ أرشيف=(مساعدة) - Mohamed, Mohaini (2000), Great Muslim Mathematicians, Penerbit UTM, صفحات 49–50, ISBN 9835201579 الوسيط
|CitationClass=تم تجاهله (مساعدة); الوسيط|separator=تم تجاهله (مساعدة)CS1 maint: ref=harv (link) - Hamid-Eddine Bouali, Mourad Zghal, Zohra Ben Lakhdar (2005). "Popularisation of Optical Phenomena: Establishing the First Ibn Al-Haytham Workshop on Photography" (PDF). The Education and Training in Optics and Photonics Conference. مؤرشف من الأصل (PDF) في 05 أكتوبر 2018. اطلع عليه بتاريخ 08 يوليو 2008. الوسيط
|CitationClass=تم تجاهله (مساعدة); تحقق من التاريخ في:|تاريخ أرشيف=(مساعدة)صيانة CS1: أسماء متعددة: قائمة المؤلفون (link) - Dr. A. Zahoor (1997). "Abu Raihan Muhammad al-Biruni". Hasanuddin University. مؤرشف من الأصل في 18 يناير 2008. الوسيط
|CitationClass=تم تجاهله (مساعدة) - O'Connor, John J.; Robertson, Edmund F., "Abu Rayhan Muhammad ibn Ahmad al-Biruni", تاريخ ماكتوتور لأرشيف الرياضيات الوسيط
|CitationClass=تم تجاهله (مساعدة); الوسيط|separator=تم تجاهله (مساعدة)CS1 maint: ref=harv (link) - (Sabra 1998, pp. 293-8)
- A. Abd-Allah. "The Qur'an, Knowledge, and Science". جامعة كاليفورنيا الجنوبية. مؤرشف من الأصل في 28 نوفمبر 2008. اطلع عليه بتاريخ 22 يناير 2008. الوسيط
|CitationClass=تم تجاهله (مساعدة) - (Sabra 1998, pp. 317-18)
- (Ragep, Teresi & Hart 2002)
- (Saliba 1994b, pp. 60 & 67-69)
- Livingston, John W. (1971), "Ibn Qayyim al-Jawziyyah: A Fourteenth Century Defense against Astrological Divination and Alchemical Transmutation", Journal of the الجمعية الشرقية الأمريكية, 91 (1): 96–103, doi:10.2307/600445 الوسيط
|CitationClass=تم تجاهله (مساعدة); الوسيط|separator=تم تجاهله (مساعدة)CS1 maint: ref=harv (link) - Livingston, John W. (1971), "Ibn Qayyim al-Jawziyyah: A Fourteenth Century Defense against Astrological Divination and Alchemical Transmutation", Journal of the American Oriental Society, 91 (1): 96–103 [99], doi:10.2307/600445 الوسيط
|CitationClass=تم تجاهله (مساعدة); الوسيط|separator=تم تجاهله (مساعدة)CS1 maint: ref=harv (link) - كتاب مفتاح دار السعادة لابن قيم الجوزية ص 235
- (Iqbal & Berjak 2003)
- (Zaimeche 2002, p. 7)
- (Sabra 1998, pp. 294-5)
- (Sabra 1998, p. 300)
- (Langermann 1990, pp. 25-34)
- (Duhem 1969, p. 28)
- (Nasr 1993, p. 135, n. 13)
- (Baker & Chapter 2002)
- (Marmura 1965)
- G. Wiet, V. Elisseeff, P. Wolff, J. Naudu (1975). History of Mankind, Vol 3: The Great medieval Civilisations, p. 649. George Allen & Unwin Ltd, يونيسكو.
- (Covington 2007)
- (Nasr 1993, p. 134)
- (Sabra 1998, pp. 305-306)
- (Saliba 1981, p. 219)
- Sabra, A. I., "The Andalusian Revolt Against Ptolemaic Astronomy: Averroes and al-Bitrûjî", in Mendelsohn, Everett (المحرر), Transformation and Tradition in the Sciences: Essays in honor of I. Bernard Cohen, مطبعة جامعة كامبريدج, صفحات 233–53 الوسيط
|CitationClass=تم تجاهله (مساعدة); الوسيط|separator=تم تجاهله (مساعدة)CS1 maint: ref=harv (link) - Bernard R. Goldstein, ed., Al-Biţrūjī: On the Principles of Astronomy, (New Haven: Yale University Press, 1971), pp. 6-14.
- (Saliba 1994b, pp. 233-234 & 240)
- (Dallal 1999, p. 171)
- (Saliba 1994b, pp. 245, 250, 256-257)
- Saliba, George (Autumn 1999), "Seeking the Origins of Modern Science?", BRIIFS, 1 (2), مؤرشف من الأصل في 4 أكتوبر 2012, اطلع عليه بتاريخ 25 يناير 2008 الوسيط
|CitationClass=تم تجاهله (مساعدة); الوسيط|separator=تم تجاهله (مساعدة)CS1 maint: ref=harv (link) - (Saliba 1994b, pp. 42 & 80)
- Dallal, Ahmad (2001–2002), The Interplay of Science and Theology in the Fourteenth-century Kalam, From Medieval to Modern in the Islamic World, Sawyer Seminar at the جامعة شيكاغو, مؤرشف من الأصل في 10 فبراير 2012, اطلع عليه بتاريخ 02 فبراير 2008 الوسيط
|CitationClass=تم تجاهله (مساعدة); الوسيط|separator=تم تجاهله (مساعدة)CS1 maint: ref=harv (link) صيانة CS1: تنسيق التاريخ (link) - (Huff 2003, pp. 217-8)
- (Saliba 1994b, pp. 254 & 256–257)
- (Saliba 1979)
- (Gill 2005)
- Faruqi, Y. M. (2006). "Contributions of Islamic scholars to the scientific enterprise". International Education Journal. 7 (4): 395–396. الوسيط
|CitationClass=تم تجاهله (مساعدة) - ريتشارد فراي, Golden Age of Persia, p. 163.
- L. C. Martin (1923), Surveying and navigational instruments from the historical standpoint, 24, صفحات 289–303 [289], doi:10.1088/1475-4878/24/5/302 الوسيط
|CitationClass=تم تجاهله (مساعدة); الوسيط|separator=تم تجاهله (مساعدة)CS1 maint: ref=harv (link) - Victor J. Katz & Annette Imhausen (2007), The mathematics of Egypt, Mesopotamia, China, India, and Islam: a sourcebook, دار نشر جامعة برنستون, صفحة 519, ISBN 0691114854 الوسيط
|CitationClass=تم تجاهله (مساعدة); الوسيط|separator=تم تجاهله (مساعدة)CS1 maint: ref=harv (link) - "Islam, Knowledge, and Science". جامعة كاليفورنيا الجنوبية. مؤرشف من الأصل في 18 فبراير 2009. اطلع عليه بتاريخ 22 يناير 2008. الوسيط
|CitationClass=تم تجاهله (مساعدة) - ويل ديورانت (1950). قصة الحضارة (كتاب) IV: The Age of Faith, p. 239-45.
- "Linear astrolabe", [[موسوعة بريتانيكا]], 2007, مؤرشف من الأصل في 29 أبريل 2008, اطلع عليه بتاريخ 22 يناير 2008 الوسيط
|CitationClass=تم تجاهله (مساعدة); الوسيط|separator=تم تجاهله (مساعدة); وصلة إنترويكي مضمنة في URL العنوان (مساعدة)CS1 maint: ref=harv (link) - (Hassan)
- (Hill 1985)
- Tuncer Oren (2001). "Advances in Computer and Information Sciences: From Abacus to Holonic Agents", Turk J Elec Engin 9 (1): 63–70 [64].
- Nick Kanas, VOLVELLES! Early Paper Astronomical Computers, مؤرشف من الأصل في 29 مايو 2016, اطلع عليه بتاريخ 13 أكتوبر 2009 الوسيط
|CitationClass=تم تجاهله (مساعدة); الوسيط|separator=تم تجاهله (مساعدة)CS1 maint: ref=harv (link) - ديفيد خان (كاتب) (March 1980), "On the Origin of Polyalphabetic Substitution", Isis, دار نشر جامعة شيكاغو, 71 (1): 122–127 [126], doi:10.1086/352410, مؤرشف من الأصل في 9 ديسمبر 2019, اطلع عليه بتاريخ 13 أكتوبر 2009 الوسيط
|CitationClass=تم تجاهله (مساعدة); الوسيط|separator=تم تجاهله (مساعدة)CS1 maint: ref=harv (link) - Bryan S. Turner (March 1987), "State, Science and Economy in Traditional Societies: Some Problems in Weberian Sociology of Science", British Journal of Sociology, Blackwell Publishing, 38 (1): 1–23 [12], doi:10.2307/590576, مؤرشف من الأصل في 7 ديسمبر 2019, اطلع عليه بتاريخ 13 أكتوبر 2009 الوسيط
|CitationClass=تم تجاهله (مساعدة); الوسيط|separator=تم تجاهله (مساعدة)CS1 maint: ref=harv (link)
- بوابة القمر
- بوابة علم الكون
- بوابة علم الفلك
- بوابة المجموعة الشمسية
- بوابة الفضاء
- بوابة المريخ
- بوابة نجوم
- بوابة تاريخ العلوم
- بوابة المشتري
- بوابة علوم إسلامية
- بوابة أورانوس
- بوابة رحلات فضائية


_01.jpg.webp)