دالة القواسم
في الرياضيات وبالتحديد في نظرية الأعداد، دالة القواسم (بالإنجليزية: Divisor function) هي دالة حسابية تتعلق بقواسم عدد صحيح ما.[1] تساوي هذه الدالة عددَ قواسم عدد طبيعي ما n، بما فيهن الواحد والعدد نفسه. تظهر هذه الدالة في العديد من المتطابقات المهمة، منها العلاقة التي تربط دالة زيتا لريمان بمتسلسلة أيزنشتاين للأشكال النمطية.
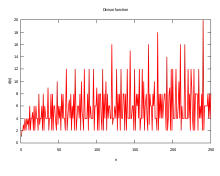
دالة القواسم (σ0(n حتى n = 250
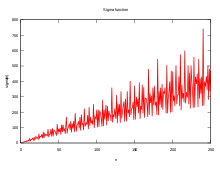
دالة سيغما (σ1(n حتى n = 250
درس هذه الدالةَ عالم الرياضيات الهندي سرينفاسا أينجار رامانجن. انظر إلى مجموع رامانجن.
تعريف
مثال
σ0(12) هي عدد قواسم العدد 12.
خصائص
hjjhhhhhhhfuuuuuhuuuuuukktyyh
انظر أيضًا
- مؤشر أويلر، أو ما يعرف بدالة في لأويلر.
- جدول القواسم
مراجع
- بوابة نظرية الأعداد
- "معلومات عن دالة القواسم على موقع mathworld.wolfram.com". mathworld.wolfram.com. مؤرشف من الأصل في 8 سبتمبر 2019. الوسيط
|CitationClass=تم تجاهله (مساعدة) - "Divisor function". Wikipedia (باللغة الإنجليزية). 2020-08-31. مؤرشف من الأصل في 7 ديسمبر 2020. الوسيط
|CitationClass=تم تجاهله (مساعدة)
دالة القواسم في المشاريع الشقيقة
 صور وملفات صوتية من كومنز
صور وملفات صوتية من كومنز
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.
