تمثيل القبولية
تمثيل القبولية أو تمثيل المسامحة أو تمثيل فايرستون، هو أحد التمثيلات الكهربية الميكانيكية الشائعة، ولكن الأكثر شيوعًا هو تمثيل المعاوقة، والفرق بينهما هو اختلاف التمثيلات الميكانيكية لفرق الجهد والتيارالكهربي، حيث يمكن تطبيق طريقة "إقلاب الدوائر" للتحويل من تمثيل القبولية إلى تمثيل المعاوقة، يحافظ تمثيل القبولية على طوبولوجيا النظام الميكانيكي عندما يُحوَّل إلى المجال الكهربي، على عكس تمثيل المعاوقة، وعلى الجانب الآخر يحافظ تمثيل المعاوقة على التماثل بين المعاوقة الكهربائية والمعاوقة الميكانيكية على عكس تمثيل القبولية.

تاريخيًا، بدأ استخدام تمثيل المعاوقة قبل تمثيل القبولية بوقت طويل، طُرح مصطلح القبولية الميكانيكية كمفهوم متعلق بالقابلية للحركة الميكانيكية بواسطة فلويد ألبورن فايرستون في عام 1932، وكان طرحه يهدف إلى الحفاظ على طوبولوجيا التمثيل الكهربي الميكانيكي.
يُستخدَم تمثيل الأنظمة الميكانيكية على شكل دوائر كهربائية للاستفادة من التطورات النظرية الهائلة في تحليل الأنظمة الكهربائية المُعقدة، وخاصةً في مجال المرشحات،[2] بتحويل النظام الميكانيكي إلى صيغة كهربائية يمكن تطبيق قواعد هندسة الدوائر الكهربية مباشرةً النظام الميكانيكي دون تعديل، بالإضافة إلى أهمية استخدام التمثيل الكهربي الميكانيكي في الأنظمة الكهروميكانيكية؛ عن طريق تحويل الجزء الميكانيكي من النظام إلى صيغة كهربائية وبذلك يمكن إجراء تحليل واحد للنظام بأكمله.
عند تطبيق هذه الطريقة يكون السلوك الرياضي للنظام الكهربي المُحاكى مطابقًا للنظام الميكانيكي المُمثَّل، وكل عنصر في المجال الكهربي لديه عنصر مقابل في المجال الميكانيكي، وبالتالي جميع قوانين تحليل الدوائر الكهربية - مثل قوانين كيرشوف التي تُطبَّق في المجال الكهربي - يمكن تطبيقها أيضًا على النظام الميكانيكي المُمثَّل.
نبذة تاريخية
تاريخيًا، بدأ استخدام تمثيل المعاوقة قبل تمثيل القبولية بوقت طويل، طُرح مصطلح القبولية الميكانيكية كمفهوم متعلق بالقابلية للحركة الميكانيكية بواسطة فلويد ألبورن فايرستون في عام 1932، وكان طرحه يهدف إلى الحفاظ على طوبولوجيا التمثيل الكهربي الميكانيكي،[3][4] في ذات الوقت كان دبليو. هاهنيل يطرح ذات الفكرة بشكل مستقل في ألمانيا، التقت هوراس ترينت الفكرة، وطوّرها باستخدام نظرية المخططات، حتى أنتج تمثيلًا جديدًا عُرف بتمثيل ترينت.[5][6]
العناصر
قبل البدء بعملية التمثيل الكهربي للنظام الميكانيكي؛ يجب وصف الشبكة الميكانيكية، بمجموعة من العناصر المثالية، ثم يتم استبدال كل عنصر بالعنصر الكهربي المناظر له.[7] الرموز المستخدمة لهذه العناصر الميكانيكية موضحة في الصور التوضيحية في الأقسام التالية.
يتم التمثيل حسب نموذج العناصر المُجمع، حيث نفترض أن العنصر الميكانيكي الذي تتم عليه العملية صغير جدًا لدرجة أن الزمن الذي تستغرقه الموجات الميكانيكية للمرور بين طرفيه يمكن إهمالها. يمكن أيضًا إجراء التمثيل حسب نموذج العناصر المُوزع مثلما يُطيق في تحليل خطوط النقل؛ لكن مميزات نموذج العناصر المُجمع أكبر. تُمثل العناصر الميكانيكية المُجمعة بثلاثة عناصر كهربية رئيسية هي المقاومة، والحث، والسعة، ويُختار "متغير جهد" ليتم تمثيله بفرق الجهد الكهربي، و"متغير تدفق" ليتم تمثيله بالتيار الكهربي،[8] في تمثيل القبولية متغير الجهد هو السرعة ومتغير التدفق هو القوة.[9] تُعرف المعاوقة الميكانيكية بأنها النسبة بين القوة والسرعة، وبالتالي فلا يمكن تمثيلها بالمقاومة الكهربائية (وهي النسبة بين فرق الجهد والتيار الكهربي)، ولكن في هذه الحالة يُماثلها المسامحة الكهربائية (معكوس المقاومة)، كما إن فكرة القبولية الميكانيكية أكثر شيوعا في النظام الميكانيكي أكثر من المقاومة،[10] ومن هنا جاءت التسمية بتمثيل القبولية.[11]
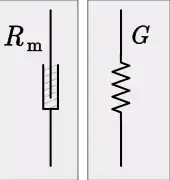
المقاومة
يُمثل "فقدان الطاقة في النظام الميكانيكي نتيجة عمليات مثل الاحتكاك" بـ"الموصلية الكهربائية"، والمكون الميكانيكي المماثل الذي يعبر بالمقاومة الميكانيكية هو ممتص الصدمات أو الذي يؤدي وظيفة التخميد. القانون الذي يوضح العلاقة بين المقاومة الكهربية والضيغ الفيزيائية الأخرى هو قانون أوم:
والمعادلة المماثلة في المجال الميكانيكي:
- حيث: G = 1/R هي الموصلية الكهربية، وR هي المقاومة، وv هو فرق الجهد، وi هو التيار الكهربي، وRm هي المقاومة الميكانيكية، أو التخميد، وF هي القوة، وu هي السرعة الناجمة عن القوة.
الموصلية الكهربية هي الجزء الحقيقي من القبولية الكهربائية، وبالمثل المقاومة الميكانيكية هي الجزء الحقيقي من المقاومة الميكانيكية.[14]
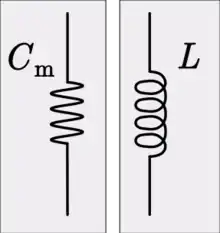
الحث
الكمية الميكانيكية التي يتم تمثيلها بـ"الحث" في تمثيل القبولية هي هي المطاوعة وهي مقلوب الجساءة، وعلى ذلك يمكن تمثيل المحث في المجال الكهربي بالنابض أو الزُنْبُرُك في المجال الميكانيكي. ويخضع للمعادلة:
والمعادلة المماثلة في المجال الميكانيكي هي قانون هوك:
- حيث: L هو الحث، وt هو الزمن، وCm = 1/S هي المطاوعة الميكانيكية، وS هي الجساءة.[16]
معاوقة المحث هي قيمة خيالية يُعبر عنها بالمعادلة:
والمعادلة المماثلة في المجال الميكانيكي:
- حيث: Z هي المعاوقة الكهربائية، وj هو الوحدة التخيلية، وω هو التردد الزاوي، وYm هي المعاوقة الميكانيكية.[17]
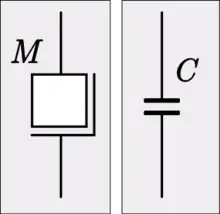
السعة
الكمية الميكانيكية التي يتم تمثيلها بـ"السعة" هي الكتلة، وعلى ذلك يمكن تمثيل المكثف في المجال الكهربي بالمكثف. تخضع السعة الكهربية للمعادلة:
والمعادلة المماثلة في المجال الميكانيكي هي قانون نيوتن الثاني للحركة:
- حيث: C هي السعة، وM هي الكتلة.
معاوقة المكثف هي قيمة خيالية يُعبر عنها بالمعادلة:
والمعادلة المماثلة في المجال الميكانيكي:[19]
المقاصرة
هناك مشكلة منطقية في تمثيل الكتلة الميكانيكية بعنصر كهربي، وهذه المشكلة متعلقة بحقيقة أن سرعة النظام الميكانيكي (ومشتقاتها خاصة العجلة) تُقاس دائمًا بالنسبة لإطار مرجعي ثابت - عادة الأرض وجاذبيتها - فعندما تكون السرعة لها قيمة "u" عند نقطة معينة؛ تماثل بفرق جهد معين، وعندما تساوي السرعة صفر عند نقطة أخرى تعتبر هذه النقطة بمثابة الجهد المرجعي (الأرضي)، وحينها لا نستطيع تمثيل الكتلة بمكثف غير متصل بالجهد المرجعي.[20] لا تقتصر صعوبة تمثيل الكتلة على تمثيل القبولية فقط، فذات المشكلة تحدث في تمثيل المعاوقة، ولكن في هذه الحالة ستُمثَّل بمحث غير متصل بالجهد المرجعي، وهو ما لا يمكن تمثيله بالعناصر القياسية.[21]
دفعت هذه المعضلة مالكوم كلايف سميث البروفيسور في جامعة كامبريدج في عام 2002 إلى ابتكار عنصر ميكانيكي جديد مخزن للطاقة يسمى المقاصرة - مشتق من القصور - (بالإنجليزية: inertance)، يمكن لهذا العنصر الجديد أن يكون لطرفيه سرعتان مختلفتان وعجلتان مختلفتان - على عكس الكتلة -، المعادلة التي تصف المقاصرة:[22]
- حيث: F هي القوة الواقعة على الطرفين، وB هي المقاصرة، وu1 وu2 هي سرعتا الطرفين 1 و2 على التوالي حيث: Δu = u2 − u1
للمقاصرة نفس وحدات الكتلة (كجم حسب نظام الوحدات الدولي)، لم يفترض سميث عنصرًا نظريًا فقط، بل افترح مثال حقيقي له، وصنع نموذج صغير لتوضيح فكرته، مقاصرة سميث تتكون من مكبس قادر على التحرك داخل وخارج اسطوانة، موصل بترس مسنن والذي يحرك عجلة داخل الاسطوانة، قد تلف هذه العجلة مع عقارب الساعة أو عكس عقارب الساعة حسب اتجاه عزم الدوران الناتج، حيث إن الطاقة اللازمة لدفع المكبس تعود عندما يتحرك المكبس في الاتجاه المعاكس، ومن ثم فإن الجهاز يخزن الطاقة بدلًا تبديدها تماما مثل الكتلة، بيد أن الكتلة الفعلية لهذا النموذج يجب أن تكون صغيرة جدًا، (مثاليًا، بلا كتلة). وبهذا يمتلك هذا النموذج طرفين يتحركان بسرعتين مختلفتين، كما أنه يخرن الطاقة مثل الكتلة.[23]
وجد سميث تطبيقًا عمليًا للمقاصرة في سباق فورمولا 1، وهو ما عُرف بـالمثبط-جيه (بالإنجليزية: J-damper)، والذي استُخدم كبديل للمثبط ذي الكتلة المُضبطة (وهو محظور حاليًا) كجزء من مكبح السيارة، وقد استخدم لأول مرة سرًا من قبل ماكلارين في عام 2005 بالتعاون مع سميث، ويُعتقد أنه سيتم استخدامه على نطاق واسع في المستقبل. كذلك اقترح سميث استخدام المقاصرة للحد من اهتزاز الآلات.[24]
الرنَّان
يُمثل الرنان الميكانيكي بكتلة M ومطاوعة Cm في المجال الميكانيكي، ويُمثل في المجال الكهربي بدائرة رنان محث L ومكثف C تتكون من الحث والسعة. إذا كان لدينا كتلة ومطاوعة مثاليتين فسوف تكوّنان رنّانًا ميكانيكيًا مثلما يحدث في المجال الكهربي مع المحث والمكثف المثاليين، لكن في الواقع من الصعب الحصول على قيمة مثالية لأي من المكونات سواء الميكانيكية أو الكهربية، فلا يوجد مكثف محض ولا مطاوعة محضة، فالنابض مثلا يحتوي على مطاوعة وعلى كتلة صغيرة، والكتلة تحتوي بالأساس على كتلة وعلى مطاوعة صغيرة، ولكن يتم نظريًا فرض وجود مكونات مثالية لنتمكن من تمثيلها وتحليلها. الرنان الميكانيكي هو أهم مكون للمرشحات الميكانيكية.[25]
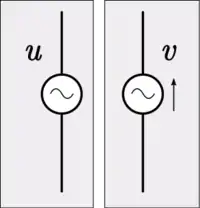
المُولِّدات
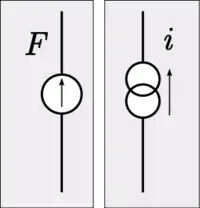
يتم تمثيل مصدر التيار الكهربي الثابت 'I' في تمثيل المعاوقة بمصدر القوة الميكانيكية الثابتة 'F'، أما مصدر الجهد الكهربي الثابت "V" فيتم تمثيله بمصدر السرعة الثابتة، بالرغم من أن مصدر الجهد الكهربي بمثابة القوة التي تدفع التيار الكهربي في المجال الكهربي، والتيار الكهربي يُعبّر عن سرعة تدفق الشحنات الكهربية، ولكن تمثيل القبولية لا يعتمد على مقدار التشابه بين المجالين ولكن يرغب فقط في الحفاظ على طوبولوجيا النظام الميكانيكي.[29]
من الأمثلة العملية على مصادر القوة الميكانيكية الثابتة النابض ثابت القوة (بالإنجليزية: constant-force spring)، وهو يماثل مصدر التيار الكهربي المثالي. ومن الأمثلة العملية على مصدر السرعة الثابتة الآلات ذات الحمل الحفيف، مثل محرك كهربي، يقود سير في مصنع، وهو يماثل مصدر الجهد الكهربي المثالي مثل بطارية كهربية تظل تعطي جهدًا ثابتًا لحمل أكبر بكثير من مقاومتها الداخلية.[26]
محولات الطاقة
تتطلب الأنظمة الكهروميكانيكية استخدام المبدلات أو محولات الطاقة للتحويل بين المجالين الكهربي والميكانيكي، حيث تستخدم أسلوب الشبكات ثنائية المنفذ (بالإنجليزية: two-port networks)، وتُوصف هؤلاء بمعادلتين وأربع متغيرات مجهولة يمكن كتابتها على شكل مصفوفة ثنائية، ويُعبَّر عن قيمة المجاهيل الأربعة بوحدة القبولية (سيمنز أو مقلوب أوم):
- على سبيل المثال: المتغير من الجانب الكهربي، والعكس مع المتغير حيث يعبر عن القبولية من الجانب الكهربي عندما تكون القوة المؤثرة على الجانب الميكانيكي بصفر، أما المتغيران الآخران و فيعبران عن موصلية النقل من الاتجاهين الأمامي والعكسي.[30]
المحولات
يمكن تمثيل المحول الكهربي بآلة ميكانيكية بسيطة مثل البكرة أو الرافعة، حيث القوة الواقعة على الحمل قد تكون أكبر أو أصغر من القوة الداخلة اعتمادًا على ما يُسمى بالميزة الميكانيكية للآلة، إن كانت قيتمها أكبر أو أصغر من الواحد. تماثل الميزة الميكانيكية في تمثيل القبولية بمعكوس النسبة بين عدد لفات طرفي المحول، فإن كانت الميزة الميكانيكية للآلة أقل تُمثَّل بمحول رافع للجهد، وإن كانت أكبر تُمثَّل بمُحول خافض للجهد.[31]
معادلات القدرة والطاقة
| الكهربائية الكمية | المعادلة الكهربية | التمثيل الميكانيكي | المعادلة الميكانيكية |
|---|---|---|---|
| الطاقة الموردة | الطاقة الموردة | ||
| القدرة الموردة | القدرة الموردة | ||
| القدرة المُبددة في المقاومة | القدرة المُبددة في المُثبّط[12] | ||
| الطاقة المُخزَّنة في المحث | طاقة الوضع المُخزَّنة في النابض[2] | ||
| الطاقة المُخزَّنة في المكثف | الطاقة الحركية لتحريك كتلة[2] |
أمثلة
دائرة رنين بسيطة
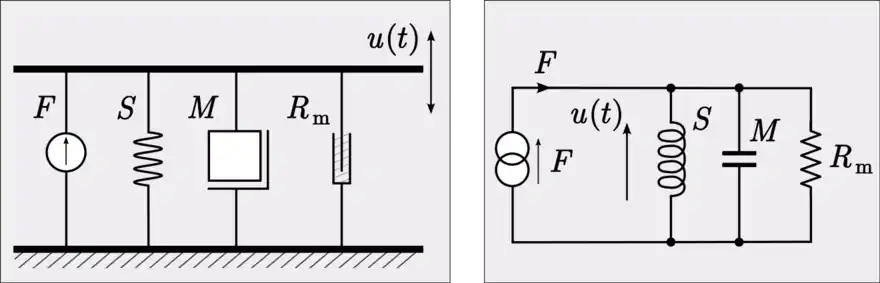
يوضح الشكل دائرة رنين ميكانيكية بسيطة من كتلة M موصلة على التوازي مع نباض S ومقاومة ميكانيكية Rm، وتُمثل باستخدام تمثيل القبولية بدائرة رنين توافقي مكونة من مقاومة ومحث ومكثف على التوازي، يحتوي كلا النظامين على نفس تردد الرنين.[32]
المزايا والعيوب
الميزة الرئيسية في تمثيل القبولية بالمقارنة بتمثيل المعاوقة هو أنه يحافظ على طوبولوجيا النظام الميكانيكي. حيث إنّ العناصر الموصلة على التوالي في النظام الميكانيكي تُمثل بعناصر موصلة على التوالي في النظام الكهربي، والموصلة على التوازي تُمثل كذلك بعناصر موصلة على التوازي، على عكس تمثيل المعاوقة.[33]
أما العيب الرئيسي في تمثيل القبولية هو أنه لا تحافظ على على التماثل بين المعاوقة الكهربائية والميكانيكية، فتُمثَّل المعاوقة الميكانيكية بالقبولية الكهربائية، وتُمثَّل المقاومة الميكانيكية بالموصلية الكهربائية، والقوة لا تماثل فرق الجهد بالرغم من أن المولد الكهربي غالبًا ما يُسمَّى بالقوة الدافعة الكهربائية، مما يجعل تمثيل القبولية أقل منطقية من تمثيل المعاوقة.
التطبيقات
يستخدم تمثيل القبولية على نطاق واسع لوضع نموذج لسلوك المرشحات الميكانيكية، حيث إنّ هذه المرشحات مصممة لاستخدامها في الدوائر الإلكترونية، لكنها تعمل بالكامل بطريقة ميكانيكية، وتستخدم المبدلات عند مداخل ومخارج المُرشحات للتحويل بين المجالين الكهربي والميكانيكي.[34]
ومن التطبيقات الأخرى الشائعة، استخدامه في مجال المعدات السمعية مثل مكبرات الصوت، حيث تتكون مكبرات الصوت من مبدلات وأجزاء ميكانيكية متحركة، كما أن الموجات الصوتية هي نفسها موجات ميكانيكية من تذبذبات جزيئات الموائع.[35]
هوامش
- Firestone 1933، صفحة 249–267
- Talbot-Smith 2013، صفحة 1.86
- Pierce 19989، صفحة 321
- Pusey 1996، صفحة 547
- Busch-Vishniac 1999، صفحة 19-20
- Findeisen 2000، صفحة 26
- Kleiner 2013، صفحة 69-70
- Busch-Vishniac 1999، صفحة 18-20
- Eargle 2003، صفحة 5
- Fahy & Gardonio 2007، صفحة 71
- Busch-Vishniac 1999، صفحة 19
- Eargle 2003، صفحة 4
- Kleiner 2013، صفحة 71
- Atkins & Escudier 2013، صفحة 216
- Kleiner 2013، صفحة 73
- Smith 2002، صفحة 1651
- Kleiner 2013، صفحة 73-74
- Kleiner 2013، صفحة 74
- Kleiner 2013، صفحة 72-73
- Busch-Vishniac 1999، صفحة 20
- Smith 2002، صفحة 1649
- Smith 2002، صفحة 1649–1650
- Smith 2002، صفحة 1650–1651
- Smith 2002، صفحة 1661
- Taylor & Huang 1997، صفحة 377–383
- Kleiner 2013، صفحة 77
- Beranek & Mellow 2012، صفحة 70
- Kleiner 2013، صفحة 76
- Kleiner 2013، صفحة 76-77
- Debnath & Roy 1987، صفحة 566–567
- Kleiner 2013، صفحة 74-76
- Eargle 2003، صفحة 4-5
- Busch-Vishniac 1999، صفحة 20-21
- Carr 2002، صفحة 170–171
- Eargle 2003، صفحة 5-8
مراجع
- Atkins & Escudier, Atkins, Tony; Escudier, Marcel (2013). A Dictionary of Mechanical Engineering. Oxford University Press. ISBN 0199587434. الوسيط
|CitationClass=تم تجاهله (مساعدة)CS1 maint: ref=harv (link) صيانة CS1: تجاهل خطأ ردمك (link) - Beranek & Mellow, Beranek, Leo Leroy; Mellow, Tim J. (2012). Acoustics: Sound Fields and Transducers. Academic Press. ISBN 0123914213. الوسيط
|CitationClass=تم تجاهله (مساعدة)CS1 maint: ref=harv (link) صيانة CS1: تجاهل خطأ ردمك (link) - Busch-Vishniac, Ilene J. (1999). Electromechanical Sensors and Actuators. Springer Science & Business Media. ISBN 038798495X. الوسيط
|CitationClass=تم تجاهله (مساعدة)CS1 maint: ref=harv (link) صيانة CS1: تجاهل خطأ ردمك (link) - Carr, Joseph J. (2002). RF Components and Circuits. Newnes. ISBN 0-7506-4844-9. الوسيط
|CitationClass=تم تجاهله (مساعدة)CS1 maint: ref=harv (link) صيانة CS1: تجاهل خطأ ردمك (link) - Debnath & Roy, Debnath, M. C.; Roy, T. (1987). ransfer scattering matrix of non-uniform surface acoustic wave transducers, vol. 10, iss. 3, pp.563–581. International Journal of Mathematics and Mathematical Sciences. مؤرشف من الأصل في 24 نوفمبر 2018. الوسيط
|CitationClass=تم تجاهله (مساعدة)CS1 maint: ref=harv (link) - Eargle, John (2003). Loudspeaker Handbook. Kluwer Academic Publishers. ISBN 1402075847. الوسيط
|CitationClass=تم تجاهله (مساعدة)CS1 maint: ref=harv (link) صيانة CS1: تجاهل خطأ ردمك (link) - Fahy & Gardonio, Fahy, Frank J.; Gardonio, Paolo (2007). Sound and Structural Vibration: Radiation, Transmission and Response. Academic Press. ISBN 0080471102. الوسيط
|CitationClass=تم تجاهله (مساعدة)CS1 maint: ref=harv (link) صيانة CS1: تجاهل خطأ ردمك (link) - Findeisen, Dietmar (2000). System Dynamics and Mechanical Vibrations. Springer. ISBN 3540671447. الوسيط
|CitationClass=تم تجاهله (مساعدة)CS1 maint: ref=harv (link) صيانة CS1: تجاهل خطأ ردمك (link) - Firestone, Floyd (1933). A new analogy between mechanical and electrical system elements, vol. 3, pp.249–267. The Journal of the Acoustical Society of America. الوسيط
|CitationClass=تم تجاهله (مساعدة)CS1 maint: ref=harv (link) - Kleiner, Mendel (2013). Electroacoustics. CRC Press. ISBN 1439836183. الوسيط
|CitationClass=تم تجاهله (مساعدة)CS1 maint: ref=harv (link) صيانة CS1: تجاهل خطأ ردمك (link) - Pierce, Allan D. (1989). Acoustics: an Introduction to its Physical Principles and Applications. Acoustical Society of America. ISBN 0883186128. الوسيط
|CitationClass=تم تجاهله (مساعدة)CS1 maint: ref=harv (link) صيانة CS1: تجاهل خطأ ردمك (link) - Pusey, Henry C. (1996). 50 years of shock and vibration technology. Shock and Vibration Information Analysis Center, Booz-Allen & Hamilton, Inc. ISBN 0964694026. الوسيط
|CitationClass=تم تجاهله (مساعدة)CS1 maint: ref=harv (link) صيانة CS1: تجاهل خطأ ردمك (link) - Smith, Malcolm C. (2002). Synthesis of mechanical networks: the inerter, vol. 47, iss. 10, pp.1648–1662. IEEE Transactions on Automatic Control. مؤرشف من الأصل في 10 أغسطس 2014. الوسيط
|CitationClass=تم تجاهله (مساعدة)CS1 maint: ref=harv (link) - Talbot-Smith, Michael (2013). Audio Engineer's Reference Book. Taylor & Francis. ISBN 1136119736. الوسيط
|CitationClass=تم تجاهله (مساعدة)CS1 maint: ref=harv (link) صيانة CS1: تجاهل خطأ ردمك (link) - Taylor & Huang, Taylor, John; Huang, Qiuting (1997). CRC Handbook of Electrical Filters. CRC Press. ISBN 0849389518. الوسيط
|CitationClass=تم تجاهله (مساعدة)CS1 maint: ref=harv (link) صيانة CS1: تجاهل خطأ ردمك (link) - De Groote, Steven, "J-dampers in Formula One", F1 Technical, 27 September 2008.
- Hähnle, W., "Die Darstellung elektromechanischer Gebilde durch rein elektrische Schaltbilder", Wissenschaftliche Veröffentlichungen aus dem Siemens-Konzern, vol. 1, iss. 11, pp. 1–23, 1932.
- Trent, Horace M., "Isomorphisms between oriented linear graphs and lumped physical systems", The Journal of the Acoustical Society of America, vol. 27, pp. 500–527, 1955.
- بوابة هندسة تطبيقية
- بوابة إلكترونيات
- بوابة كهرباء