فائدة ميكانيكية

مثال على رافعة

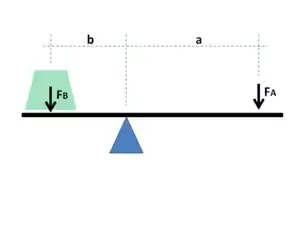
العتلة أو الرافعة هي قضيب متحرك يستطيع الدوران حول مركز دوران مثبت أو متوضع على نقطة ثابتة منه. تعمل العتلة بتطبيق قوى على مسافات مختلفة من المركز أو المُرتكَز (محور الارتكاز). يحدد موقع نقطة الارتكاز نوع العتلة. عندما تستطيع العتلة الدوران باستمرار تعمل كعتلة من النوع الثاني، ترسم حركة طرف العتلة مداراً ثابتاً يمكن فيه تبادل الطاقة الميكانيكية. (ابحث عن الكرنك اليدوي أو المرفاع اليدوي كمثال).

يُستخدم هذا النوع من العتلات الدورانية بشكل واسع في الزمن المعاصر؛ ابحث عن عتلة النوع الثاني (الدورانية)؛ ابحث عن المسننات أو السيور أو محركات النقل بالاحتكاك (القيادة بالاحتكاك أو المحرك الاحتكاكي) المستخدمة في آليات نقل القدرة الميكانيكية. من الشائع تطبيق الفائدة الميكانيكية بشكل «مطويّ» باستخدام أكثر من مسنن واحد (مجموعة مسننات). في مجموعة مسننات كهذه، تُستعمل المسننات ذات الأقطار الأصغر والفائدة الميكانيكية الذاتية الأقل. لتحقيق الفائدة من الفائدة الميكانيكية للمنظومات غير المطوية؛ من الضروري استخدام عتلة دورانية ذات «طول حقيقي» (أي ذات قضيب مستقيم). انظر، أيضاً، إدخال الفائدة الميكانيكية في تصميم أنواع معينة من المحركات الكهربائية. أحد التصاميم هو «المحرك عديم المسفرات ذو الدوار الخارجي» فعند دوران العتلة حول محور التمركز، تتحرك النقاط الأبعد عن هذا المحور بسرعة أكبر من النقاط الأقرب إليه. الاستطاعة الداخلة والخارجة من العتلة هي نفسها، وهكذا يجب أن تبقى نفسها بالحسابات. الاستطاعة (أو القدرة) هي جداء القوة بالسرعة، لذا يجب أن تكون القوى المطبقة على نقاط أبعد عن المحور أقل من القوى المطبقة على النقاط الأقرب إليه.

إذا كانت أ وب هي المسافات من المحور إلى النقاط (${\displaystyle a}$) و (${\displaystyle b}$) وإذا كانت القوة ${\displaystyle F_{A}}$ المطبقة على (${\displaystyle A}$) هي الدخل والقوة ${\displaystyle F_{B}}$ المطبقة على (${\displaystyle B}$) هي الخرج، تُعطى  نسبة السرع للنقاط (${\displaystyle A}$) و (${\displaystyle B}$) بالمقدار ${\displaystyle a/b}$ وتُعطى نسبة قوة الخرج إلى قوة الدخل بالعلاقة:

$${\displaystyle MA={\frac {F_{b}}{F_{a}}}={\frac {a}{b}}.}$$

تمثل هذه العلاقة قانون العتلة (أو الرافعة) وقد برهن عليه أرخميدس باستخدام المنطق الهندسي.[3] ويظهر القانون أنه إذا كانت المسافة (${\displaystyle a}$) من محور الارتكاز إلى مكان تطبيق قوة الدخل (النقطة ${\displaystyle A}$) أكبر من المسافة (${\displaystyle b}$) من محور الارتكاز إلى مكان تطبيق قوة الخرج (النقطة ${\displaystyle B}$)، فإن العتلة تضخم قوة الدخل. وبالعكس إذا كانت المسافة من محور الارتكاز إلى قوة الدخل أقل منها إلى قوة الخرج، فإن العتلة تقوم بتخفيض قوة الدخل. إدراكاً لما يتضمنه هذا القانون من قدرات وما ينتج عنه من استخدامات عملية نُسب إلى أرخميدس الاقتباس الشهير «أعطني مكاناً لأقف فيه وبواسطة العتلة سأستطيع تحريك العالم».[4]

استخدام السرعة في التحليل الستاتيكي (أو السكوني أو التوازني) لعتلة هو تطبيق لمبدأ الشغل الافتراضي.

يمثل شرط تساوي استطاعة الدخل لميكانيزم مثالي مع استطاعة الخرج طريقة بسيطة لحساب الفائدة الميكانيكية من نسبة سرع الدخل والخرج للجملة الميكانيكية (أو المنظومة الميكانيكية).

تساوي استطاعة الدخل لسلسلة مسننات بعزم ${\displaystyle T_{A}}$ مطبق على المسنن القائد الذي يدور بسرعة زاويّة ${\displaystyle \omega _{A}}$ بالعلاقة ${\displaystyle P=T_{A}{\displaystyle \omega _{A}}}$.

لأن تدفق الاستطاعة ثابت، يجب على العزم ${\displaystyle T_{B}}$ والسرعة الزاوية ${\displaystyle \omega _{B}}$ لمسنن الخرج أن يحققا العلاقة:

${\displaystyle P=T_{A}\omega _{A}=T_{B}\omega _{B},\!}$

وبالتالي تعطينا:

${\displaystyle MA={\frac {T_{B}}{T_{A}}}={\frac {\omega _{A}}{\omega _{B}}}.}$

أي أنه ولأجل ميكانيزم مثالي فإن نسبة سرعة الدخول إلى سرعة الخروج تساوي إلى الفائدة الميكانيكية للجملة. هذا ينطبق على كل المنظومات الميكانيكية من الروبوتات إلى الوصلات الميكانيكية.

تُصمم أسنان المسننات بحيث يكون عدد الأسنان على المسنن متناسباً مع قطر دائرة الخطوة، وبحيث تتدحرج دائرتا الخطوة لكل زوج مسننات متعشقة مع بعضهما دون انزلاق. يمكن حساب نسبة السرع لزوج المسننات المتعشقة من نسبة قطري دائرتي الخطوة ومن نسبة عدد الأسنان لكل مسنن، أي النسبة المسننية.

ترسان (مسننان) متعشقان ينقلان الحركة الدورانية.

سرعة نقطة التماس بين دائرتي الخطوة ${\displaystyle v}$ هي نفسها لكلا المسننين وتُعطى بالعلاقة:

${\displaystyle v=r_{A}\omega _{A}=r_{B}\omega _{B},\!}$

حيث يمثل ${\displaystyle A}$ نصف قطر مسنن الدخل ${\displaystyle r_{A}}$ ويتعشق مع مسنن الخرج ${\displaystyle B}$ ذي نصف القطر ${\displaystyle r_{B}}$؛ ومنه:

${\displaystyle {\frac {\omega _{A}}{\omega _{B}}}={\frac {r_{B}}{r_{A}}}={\frac {N_{B}}{N_{A}}}.}$

حيث ${\displaystyle N_{A}}$ هو عدد أسنان مسنن الدخل و${\displaystyle N_{B}}$ عدد أسنان مسنن الخرج.

يُعطى الكسب الميكانيكي لزوج المسننات المتعشقة الذي يملك فيه مسنن الدخل ${\displaystyle N_{A}}$ أسنان ومسنن الخرج ${\displaystyle N_{B}}$ أسنان بالعلاقة:

${\displaystyle MA={\frac {r_{B}}{r_{A}}}={\frac {N_{B}}{N_{A}}}.}$

ينتج عن ذلك أنه إذا كان عدد أسنان مسنن الخرج ${\displaystyle G_{B}}$  أكبر من عدد أسنان مسنن الدخل ${\displaystyle G_{A}}$، تضخم المجموعة المسننية عزم الدخل. وبالعكس، إذا كان عدد أسنان مسنن الخرج أقل من عدد أسنان مسنن الدخل، تخفض المجموعة المسننية عزم الدخل.

إذا كان مسنن خرج مجموعة مسننية يدور أبطأ من مسنن الدخل، تدعى المجموعة المسننية باسم مخفض السرعة (مضاعف القوة). في هذه الحالة، ولأن مسنن الخرج يجب أن يمتلك أسنانًا أكثر من مسنن الدخل، فإن مخفض السرعة سيضخم عزم الدخل.

تُصمم الميكانيزمات المكونة من نجمتين مسننيتين موصولتين بسلسلة، أو طارتين موصولتين بسير بحيث توفر فائدة ميكانيكية محدداً في أنظمة نقل القدرة (الاستطاعة).

سرعة السير أو السلسلة ${\displaystyle v}$ هي نفسها عند نقاط التماس مع الطارتين أو النجمتين المسننيتين:

${\displaystyle v=r_{A}\omega _{A}=r_{B}\omega _{B},\!}$

إذ تتعشق نجمة الدخل المسننية أو طارة الدخل ${\displaystyle A}$ مع السلسلة أو السير عند نصف قطر الخطوة ${\displaystyle r_{A}}$ وتتعشق نجمة الخرج المسننية أو طارة الخرج ${\displaystyle B}$ عند نصف القطر ${\displaystyle r_{B}}$ ومنه:

${\displaystyle {\frac {\omega _{A}}{\omega _{B}}}={\frac {r_{B}}{r_{A}}}={\frac {N_{B}}{N_{A}}}.}$

حيث ${\displaystyle N_{A}}$ هو عدد أسنان نجمة الدخل المسننية و ${\displaystyle N_{B}}$ عدد أسنان نجمة الخرج المسننية. في حالة السيور الناقلة المسننة، يمكن استخدام عدد أسنان النجمة المسننية. في السيور الناقلة الاحتكاكية يجب استخدام نصفي قطري دائرتي الخطوة لكل من طارتي الدخل والخرج.

تُعطى الفائدة الميكانيكية لجملة قيادة بالسلاسل أو السيور الناقلة ذات نجمة دخل مسننية عدد أسنانها ${\displaystyle N_{A}}$ ونجمة خرج مسننية عدد أسنانها ${\displaystyle N_{B}}$ بالعلاقة:

${\displaystyle MA={\frac {T_{B}}{T_{A}}}={\frac {N_{B}}{N_{A}}}.}$

تُعطى الفائدة الميكانيكية لجملة السيور الاحتكاكية بالعلاقة:

${\displaystyle MA={\frac {T_{B}}{T_{A}}}={\frac {r_{B}}{r_{A}}}.}$

تُبدد السلاسل والسيور الناقلة الاستطاعة بالاحتكاك والاهتراء والامتطاط الناتجين عن الشد ما يعني أن استطاعة الخرج أقل فعلياً من استطاعة الدخل، هذا يعني أن الفائدة الميكانيكية للجمل الحقيقية سيكون أقل من الفائدة الاسمية المحسوب لأجل ميكانيزم مثالي. يمكن للسلسلة أو السير فقدان ما يصل إلى 5 بالمئة من استطاعة المنظومة عبر الحرارة الناتجة عن الاحتكاك والتشوه والاهتراء، وفي هذه الحالة يكون مردود نظام القيادة 95%.

• بوابة هندسة ميكانيكية