هرم (هندسة)
في علم الهندسة الرياضية، الهرم هو متعدد السطوح يتم تشكيله من خلال توصيل رؤوس مضلع قاعدتة بنقطة لا تقع في نفس مستوى قاعدة الهرم تسمى قمة الهرم، ويشكل كل ضلع من أضلاع قاعدة الهرم مع قمة الهرم مثلث، وتسمى المثلثات المكونة للبناء الهرمي الغلاف الجانبي للهرم. وتسمى المضلعات التي يبنى منها الهرم وجوهاً. وبتعريف آخر الهرم : هو متعدد سطوح يبنى من غلاف جانبى كله مثلثات ذات رأس مشترك، ومن قاعدة هي مضلع. ويمكن أيضاً اعتبار الهرم مجسم مخروطى ولكن قاعدة مضلعة.
| هرم | |
|---|---|
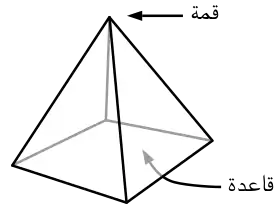 هرم رباعى هرم رباعى | |
| ترميز كونواي لمتعدد السطوح | Yn |
| الوجوه | n مثلثات، 1 n-مضلع |
| الأضلاع | 2n |
| الرؤوس | n + 1 |
| رمز وايثوف | |
| رمز شليفلي | ( ) v {n} |
| مجموعة التناظر | Cnv, [1,n], (*nn), order 2n |
| مجموعة التناوب | Cn, [1,n+], (nn), order n |
| تبادل متعدد سطوح | ذاتي |
| خصائص | محدب |
ويحدد اسم كل هرم حسب شكل قاعدته، فالهرم الذي قاعدتة مثلث يسمي هرماً ثلاثياً، والهرم الذي قاعدتة شكل رباعى يسمي هرماً رباعياً، والهرم الذي قاعدتة شكل خماسى يسمي هرماً خماسياً. وعندما لا تكون قاعدة الهرم محددة، يفترض عادة أنها قاعدة مربعة (هرم رباعى).
والهرم المكون من قاعدة ذات عدد (n) من الأضلاع سيكون له عدد (n+1) من الرؤوس، وعدد (n+1) من الوجوه، وعدد (2n) من الحواف. جميع الأهرامات هي مجسمات ذاتية التبادل.
إذا كانت قاعدة الهرم هي مضلع منتظم وقمتة تقع مباشرة فوق مركز المضلع، فالهرم ذو عدد (n)-سطوح سيكون له تماثل Cnv.
إذا كانت حواف الهرم (أو أي شكل محدب متعدد السطوح) مماسة لسطح كرة بحيث يقع متوسط نقاط التماس عند مركز الكرة، يطلق عليه الهرم المعياري أو التقليدى، وهو يشكل نصف متعدد السطوح المبادل للمكعب.
الأهرامات هي فئة فرعية من متعدد السطوح شبه المنشوري.
مسميات
- تسمى المثلثات الجانبية الأوجه الجانبية أو الغلاف الجانبي.
- تسمى المستقيمات التي يلتقي عندها كل وجهين جانبيين الأحرف الجانبية أو الحواف الجانبية.
- تسمى النقطة التي تلتقي عنها الأحرف الجانبية قمة الهرم.
- يسمى الهرم الثلاثي رباعي الوجوه.
تصنيفات
تصنف الأهرامات بحسب شكل القاعدة فيقال هرم ثلاثي، هرم رباعي ... إلخ . ويمكنك أن تقول الهرم الثلاثي أو المثلث وكليهما بنفس المعنى، أو الهرم المربع أو الرباعي وهما بنفس المعنى .
الهرم المنتظم
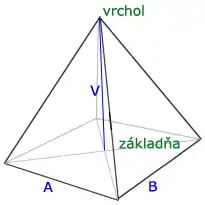
يقال عن الهرم أنه هرم منتظم إذا كانت قاعدته مضلع منتظم ، ومركزه هو موقع العمود الساقط من قمة الهرم على قاعدته. وتكون الأحرف الجانبية للهرم المنتظم متساوية في الطول والأوجه الجانبية متطابقة ومتساوية الساقين. و تكون ارتفاعات الأوجه المرسومة من قمة الهرم على أضلاع المضلع ("الارتفاعات الجانبية") متساوية في الطول. ويكون ارتفاع الهرم هو الارتفاع المرسوم من قمة الهرم ويلتقى مع القاعدة في المركز الهندسى. ويكون المركز الهندسى هو مركز الدائرة التي تمر برؤوس المضلع أو تمس أضلاعه من الداخل.
الأهرامات ذات الوجوه المنتظمة
الهرم الثلاثي أو المثلث الذي تكون قاعدته ووجوهه الجانبية الثلاثة هي عبارة عن مثلث متساوي الأضلاع يصبح رباعي الوجوه المنتظم (بالإنجليزية: regular tetrahedron)، وهو أحد المجسمات الأفلاطونية. أما حالة التماثل الأدنى للهرم الثلاثي - وهي C3v - فتكون فيها قاعدته عبارة عن مثلث متساوي الأضلاع، وغلافة الجانبى مكون من 3 مثلثات متساوية الساقين ومتطابقة. ويمكن أيضاً للأهرامات المربعة والخماسية أن تتألف من وجوه جانبية منتظمه (ذات شكل مضلع منتظم محدب)، وفي هذه الحالة تندرج تحت تعريف مجسمات جونسون.
- أشكال الأهرامات
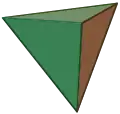
| هرم ثلاثى رباعي الوجوه المنتظم |
هرم مربع | هرم خماسي | هرم سداسى |
|---|---|---|---|
 |
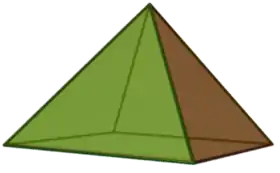 |
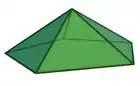 |
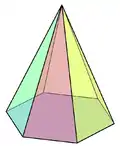 |
الأهرامات النجمية
إذا اخذت قاعدة الهرم شكل مضلع نجمي منتظم يسمى هرماً نجمياً.[1] على سبيل المثال، هرم النجم الخماسى قاعدته نجمة خماسية وله خمسة جوانب تقاطع مثلثية.
الهرم الناقص
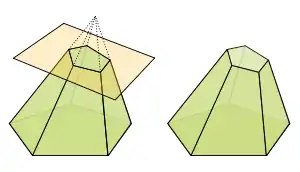
إذا قطع هرم بمستو يوازي القاعدة فإن الجزء الواقع بين المقطع والقاعدة يسمى هرما ناقصا .
قوانين متعلقة بالأهرامات
- عدد الأوجه الجانبية = عدد أضلاع القاعدة .
- عدد الأحرف الجانبية = عدد رؤوس القاعدة .
ارتفاع الهرم = هو طول القطعة المستقيمة الموصل من رأس الهرم إلى قاعدته عاموديا .
مساحة الأوجه الجانبية للهرم القائم
- إذا كان محيط القاعدة هو P و ارتفاع الوجه الجانبي هو h فإن :
- مساحة الأوجه الجانبية للهرم القائم =
مساحة الأوجه الجانبية للهرم الناقص القائم
- إذا كان P هو مجموع محيطي القاعدتين، و h هو ارتفاع الوجه الجانبي، فإن :
- مساحة الأوجه الجانبية للهرم الناقص القائم =
مساحة مقطع مشابه لقاعدة الهرم وموازي لها
- إذا كان B هو مساحة القاعدة، و h هو ارتفاع الهرم، و d هو بعد المقطع عن الرأس فإن :
- مساحة المقطع =
الحجم
حجم أي هرم = , حيث : B مساحة القاعدة و h ارتفاع الهرم.
حجم الهرم الناقص
- إذا كان h هو ارتفاع الهرم و B1 مساحة القاعدة الأولى و B2 مساحة القاعدة الثانية، فإن :
- حجم الهرم الناقص =
انظر أيضا
المصادر
- كتاب الرياضيات للصف الثالث ثانوي الصف الدراسي الثاني، طبعة 1431-1432 هـ، المملكة العربية السعودية
- Wenninger, Magnus J. (1974), Polyhedron Models, Cambridge University Press, صفحة 50, ISBN 978-0-521-09859-5, مؤرشف من الأصل في 25 يناير 2020 الوسيط
|CitationClass=تم تجاهله (مساعدة); الوسيط|separator=تم تجاهله (مساعدة)CS1 maint: ref=harv (link).
- بوابة رياضيات
- بوابة هندسة رياضية