متعدد شعب

الشكل 1: النظم البيانية الأربعة كل منها تربط جزءًا من الدائرة إلى فترة مفتوحة، ومعًا يغطون الدائرة بأكملها.

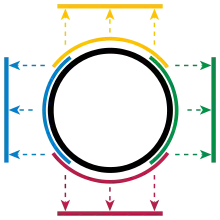
غير الخط، تعتبر الدائرة أبسط مثال على متعدد شعب. تتجاهل الطوبولوجيا الانحناء، ولذلك فإن قطعة صغيرة من الدائرة تُعامل تمامًا كما تُعامل قطعة صغيرة من خط. على سبيل المثال، انظر إلى الجزء العلوي من دائرة الوحدة، حيث الإحداثية y موجبة (القوس الأصفر في الشكل 1).  أي نقطة في هذا القوس يمكن التعبير عنها بإحداثيتها  x. لذلك، الإسقاط على الإحداثيّ الأول يمثّل دالة مستمرّة وتقابلية من القوس العلوي للفترة المفتوحة (-1، 1):

${\displaystyle \chi _{\mathrm {top} }(x,y)=x.\,}$

دوال كهذه مع المناطق المفتوحة التي يدلّون عليها تسمى نظمًا إحداثية.  بشكل مماثل، هناك نظم إحداثية للأقواس الأيسر  (أزرق) والأسفل (أحمر) والأيمن (أخضر) من الدائرة:

${\displaystyle \chi _{\mathrm {bottom} }(x,y)=x}$

${\displaystyle \chi _{\mathrm {left} }(x,y)=y}$

${\displaystyle \chi _{\mathrm {right} }(x,y)=y.}$

معًا، تغطي جميع هذه النظم البيانية الدائرة ومجموعة هذه النظم تسمى أطلسًا.

النظام البياني العلوي والأيمن يتداخلان، حيث تقاطعهم يقع في ربع الدائرة حيث كلا الإحداثيين x وy موجبان. النظامان χtop و  χright كلاهما يدلّان هذا المقطع إلى الفترة (0,1). إذًا، بالإمكان إنشاء دالة T من الفترة (0,1) لنفسها، والتي تستخدم معاكس دالّة النظام العلوي للوصول للدائرة ومن ثم العودة للفترة عن طريق دالّة النظام الأيمن. ليكن a أي عدد في (0,1). لدينا أن:

${\displaystyle {\begin{aligned}T(a)&=\chi _{\mathrm {right} }\left(\chi _{\mathrm {top} }^{-1}\left[a\right]\right)\\&=\chi _{\mathrm {right} }\left(a,{\sqrt {1-a^{2}}}\right)\\&={\sqrt {1-a^{2}}}\end{aligned}}}$

تسمى هذه الدالة دالة انتقالية.

شكل 2: نظام بياني لمتعدد شعب الدائرة مبني على الميل، يغطي جميع نقط الدائرة سوى نقطة واحدة (الزرقاء).

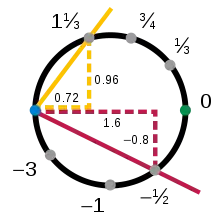
النظم البيانية العلوية والسفلية واليمنى واليسرى توضّح أن الدائرة متعدد شعب، ولكنها لا تكوّن الأطلس الوحيد للدائرة. لا يجب أن تكون النظم البيانية إسقاطات هندسية، وعدد النظم هو مسألة اختيار. انظر لدوال النظم:

${\displaystyle \chi _{\mathrm {minus} }(x,y)=s={\frac {y}{1+x}}}$

و

${\displaystyle \chi _{\mathrm {plus} }(x,y)=t={\frac {y}{1-x}}{}}$

هنا، s هو ميل الخط الذي يمر بالنقطة (x,y) ونقطة المحور الثابتة (−1, 0)، وبالمثل t هو الميل ولكن بنقطة المحور (+1, 0). الدالة العكسية من s إلى (x, y) تعطى من خلال

${\displaystyle {\begin{aligned}x&={\frac {1-s^{2}}{1+s^{2}}}\\y&={\frac {2s}{1+s^{2}}}\end{aligned}}}$

من السهل تأكيد بأن x2 + y2 = 1 لجميع قيم الميل s. هذان النظامان يوفّران أطلسًا آخر للدائرة، حيث

${\displaystyle t={\frac {1}{s}}}$

كل من النظم يحذف نقطة واحدة، إما (−1, 0) لـs أو (+1, 0) لـt. من الممكن إثبات أنه لا يمكن تغطية كل الدائرة بنظام بياني واحد.

من أشهر الأمثلة لمتعدد الشعب هي زمر لاي، وهي عبارة عن متعدد شعب ناعم (قابل للتفاضل لانهائياً)، ولديها ايضا بنية الزمرة. مثلاً، تعد الزمرة المتعامدة الخاصة ${\displaystyle SO(n,\mathbb {R} )}$ متعدد شعب حيث يتم اعتبار المصفوفات ${\displaystyle A\in \mathbb {R^{n\times n}} }$ كنقاط في الفضاء ${\displaystyle \mathbb {R^{n^{2}}} }$ وإثبات خصائص متعدد الشعب بإستخدام المبرهنة عبر الدوال الضمنية. [4]