نظام عد ثنائي

نظام العد الثنائي أو النظام الثنائي (بالإنجليزية: Binary Numeral System)‏ هو نظام عد ذو رقم أساس 2، يستخدم لتمثيل القيم العددية باستخدام رمزين، عادة ما يكونان 0 و1. كما يمكن استخدام أي رمزين أو حالتين مثل 0 و1 أو صح /خطأ أو تشغيل /إطفاء. ظام العد الثنائي مستخدم عملياً في كل الحواسب الحديثة بسبب سهولة تنفيذه مباشرةً في البوابات المنطقية والإلكترونيات الرقمية.

جزء من سلسلة مقالات حول
أنظمة العد

بوابة رياضيات
تمثيل الأعداد من -8 إلى +8 في نظام العد الثنائي بصيغ مختلفة
كلمة Wikipedia ممثلة بنظام العد الثنائي

ويسمى العدد في هذا النظام عدد ثنائي.[1]

التمثيل

عادة ما تمثل الأرقام الثنائية باستخدام 1 و0. ولكن يجب توضيح أنها ثنائية فالعدد 101 هو مئة وواحد في نظام العد العشري، ولكن بالتمثيل الثنائي فإنه يساوي العدد 5. لاحظ أن لفظ الرقم الثنائي يتم بلفظ كل خانه مثل 101 يتم لفظها واحد صفر واحد وليس مائة وواحد فهذا خطأ. كثيرًا ما يحصل التباس بين النظام العشري والثنائي عند عامة الناس، ونتيجة لذلك فإن هناك بعض الطرائف التي تطلق مثل (هناك 10 أنواع من الناس، نوع يفهم النظام الثنائي ونوع آخر لا يفهمه). حيث 10 تمثل رقم ثنائي يعادل 2.

يمكن كتابة الرقم 101 على شكل 10110 أو 1012 للتمييز بين أنظمة العد المستخدمة، فالرقم الأول يستخدم النظام العشري أما الثاني فهو يستخدم النظام الثنائي. يسمى الرقم الذي في الأسفل برقم الأساس، ويقرأ الرقم الذي يستخدم هذا الشكل للتعبير عنه: مئة وواحد للأساس 10 أو واحد صفر واحد للأساس 2.

ويمكن تمييز نظام العد الثنائي بإضافة رموز، سواء قبل العدد (بالإنجليزية: prefixed)‏ أو بعده (بالإنجليزية: postfixed)‏. ويرمز للنظام الثنائي بالرمز b أو bin (اختصارا لـ binary، أي ثنائي).

  • 10101 binary
  • 1010b (بي b تشير إلى أن العدد بالنظام الثنائي، وتلك الطريقة تسمى طريقة Intel)
  • 100101B (السابقة بي B تشير إلى أن العدد بالنظام الثنائي)
  • bin 100101 (البين bin تشير إلى أن العدد بالنظام الثنائي)
  • 1001012 (2 صغيرة مكتوبة أسفل العدد تشير على أنه نظام ثنائي)
  • %100101 (سابقة % تشير إلى النظام الثنائي، وتسمى طريقة موتورولا [2][3])

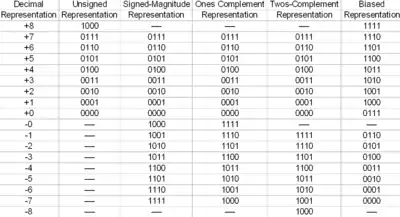
تمثيل الأعداد السالبة

تعامل الأعداد السالبة في نظام العد الثنائي بنفس الطريقة التي تعامل بها الأعداد السالبة في النظام العشري (فمثلا إضافة عدد موجب إلى عدد سالب يطرح العدد الأصغر بالقيمة المطلقة من العدد الأكبر وتعطى إشارة العدد الأكبر للناتج).

للتمييز بين الأعداد الصحيحة الموجبة والسالبة الممثلة بـ ن من الخانات الثنائية يمكن حجز الخانة الأكثر أهمية (بالإنجليزية: MSB أو Most Significant Bit)‏ لتمثيل الإشارة.

مثال: عدد ثنائي مكون من سبع خانات ثنائية (ن = 7 بت)

  • العدد موجب (MSB = 0)، مثل: 0110110
  • العدد سالب (MSB = 1)، مثل: 1110110

الرقم بالخط العريض يشير إلى الخانة الأكثر أهمية (MSB).

العلاقة مع نظام العد العشري

نظام العد الثنائي هو نظام عد يتشابه مع نظام العد العشري الشائع بأنه يستخدم الخانات ويختلف عنه بأنه ينتقل من خانة إلى أخرى كل رقمين وليس كل عشرة أرقام. وذلك يعني أن كل خانة في النظام الثنائي تحمل قيمة من اثنتين لا من عشرة، وعادة ما تستخدم القيمتان 1 و0 للتعبير عن الأعداد بالنظام الثنائي.

الأعداد بالثنائي
النظام العشري النظام الثنائي
1 1
2 10
3 11
4 100
5 101
6 110
7 111
8 1000
9 1001
10 1010
11 1011
12 1100
هذا العداد يبين كيفية العد بالنظام الثنائي من 0 إلى 31

تقوم الحواسيب بالحسابات بالأعداد الثنائية فقط، كما أنها تحول الأوامر إلى أعداد ثنائية؛ وكل عملها يتم بنظام العد الثنائي.

التحويل من النظام الثنائي إلى العشري

في النظام العشري يستخدم أساس عشري لتحديد الخانات، فمثلاً الرقم 452 هو 400+50+2 أي:

  • 2*010 +
  • 5*110 +
  • 4*210

نفس المفهوم يطبق على النظام الثنائي فالخانة الأولى من اليمين تساوي العدد مضروباً في 02 أي 1 والخانة الثانية تساوي العدد مضروباً في 12 أي 2 والخانة الثالثة تساوي العدد مضروباً في 22 أي 4... وهكذا. أمثلة:

  • الرقم 10 بالنظام الثنائي يساوي 0*1+1*2=2 بالنظام العشري
  • الرقم 11 يساوي 1*1+1*2=3 بالنظام العشري
  • الرقم 101 يساوي 1*1+0*2+1*4=5 بالنظام العشري
  • الرقم 100101 يساوي 1*1+0*2+1*4+0*8+0*16+1*32=37 بالنظام العشري أو
    • 1*02=1 +
    • 0*12=0 +
    • 1*22=4 +
    • 0*32=0 +
    • 0*42=0 +
    • 1*52=32
    • المجموع 37

طريقة القسمة المتتالية

يستخدم للجزء الطبيعي من العدد وذلك بتقسيم العدد بشكل متكرر على 2 ونأخذ الباقي الذي هو الرقم المحوَّل إليه ونتوقف. أما بالنسبة للجزء العشري من العدد فيتم بضرب الجزء العشري ب2 وأخذ العدد الصحيح ووضعه ثم الضرب مجدداً دون رقم صحيح (أي الجزء الصحيح في كل مرة يحول إلى 0 بعد أخذ قيمته) ويتوقف عند الوصول إلى قيمة 1.00

المبادلات والتجميع بـ 2

طريقة تستعمل بالنسبة للأعداد الصغيرة جدا، وهي خاصة بالأطفال، حيث يتم رسم مجموعة عدد عناصرها هو العدد العشري، ويتم تجميع كل عنصرين وتبديلهما بعنصر جديد مغاير، والباقي هو الرتبة الأولى على اليمين للتمثيل الثنائي، وتعاد نفس العملية بالنسبة للمجموعة الجديدة. وتنتهي العملية عند الحصول على مجموعة تضم عنصرا واحدا.

انظر أيضاً

مراجع
  1. المعجم الطبي الموحد نسخة محفوظة 27 أغسطس 2017 على موقع واي باك مشين.
  2. Küveler, Gerd; Schwoch, Dietrich (2013) [1996]. Arbeitsbuch Informatik - eine praxisorientierte Einführung in die Datenverarbeitung mit Projektaufgabe (باللغة الألمانية). Vieweg-Verlag, reprint: Springer-Verlag. doi:10.1007/978-3-322-92907-5. ISBN 978-3-528-04952-2. 9783322929075. مؤرشف من الأصل في 8 أبريل 2019. اطلع عليه بتاريخ 05 أغسطس 2015. الوسيط |CitationClass= تم تجاهله (مساعدة)
  3. Küveler, Gerd; Schwoch, Dietrich (2007-10-04). Informatik für Ingenieure und Naturwissenschaftler: PC- und Mikrocomputertechnik, Rechnernetze (باللغة الألمانية). 2 (الطبعة 5). Vieweg, reprint: Springer-Verlag. ISBN 3834891916. 9783834891914. مؤرشف من الأصل في 8 أبريل 2019. اطلع عليه بتاريخ 05 أغسطس 2015. الوسيط |CitationClass= تم تجاهله (مساعدة)

    وصلات خارجية
    في كومنز صور وملفات عن: نظام عد ثنائي
    • بوابة نظرية الأعداد
    • بوابة منطق
    • بوابة رياضيات
    • بوابة برمجة الحاسوب
    • بوابة تقنية المعلومات
    • بوابة علم الحاسوب
    This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.