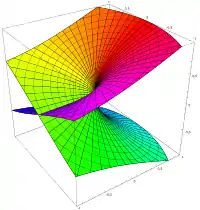
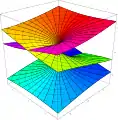
سطح ريمان

في الرياضيات، وخصوصًا في التحليل العقدي، سطح ريمان (بالإنجليزية: Riemann surface)‏، تعني متعدد الشغب المعقد (complex manifold)أحادي البعد.[1][2][3] وقد اكتشف برنارد ريمان تلك السطوح، ولذا سميت باسمه. من الممكن أن نعتبر سطوح ريمان "صورة مشوهة" للـمستوى العقدي، فمحليًا بجانب كل نقطة تبدو سطوح ريمان وكأنها بقع من المستوى العقدي، ولكن قد تكون الـطوبولوجيا العالمية مختلفة قليلاً عن ذلك. فعلى سبيل المثال، قد تبدو وكأنها كرة أو طارة (رياضيات) أو بضع ورقات ملصوقة ببعضها البعض.

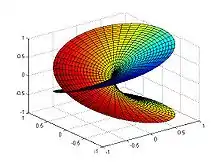
أسطح ريمان للدالةƒ(z) = √z. يمثل المحوران الأفقيان الأجزاء الحقيقية والخيالية للدالة z، بينما تمثل المحاور الرأسية الجزء الحقيقي من z√ لإيجاد الجزء الخيالي من z√ قم بتدوير الخريطة 180° حول المحاور الرأسية.

إن النقطة الرئيسية والهامة في سطوح ريمان هي إمكانية تحديد الدوال تامة الشكل بينها وتعتبر سطوح ريمان الآن بيئة مناسبة لدراسة السلوك العام لتلك الدوال، وخصوصًا الدوال متعددة القيم (مثل الجذر التربيعي وغيره من الدوال الجبرية أو اللوغاريتم.

إن كل سطح من سطوح ريمان هو متعدد شعب تحليلي حقيقي ثنائي الأبعاد (أي سطح)، ولكنه يحتوي على بنية أكثر (وخصوصًا البنية المعقدة)، والتي تعد هامة جدًا في الحصول على تعريف دقيق للدوال تامة الشكل. يمكن تحويل متعدد الشعب الحقيقي ثنائي الأبعاد إلى سطح ريمان (بالعديد من الطرق غير المتكافئة) فقط إذا كان قابلاً للتوجيه (orientable) وواقعًا في الفضاء المتري "metrizable". ولذا، تعتبر الكرة والطارة أبنية معقدة، على عكس شريط موبيوس وزجاجة كلاين ومستوى الإسقاط.

إن الحقائق الهندسية الموجودة عن سطوح ريمان تعتبر "لطيفة" إلى حد ما، وتولد الدافع لتعميمها على المنحنيات الأخرى، ومتعدد الشعب، وغيرها. وتعد مبرهنة ريمان-روخ خير مثال على ذلك التأثير.

معرض صور

انظر أيضًا
  • Dessin d'enfant
  • نظريات متعلقة بسطوح ريمان
  • تخطيط مجموعة الفئة
    • نظرية التفريع
    • نظرية تلقائية الشكل لهرويتز
    • نظرية الهوية لسطوح ريمان
    • مبرهنة ريمان-روخ
    • صيغة ريمان-هرويتز

مراجع
  1. "معلومات عن سطح ريمان على موقع idref.fr". idref.fr. مؤرشف من الأصل في 3 يونيو 2019. الوسيط |CitationClass= تم تجاهله (مساعدة)
  2. "معلومات عن سطح ريمان على موقع id.worldcat.org". id.worldcat.org. مؤرشف من الأصل في 08 ديسمبر 2019. الوسيط |CitationClass= تم تجاهله (مساعدة)
  3. "معلومات عن سطح ريمان على موقع datos.bne.es". datos.bne.es. مؤرشف من الأصل في 08 ديسمبر 2019. الوسيط |CitationClass= تم تجاهله (مساعدة)
    • Farkas, Hershel M.; Kra, Irwin (1980), Riemann Surfaces (الطبعة 2nd), Berlin, New York: Springer-Verlag, ISBN 978-0-387-90465-8 الوسيط |CitationClass= تم تجاهله (مساعدة); الوسيط |separator= تم تجاهله (مساعدة)CS1 maint: ref=harv (link)
    • Pablo Arés Gastesi, Riemann Surfaces Book.
    • Hartshorne, Robin (1977), Algebraic Geometry, Berlin, New York: Springer-Verlag, ISBN 978-0-387-90244-9, MR = 0463157 0463157, OCLC 13348052 الوسيط |CitationClass= تم تجاهله (مساعدة); الوسيط |separator= تم تجاهله (مساعدة)CS1 maint: ref=harv (link), esp. chapter IV.
    • Jost, Jürgen (2006), Compact Riemann Surfaces, Berlin, New York: Springer-Verlag, صفحات 208–219, ISBN 978-3-540-33065-3 الوسيط |CitationClass= تم تجاهله (مساعدة); الوسيط |separator= تم تجاهله (مساعدة)CS1 maint: ref=harv (link)
    • Papadopoulos, Athanase, المحرر (2007), Handbook of Teichmüller theory. Vol. I, 11, European Mathematical Society (EMS), Zürich, doi:10.4171/029, ISBN 978-3-03719-029-6, MR = 2284826 2284826 الوسيط |CitationClass= تم تجاهله (مساعدة); الوسيط |separator= تم تجاهله (مساعدة)CS1 maint: ref=harv (link)
    • Papadopoulos, Athanase, المحرر (2009), Handbook of Teichmüller theory. Vol. II, 13, European Mathematical Society (EMS), Zürich, doi:10.4171/055, ISBN 978-3-03719-055-5, MR = 2524085 2524085 الوسيط |CitationClass= تم تجاهله (مساعدة); الوسيط |separator= تم تجاهله (مساعدة)CS1 maint: ref=harv (link)
    • Papadopoulos, Athanase, المحرر (2012), Handbook of Teichmüller theory. Vol. III, 19, European Mathematical Society (EMS), Zürich, doi:10.4171/103, ISBN 978-3-03719-103-3 الوسيط |CitationClass= تم تجاهله (مساعدة); الوسيط |separator= تم تجاهله (مساعدة)CS1 maint: ref=harv (link)
    • Siegel, Carl Ludwig (1955), "Meromorphe Funktionen auf kompakten analytischen Mannigfaltigkeiten", Nachrichten der Akademie der Wissenschaften in Göttingen. II. Mathematisch-Physikalische Klasse, 1955, صفحات 71–77, ISSN 0065-5295, MR = 0074061 0074061 الوسيط |CitationClass= تم تجاهله (مساعدة); الوسيط |separator= تم تجاهله (مساعدة)CS1 maint: ref=harv (link)
    • Weyl, Hermann (2009) [1913], The concept of a Riemann surface (الطبعة 3rd), New York: Dover Publications, ISBN 978-0-486-47004-7, MR = 0069903 0069903 الوسيط |CitationClass= تم تجاهله (مساعدة); الوسيط |separator= تم تجاهله (مساعدة)CS1 maint: ref=harv (link)

    وصلات خارجية
    في كومنز صور وملفات عن: سطح ريمان
    • بوابة هندسة رياضية
    This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.