بعد
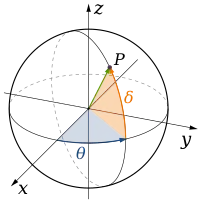
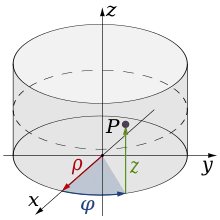
البُعد في الفيزياء والرياضيات يعرف لمكان أو لجسم بالحد الأدنى للإحداثيات اللازمة لتحديد أي نقطة في داخله.[1][2] وهذه الخطوط لها بعدا واحدا لأن إحداثي واحد فقط هو المطلوب لتحديد النقطة عليه (على سبيل المثال، النقطة عند العدد 5 على خط الأعداد). للسطوح مثل المستوى أو سطح الأسطوانة أو الكرة لها بعدين لأنه لابد من وجود إحداثيين لتحديد نقطة عليه (على سبيل المثال، لتحديد موقع نقطة على سطح كرة نحتاج إلى خط العرض و خط الطول لتلك النقطة). داخل المكعب أو الأسطوانة أو الكرة فإن الأبعاد تكون ثلاثية لأن المطلوب ثلاثة إحداثيات لتحديد نقطة ضمن هذا المكان.
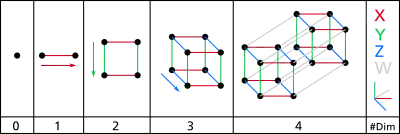 يعرض الرسم البياني أول أربعة أبعاد مكانية.1-D: نقطتين A و B يمكن توصيل خط، لإعطاء قطعة مستقيمة جديدة تسمى AB.2-D: قطعتين مستقيمتين موازييتين AB و CD ويمكن توصيلهما لتكوين مربع، مع زوايا معلمة ABCD.3-D: مربعين متوازييين ABCD و EFGH يمكن توصيلهما لتكوين مكعب، مع زوايا معلمة ABCDEFGH.4-D: مكعبين متوازييين ABCDEFGH و IJKLMNOP ويمكن توصيلهما لتكوين مكعب فائق رباعي الأبعاد، مع زوايا معلمة ABCDEFGHIJKLMNOP. |
لمعانٍ أخرى، انظر بعد (توضيح).
في الفيزياء
مراجع
- "Curious About Astronomy". Curious.astro.cornell.edu. مؤرشف من الأصل في 24 يناير 2015. اطلع عليه بتاريخ 03 مارس 2014. الوسيط
|CitationClass=تم تجاهله (مساعدة) - "MathWorld: Dimension". Mathworld.wolfram.com. 2014-02-27. مؤرشف من الأصل في 24 أكتوبر 2018. اطلع عليه بتاريخ 03 مارس 2014. الوسيط
|CitationClass=تم تجاهله (مساعدة)
- بوابة رياضيات
- بوابة هندسة رياضية
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.


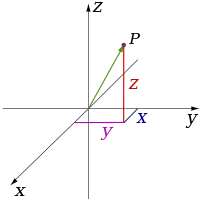
.svg.png.webp)
