اقتصار (رياضيات)

في الرياضيات، اقتصار دالة $f$ [1] هي دالة جديدة يرمز لها بـ $f\vert _{A}$ أو $f{\upharpoonright _{A}}$ ، يتم الحصول عليها من خلال اختيار أصغر مجال للدالة الأصلية $f$ .

تحتاج هذه المقالة كاملةً أو أجزاءً منها إلى تدقيق لغوي أو نحوي. فضلًا ساهم في تحسينها من خلال الصيانة اللغوية والنحوية المناسبة.

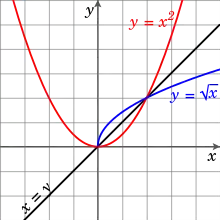
الدالة x ² ليس لديها دالة عكسية على المجال R. إذا قمنا باقتصار x ² على مجموعة الأعداد الحقيقية غير السالبة، عندها يكون لها دالة عكسية، المعروف باسم الجذر التربيعي لـx.

أمثلة

اقتصار دالة غير متباينة $f:\mathbb {R} \to \mathbb {R} ,\ x\mapsto x^{2}$ على المجال $\mathbb {R} _{+}=[0,\infty )$ هو التباين $f:\mathbb {R} _{+}\to \mathbb {R} ,\ x\mapsto x^{2}$ .
تتمثل الدالة عاملي في اقتصار الدالة غاما على مجموعة الأعداد الصحيحة الموجبة لأننا نطرح 1 من n، أي: ${\Gamma |}_{\mathbb {Z} ^{+}}\!(n)=(n-1)!$

خصائص الاقتصار

اقتصار دالة $f:X\rightarrow Y$ على المجال بأكمله $X$ يعيد إلى الدالة الأصلية، أي $f|_{X}=f$ .
اقتصار دالة مرتين هو نفسه اقتصارها مرة واحدة، أي إذا كان $A\subseteq B\subseteq \operatorname {dom} f$ ، فإنّ: $(f|_{B})|_{A}=f|_{A}$ .
إن اقتصار الدالة المحايدة المعرفة على مجموعة X على مجموعة فرعية A من X هو مجرد تباين قانوني من A إلى X.[2]
اقتصار دالة مستمرة هو عبارة عن دالة مستمرة. [3] [4]

تطبيقات

دوال عكسية

مقالة مفصلة: دالة عكسية

لكي يكون ل الدالة f دالة عكسية، يجب أن تكون تقابلية، وإذا لم تكن $f$ كذلك، يمكن تحديد دالتها العكسية عن طريق اقتصارها (تقييدها) على جزء من المجال.

على سبيل المثال، دالة $f(x)=x^{2}$ المُعرّفة عموماً على $\mathbb {R}$ ليست تقابلية لأن x ² = (- x ) ² وذلك لكل x من $\mathbb {R}$ .

ومع ذلك، تصبح الدالة $f(x)=x^{2}$ تقابلية إذا اقتصرنا على المجال $\mathbb {R} _{\geq 0}=[0,\infty [$ ، في هذه الحالة

$f^{-1}(y)={\sqrt {y}}$

ملاحظة:

(إذا كنا نود أن نقتصر على المجال $]-\infty ,0]$ ، فإن دالتها العكسية ستكون $-{\sqrt {y}}$ ) بدلاً من ذلك، ليست هناك حاجة لاقتصار المجال إذا كنا لا نريد إيجاد الدالة العكسية كونها دالة متعددة القيم.

اختيار المؤثرات

هذا القسم فارغ أو غير مكتمل، ساهم بتحريره.

الحزم

مقالة مفصلة: حزمة (رياضيات)

هذا القسم فارغ أو غير مكتمل، ساهم بتحريره.

انظر أيضا

مراجع

ترجمة و معنى restriction في قاموس المعاني. قاموس عربي انجليزي نسخة محفوظة 3 يناير 2020 على موقع واي باك مشين.
Halmos, Paul (1960). Naive Set Theory. Princeton, NJ: D. Van Nostrand. الوسيط |CitationClass= تم تجاهله (مساعدة) Reprinted by Springer-Verlag, New York, 1974. (ردمك 0-387-90092-6) (Springer-Verlag edition). Reprinted by Martino Fine Books, 2011. (ردمك 978-1-61427-131-4) (Paperback edition).
Munkres, James R. (2000). Topology (الطبعة 2nd). Upper Saddle River: Prentice Hall. ISBN 0-13-181629-2. الوسيط |CitationClass= تم تجاهله (مساعدة)
Adams, Colin Conrad; Franzosa, Robert David (2008). Introduction to Topology: Pure and Applied. Pearson Prentice Hall. ISBN 978-0-13-184869-6. الوسيط |CitationClass= تم تجاهله (مساعدة)

بوابة رياضيات
بوابة تحليل رياضي

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.

[1] ترجمة و معنى restriction في قاموس المعاني. قاموس عربي انجليزي نسخة محفوظة 3 يناير 2020 على موقع واي باك مشين.

[2] Halmos, Paul (1960). Naive Set Theory. Princeton, NJ: D. Van Nostrand. الوسيط |CitationClass= تم تجاهله (مساعدة) Reprinted by Springer-Verlag, New York, 1974. (ردمك 0-387-90092-6) (Springer-Verlag edition). Reprinted by Martino Fine Books, 2011. (ردمك 978-1-61427-131-4) (Paperback edition).

[3] Munkres, James R. (2000). Topology (الطبعة 2nd). Upper Saddle River: Prentice Hall. ISBN 0-13-181629-2. الوسيط |CitationClass= تم تجاهله (مساعدة)

[4] Adams, Colin Conrad; Franzosa, Robert David (2008). Introduction to Topology: Pure and Applied. Pearson Prentice Hall. ISBN 978-0-13-184869-6. الوسيط |CitationClass= تم تجاهله (مساعدة)