مربع لاتيني

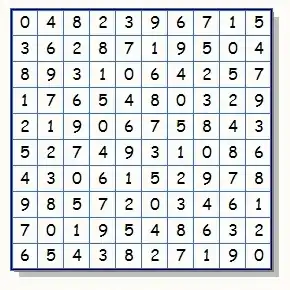
في علم التوافقيات وتصميم التجارب، المربع اللاتيني (بالإنجليزية: latin square)‏ هو مصفوفة n × n معمرة بعلامات (أرقام، أحرف،أشكال) حيث تنقسم تلك العلامات إلى أنواع عددها n. حيث تعمر كل خانة بعلامة وحيدة. ولا يتككر أي نوع من العلامات -في العمود الواحد أو في أي صف أفقي- أكثر من مرة.يمكن أن يوجد أكثر من حل للمربع اللاتيني بنفس الترتيب.[1] مثلا حيث n = 3 يوجد 12 حلا (و تشملها المصفوفات المتناظرة)، منها

مربع لاتيني ذا 10 أعمدة.

الحسابات قد الهمت ليونهارت أويلر (عالم رياضيات) المصطلح "مربع لاتيني" لأنه كان يستخدم الحروف اللاتينية (A,B,C,D...) كعلامات.[2]

عدد المربعات اللاتنية المختلفة ذا الترتيب n حيث ...n = 1,2,3,4 هي 1, 2, 12, 576, 161280, 812851200...(OEIS-A002860). وقد يصل عددها إلى قيم كبيرة مثل $\approx 7.48671\times 10^{74}$ بالنسبة للترتيب 13.[3]

السودوكو هي حالة خاصة من المربع اللاتيني.

حالات خاصة

مربع لاتيني مخفض

يسمى المربع مربعا لاتينيا متنخفضا (و يقال أيlضkا طبيعيا) إذا كانت رموز أول عمود له وأول صف له مرتبة بترتيبها الطبيعي (في هذه الحالة تكون الرموز سلسلة من الأعداد أو الحروف الألفبائية المرتبة)، مثل َA,B,C أو 1,2,3.

مثال:

${\color {Blue}\mathbf {C} }$	${\color {Blue}\mathbf {B} }$	${\color {Purple}\mathbf {A} }$
$\mathbf {A}$	$\mathbf {C}$	${\color {Red}\mathbf {B} }$
$\mathbf {B}$	$\mathbf {A}$	${\color {Red}\mathbf {C} }$

توجد فقط حالة واحدة يكون فيها المربع اللاتيني منخفضا بالنسبة إلى المصفوفات 1×1 و2×2 و3×3.

فقط ${\frac {100\%}{n!(n-1)!}}$ من المربعات اللاتنية ذات الترتيب n هي مربعات لاتينية منخفضة.

n	عدد المربعات اللاتيني المنخفضة ذا القياس n	عدد جميع المربعات اللاتنية المختلفة ذا القياس n
1	1	1
2	1	2
3	1	12
4	4	576
5	56	161280
6	9408	812851200
7	16942080	61479419904000
8	535281401856	108776032459082956800
9	377597570964258816	5524751496156892842531225600
10	7580721483160132811489280	9982437658213039871725064756920320000
11	5363937773277371298119673540771840	776966836171770144107444346734230682311065600000

انظر أيضا

المراجع

Latin Square - from Wolfram MathWorld نسخة محفوظة 11 نوفمبر 2017 على موقع واي باك مشين.
Wallis, W. D.; George, J. C. (2011), Introduction to Combinatorics, CRC Press, p. 212, ISBN 978-1-4398-0623-4. نسخة محفوظة 19 أغسطس 2014 على موقع واي باك مشين.
http://www.wolframalpha.com/input/?i=latin+squares&a=*C.latin+squares-_*MathWorld- نسخة محفوظة 19 أغسطس 2014 على موقع واي باك مشين.

في كومنز صور وملفات عن: مربع لاتيني

بوابة رياضيات
بوابة إحصاء

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.

[1] Latin Square - from Wolfram MathWorld نسخة محفوظة 11 نوفمبر 2017 على موقع واي باك مشين.

[2] Wallis, W. D.; George, J. C. (2011), Introduction to Combinatorics, CRC Press, p. 212, ISBN 978-1-4398-0623-4. نسخة محفوظة 19 أغسطس 2014 على موقع واي باك مشين.

[3] ttp://www.wolframalpha.com/input/?i=latin+squares&a=*C.latin+squares-_*MathWorld- نسخة محفوظة 19 أغسطس 2014 على موقع واي باك مشين.