مربعات دنيا

طريقة المربعات الصغرى أو الدنيا (بالإنجليزية: Least squares)‏ هي طريقة احصاء تهدف إلى تقدير خط انحدار الذي يؤدي إلى تقليل مجموع الانحرافات الرئيسية أو الأخطاء الواردة في النقاط التي تمت ملاحظتها في خط الانحدار أي يتم التقليل من مجموع مربعات الفروق بين القيم الفعلية والقيم المحسوبة.[1][2][3] ويمكن القول أيضا انها طريقة تقريب قياسية تستخدم لحل أنظمة المعادلات التي يكون فيها عدد المعادلات أكبر من عدد المتغيرات. "المربعات الدنيا" تعني بأن الحل الكلي يتجه نحو تصغير قيمة مجموع مربعات الخطأ الناتج عن حل كل معادلة.

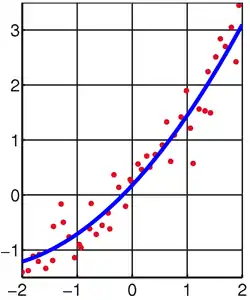
نتيجة الإسقاط الشكلي لمجموعة نقاط على دالة من الدرجة الثانية.

من أهم التطبيقات هو الإسقاط الشكلي للبيانات (data fitting). حيث أن أفضل إسقاط شكلي لمجموعة بيانات يتجه نحو تصغير مجموع مربعات الأخطاء، حيث أن الخطأ هو الفرق بين القيمة المقاسة للبيانات والقيمة المسقطة على الشكل. تم وصف مسألة المربعات الدنيا للمرة الأولى من قبل كارل غاوس حوالي عام 1794.

انظر أيضا

مراجع

"معلومات عن مربعات دنيا على موقع meshb.nlm.nih.gov". meshb.nlm.nih.gov. مؤرشف من الأصل في 8 سبتمبر 2019. الوسيط |CitationClass= تم تجاهله (مساعدة)
"معلومات عن مربعات دنيا على موقع id.ndl.go.jp". id.ndl.go.jp. مؤرشف من الأصل في 19 أبريل 2020. الوسيط |CitationClass= تم تجاهله (مساعدة)
"معلومات عن مربعات دنيا على موقع thes.bncf.firenze.sbn.it". thes.bncf.firenze.sbn.it. مؤرشف من الأصل في 31 أغسطس 2019. الوسيط |CitationClass= تم تجاهله (مساعدة)

بوابة إحصاء

في كومنز صور وملفات عن: مربعات دنيا

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.

[1] "معلومات عن مربعات دنيا على موقع meshb.nlm.nih.gov". meshb.nlm.nih.gov. مؤرشف من الأصل في 8 سبتمبر 2019. الوسيط |CitationClass= تم تجاهله (مساعدة)

[2] "معلومات عن مربعات دنيا على موقع id.ndl.go.jp". id.ndl.go.jp. مؤرشف من الأصل في 19 أبريل 2020. الوسيط |CitationClass= تم تجاهله (مساعدة)

[3] "معلومات عن مربعات دنيا على موقع thes.bncf.firenze.sbn.it". thes.bncf.firenze.sbn.it. مؤرشف من الأصل في 31 أغسطس 2019. الوسيط |CitationClass= تم تجاهله (مساعدة)