مبدأ الضرب
في التوافقيات، قاعدة الضرب أو مبدأ الضرب أو مبدأ المضاعفة هو أحد مبادئ العد الأساسية. وهي مبدأ ينص على أنه إذا كان هناك a من الطرق لفعل شيء وَ b من الطرق لفعل شيء آخر، فإن هناك a · b طريقة لفعل العملين معاً.[1][2]
أمثلة
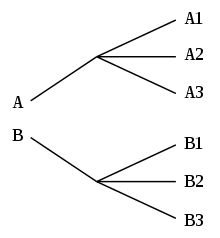
في هذا المثال، تنص القاعدة على: ضرب 3 في 2، والناتج 6.
المجموعات {A, B, C} وَ {X, Y} في هذا المثال هما مجموعات متفارقة، وهذا لا يهم في مبدأ الضرب. وكمثال آخر، عند طلبك بيتزا، فإنه يجب عليك أولاً اختيار سُمك التغطية: رقيقة أو عريضة (اختياران). ومن ثم تختار نوع التغطية: جبن، ببروني، سجق (3 اختيارات). باستخدام مبدأ الضرب، فأنت تعلم أن هناك 2×3 = 6 اختيارات ممكنة لطلب بيتزا.
التطبيقات
في نظرية المجموعات، مبدأ الضرب هذا غالباً ما يؤخذ على أنه تعريف لحاصل ضرب عدد أصلي.[1] لدينا:
حيث أن × هي عملية جداء ديكارتي. هذه المجموعات ينبغي لها أن لا تكون منتهية، وليس من الضروري وجود معاملات لانهائية في حاصل الضرب؛ انظر أيضاً عدد أصلي.
مفاهيم مرتبطة
قاعدة مبدأ الجمع هي إحدى مبادئ العد الأساسية الأخرى. والتي تنص على أنه إذا كان لدينا a عدد من طرق فعل شيء ما وَ b من الطرق لفعل شيء آخر، ونحن لا نستطيع فعل الشيئين معاً فإنه هناك a + b طريقة لفعل ذلك.
انظر أيضاً
مراجع
- Johnston, William, and Alex McAllister.
- "College Algebra Tutorial 55: Fundamental Counting Principle". مؤرشف من الأصل في 11 أكتوبر 2018. اطلع عليه بتاريخ 20 ديسمبر 2014. الوسيط
|CitationClass=تم تجاهله (مساعدة)
- بوابة رياضيات
- بوابة علوم