مبادئ العد الأساسية
مبادئ العد الأساسية أو مبادئ التركيبات أو قواعد التركيبات هي مجموعة من المبادئ أو القواعد المعروفة للعد، وهي شائعة الاستخدام.[1] قاعدة الجمع، وقاعدة الضرب، وقاعدة التضمين والإقصاء غالباً ما تستخدم لأغراض حسابية. بينما مبرهنات بيجكتف فتستخدم لإيضاح أن مجموعتين تحتوي على نفس عدد العناصر. ويستخدم مبدأ برج الحمام لتحقيق وجود شيء ما، أو يستخدم لتحديد أقصى وأدنى قيمة لعدد شيء ما في الرياضيات المتقطعة، العديد من المتطابقات التركيبية تظهر من طرق العد المتكرر أو طريقة العنصر المميز. الدالة المولدة وعلاقة الاستدعاء الذاتي هي أدوات قوية التي يمكن استخدامها للحصول على علاقات ومتتابعات، ويمكن أن تصف أو تحل أي مسألة تركيبية.
مبدأ الجمع
مبدأ الجمع هي مبدأ بديهي ينص على إنه هناك a من النتائج المحتملة لحدث (أو طريقة لفعل شيء) و b من النتائج المحتملة لحدث آخر (أو طرائق لعمل شيء آخر)، وكلا الحدثين لا يمكن أن يحصلا معاً (أو أن كلاهما لا يمكن إنجازه معاً)، فإن هناك a + b عدد من الاحتمالات الكلية للنتائج أو الأحداث (أو الطرق الكلية لعمل شيء من الأشياء). ويمكن التعبير عن ذلك رياضياتياً بقول: مجموع منطقتي مجموعتين متفارقتين يساوي منطقة اتحادهما.
قاعدة الضرب
مبدأ الضرب هي من أحد المبادئ البديهية أيضاً وتنص على أنه إذا كان هناك a من الطرق لعمل شيء ما و b من الطرق لعمل شيء آخر، إذن هناك a·b طريقة لعمل كلا العملين.
مبدأ التضمين والإقصاء
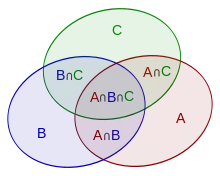
مبدأ التضمين والإقصاء يرتبط بمناطق الاشتراك لعدة مجموعات، منطقة كل مجموعة، ومنطقة كل تقاطع محتمل للمجموعات. أبسط مثال هو أنه حين توافر مجموعتين: فإن عدد عناصر اتحاد A وَ B يساوي مجموع عدد عناصر كلاً من المجموعتين منقصاً منه عدد العناصر في منطقة اتحادهما.
وبشكل عام، واستناداً لهذا المبدأ، فإنه إذا كانت A1, ..., An مجموعات منتهية، فإذن
مبرهنة بجكتف
مبرهنات بجكتف تُثبت أن مجموعتين يحتويات على نفس عدد العناصر بإيجاد الدالة التقابلية (تطابق عنصر لعنصر) من مجموعة لأخرى.
العد المتكرر
أسلوب العد المتكرر يُستعمل عند تعادل تعبيرين يمكن استعمالهما لحساب منطقة أحد المجموعات بطريقتين.
مبدأ برج الحمام
ينص مبدأ برج الحمام على أنه إذا كان هناك a من العناصر وكل عنصر سيتم وضعه في b من الصناديق، حيث أن a > b، فإنه أحد الصناديق يحتوي على أكثر من عنصر واحد. وباستخدام هذا المبدأ فإنه يمكن -على سبيل المثال- إثبات وجود بعض العناصر في مجموعة مع بعض الخصائص.
طريقة العنصر المميز
أسلوب العنصر المميز يُفرّد عنصراً من مجموعة لإثبات بعض النتائج.
الدوال المولدة
توليد الدوال يمكن اعتباره على أنه أحد أنواع كثيرات الحدود التي تكون معاملات حدودها تطابق حدود متتابعة. هذا التمثيل الجديد للمتتابعة يفتح المجال لطرق جديدة لإيجاد المتطابقات والصيغ المغلقة المتعلقة بتتابع معين. الدالة المولدة للمتتابعة an هي:
العلاقات المتكررة
العلاقة المتكررة تعبر عن كل حد من المتتابعة a في صورة حدود سابقة. العلاقات المتكررة من الممكن أن تؤدي إلى خاصية سابقة لمتتابعة، ولكن بشكل عام فإن تعبيرات الصيغ المغلقة للحدود لمتتابعة هي الأكثر شيوعاً.
مراجع
- "معلومات عن مبادئ العد الأساسية على موقع academic.microsoft.com". academic.microsoft.com. مؤرشف من الأصل في 6 أبريل 2020. الوسيط
|CitationClass=تم تجاهله (مساعدة)
- J. H. van Lint and R. M. Wilson (2001), A Course in Combinatorics (Paperback), 2nd edition, Cambridge University Press. ISBN 0-521-00601-5
- بوابة رياضيات