قائمة إسقاطات الخرائط
هذا ملخص لإسقاطات الخرائط. نظرًا لعدد إسقاطات الخرائط المحتملة غير منتهية،[1] لا يمكن أن تكون هناك قائمة شاملة.
جدول الإسقاطات
| الإسقاط | الصورة | النوع | الخصائص | المخترع | السنة | الملاحظات |
|---|---|---|---|---|---|---|
| إسقاط متساوي المستطيلات
= أسطواني متساوي المسافات = مستطيلية |
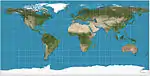 |
أسطواني | متساوي المسافات | مارينوس الصوري | ح. 120 | أبسط هندسة؛ المسافات على طول خطوط الطول محفوظة. |
| إسقاط كاسيني
= كاسيني–سولدنر |
 |
أسطواني | متساوي المسافات | سيزار-فرانسوا كاسيني | 1745 | إسقاط متساوي البعد عرضي؛ المسافات على طول خط الزوال المركزي محفوظة.
المسافات العمودية على خط الطول المركزي محفوظة. |
| إسقاط مركاتور | 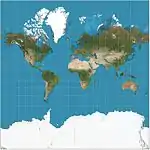 |
أسطواني | محافظ (Conformal) | جيراردوس مركاتور | 1569 | خطوط الاتجاه الثابتة مستقيمة، تساعد على الملاحة. تضخم المساحات مع خطوط العرض تصبح شديدة لدرجة أن الخريطة لا يمكنها إظهار القطبين. |
| إسقاط مركاتور للويب | 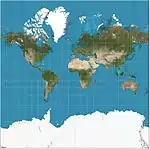 |
أسطواني | توفيقي
(Compromise) |
جوجل | 2005 | Variant of Mercator that ignores Earth's ellipticity for fast calculation, and clips latitudes to ~85.05° for square presentation. De facto standard for Web mapping applications. |
| إسقاط غاوس-كروغر= إسقاط غاوس محافظ= (ellipsoidal) transverse Mercator |  |
أسطواني | محافظ | كارل فريدريش غاوس | 1822 | This transverse, ellipsoidal form of the Mercator is finite, unlike the equatorial Mercator. Forms the basis of the Universal Transverse Mercator coordinate system. |
| إسقاط سمتي مائل لروسي | هنري روسي [الفرنسية] | 1922 | ||||
| Hotine oblique Mercator | 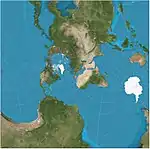 |
أسطواني | محافظ | M. Rosenmund, J. Laborde, Martin Hotine | 1903 | |
| Gall stereographic |  |
أسطواني | توفيقي | جيمس غال | 1855 | Intended to resemble the Mercator while also displaying the poles. Standard parallels at 45°N/S. |
| إسقاط ميلر
= Miller cylindrical |
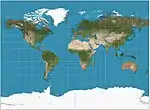 |
أسطواني | توفيقي | أوسبورن ميتلاند ميلر | 1942 | Intended to resemble the Mercator while also displaying the poles. |
| Lambert cylindrical equal-area | أسطواني | متساوي المساحات | يوهان هاينغيش لامبرت | 1772 | Standard parallel at the equator. Aspect ratio of π (3.14). Base projection of the cylindrical equal-area family. | |
| Behrmann | 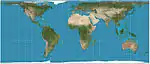 |
أسطواني | متساوي المساحات | فالتر بيرمان | 1910 | Horizontally compressed version of the Lambert equal-area. Has standard parallels at 30°N/S and an aspect ratio of 2.36. |
| Hobo–Dyer |  |
أسطواني | متساوي المساحات | Mick Dyer | 2002 | Horizontally compressed version of the Lambert equal-area. Very similar are Trystan Edwards and Smyth equal surface (= Craster rectangular) projections with standard parallels at around 37°N/S. Aspect ratio of ~2.0. |
| إسقاط غال-بيترز= Gall orthographic= Peters | 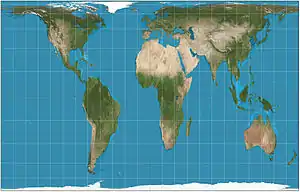 |
أسطواني | متساوي المساحات | جيمس غال | 1855 | Horizontally compressed version of the Lambert equal-area. Standard parallels at 45°N/S. Aspect ratio of ~1.6. Similar is Balthasart projection with standard parallels at 50°N/S. |
| إسقاك أسطواني مركزي |  |
أسطواني | منظوري
(Perspective) |
(غير معروف) | ح. 1850 | Practically unused in cartography because of severe polar distortion, but popular in panoramic photography, especially for architectural scenes. |
| إسقاط جيبي | 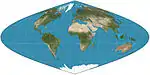 |
شبه أسطواني | متساوي المساحات والمسافات | (Several; first is unknown) | ح. 1600 | Meridians are sinusoids; parallels are equally spaced. Aspect ratio of 2:1. Distances along parallels are conserved. |
| إسقاط مولفيده | 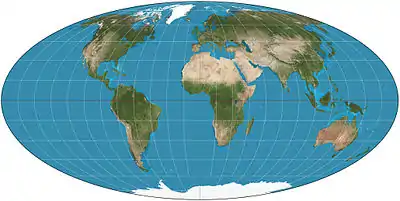 |
شبه أسطواني | متساوي المساحات | كارل مولفيده | 1805 | Meridians are ellipses. |
| Eckert II | 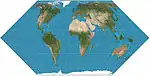 |
شبه أسطواني | متساوي المساحات | ماكس إيكرت-غرايفيندروف | 1906 | |
| Eckert IV | 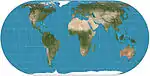 |
شبه أسطواني | متساوي المساحات | ماكس إيكرت-غرايفيندروف | 1906 | Parallels are unequal in spacing and scale; outer meridians are semicircles; other meridians are semiellipses. |
| Eckert VI | 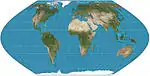 |
شبه أسطواني | متساوي المساحات | ماكس إيكرت-غرايفيندروف | 1906 | Parallels are unequal in spacing and scale; meridians are half-period sinusoids. |
| إسقاط أورتيليوس البيضوي | 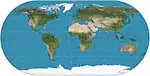 |
شبه أسطواني | توفيقي | باتيستا أنييزي | 1540 | Meridians are circular.[2] |
| Goode homolosine | 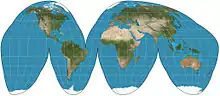 |
شبه أسطواني | متساوي المساحات | جون بول غود | 1923 | Hybrid of Sinusoidal and Mollweide projections.
Usually used in interrupted form. |
| Kavrayskiy VII | 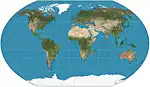 |
شبه أسطواني | توفيقي | فلاديمير كافرايسكي | 1939 | Evenly spaced parallels. Equivalent to Wagner VI horizontally compressed by a factor of . |
| Robinson | 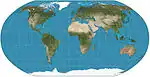 |
شبه أسطواني | توفيقي | آرثر روبنسون | 1963 | Computed by interpolation of tabulated values. Used by Rand McNally since inception and used by NGS in 1988–1998. |
| Equal Earth | 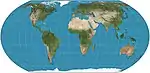 |
شبه أسطواني | متساوي المساحات | Bojan Šavrič, Tom Patterson, Bernhard Jenny | 2018 | Inspired by the Robinson projection, but retains the relative size of areas. |
| Natural Earth | 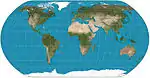 |
شبه أسطواني | توفيقي | Tom Patterson | 2011 | Computed by interpolation of tabulated values. |
| Tobler hyperelliptical |  |
شبه أسطواني | متساوي المساحات | Waldo R. Tobler | 1973 | A family of map projections that includes as special cases Mollweide projection, Collignon projection, and the various cylindrical equal-area projections. |
| Wagner VI | 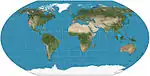 |
شبه أسطواني | توفيقي | K. H. Wagner | 1932 | Equivalent to Kavrayskiy VII vertically compressed by a factor of . |
| Collignon | شبه أسطواني | متساوي المساحات | Édouard Collignon | ح. 1865 | Depending on configuration, the projection also may map the sphere to a single diamond or a pair of squares. | |
| HEALPix |  |
شبه أسطواني | متساوي المساحات | Krzysztof M. Górski | 1997 | Hybrid of Collignon + Lambert cylindrical equal-area. |
| Boggs eumorphic | 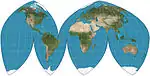 |
شبه أسطواني | متساوي المساحات | Samuel Whittemore Boggs | 1929 | The equal-area projection that results from average of sinusoidal and Mollweide y-coordinates and thereby constraining the x coordinate. |
| Craster parabolic
=Putniņš P4 |
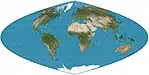 |
شبه أسطواني | متساوي المساحات | John Craster | 1929 | Meridians are parabolas. Standard parallels at 36°46′N/S; parallels are unequal in spacing and scale; 2:1 aspect. |
| McBryde–Thomas flat-pole quartic
= McBryde–Thomas #4 |
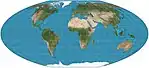 |
شبه أسطواني | متساوي المساحات | Felix W. McBryde, Paul Thomas | 1949 | Standard parallels at 33°45′N/S; parallels are unequal in spacing and scale; meridians are fourth-order curves. Distortion-free only where the standard parallels intersect the central meridian. |
| Quartic authalic | 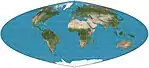 |
شبه أسطواني | متساوي المساحات | Karl Siemon
Oscar Adams |
1937
1944 |
Parallels are unequal in spacing and scale. No distortion along the equator. Meridians are fourth-order curves. |
| The Times |  |
شبه أسطواني | توفيقي | John Muir | 1965 | Standard parallels 45°N/S. Parallels based on Gall stereographic, but with curved meridians. Developed for Bartholomew Ltd., The Times Atlas. |
| Loximuthal | 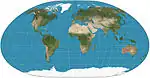 |
شبه أسطواني | توفيقي | Karl Siemon | 1935
1966 |
From the designated centre, lines of constant bearing (rhumb lines/loxodromes) are straight and have the correct length. Generally asymmetric about the equator. |
| Aitoff | 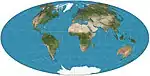 |
شبه سمتي | توفيقي | David A. Aitoff | 1889 | Stretching of modified equatorial azimuthal equidistant map. Boundary is 2:1 ellipse. Largely superseded by Hammer. |
| Hammer= Hammer–Aitoffvariations: Briesemeister; Nordic | 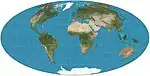 |
شبه سمتي | متساوي المساحات | Ernst Hammer | 1892 | Modified from azimuthal equal-area equatorial map. Boundary is 2:1 ellipse. Variants are oblique versions, centred on 45°N. |
| Strebe 1995 |  |
شبه سمتي | متساوي المساحات | Daniel "daan" Strebe | 1994 | Formulated by using other equal-area map projections as transformations. |
| Winkel tripel | 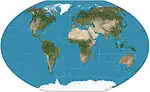 |
شبه سمتي | توفيقي | Oswald Winkel | 1921 | Arithmetic mean of the equirectangular projection and the Aitoff projection. Standard world projection for the NGS since 1998. |
| Van der Grinten |  |
أخرى | توفيقي | Alphons J. van der Grinten | 1904 | Boundary is a circle. All parallels and meridians are circular arcs. Usually clipped near 80°N/S. Standard world projection of the NGS in 1922–1988. |
| Equidistant conic= simple conic | 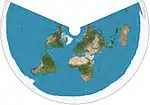 |
مخروطي | متساوي المسافات | Based on Ptolemy's 1st Projection | ح. 100 | Distances along meridians are conserved, as is distance along one or two standard parallels.[3] |
| Lambert conformal conic | 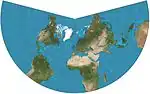 |
مخروطي | محافظ | Johann Heinrich Lambert | 1772 | Used in aviation charts. |
| Albers conic | 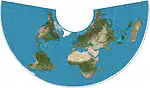 |
مخروطي | متساوي المساحات | Heinrich C. Albers | 1805 | Two standard parallels with low distortion between them. |
| Werner |  |
شبه مخروطي | متساوي المساحات والمسافات | Johannes Stabius | ح. 1500 | Parallels are equally spaced concentric circular arcs. Distances from the North Pole are correct as are the curved distances along parallels and distances along central meridian. |
| Bonne | 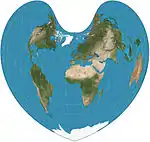 |
Pseudoconical, cordiform | متساوي المساحات | Bernardus Sylvanus | 1511 | Parallels are equally spaced concentric circular arcs and standard lines. Appearance depends on reference parallel. General case of both Werner and sinusoidal. |
| Bottomley |  |
شبه مخروطي | متساوي المساحات | Henry Bottomley | 2003 | Alternative to the Bonne projection with simpler overall shape
Parallels are elliptical arcs Appearance depends on reference parallel. |
| American polyconic | 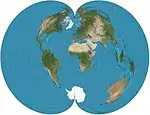 |
شبه مخروطي | توفيقي | Ferdinand Rudolph Hassler | ح. 1820 | Distances along the parallels are preserved as are distances along the central meridian. |
| Rectangular polyconic | 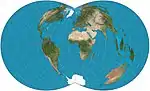 |
شبه مخروطي | توفيقي | U.S. Coast Survey | ح. 1853 | Latitude along which scale is correct can be chosen. Parallels meet meridians at right angles. |
| Latitudinally equal-differential polyconic | شبه مخروطي | توفيقي | China State Bureau of Surveying and Mapping | 1963 | Polyconic: parallels are non-concentric arcs of circles. | |
| Nicolosi globular |  |
شبه مخروطي[4] | توفيقي | Abū Rayḥān al-Bīrūnī؛ reinvented by Giovanni Battista Nicolosi, 1660.[1]:14 | ح. 1000 | |
| إسقاط سمتي متساوي المسافات=Postel=zenithal equidistant |  |
سمتي | متساوي المسافات | Abū Rayḥān al-Bīrūnī | ح. 1000 | Distances from center are conserved.
Used as the emblem of the United Nations, extending to 60° S. |
| إسقاط مزولي | 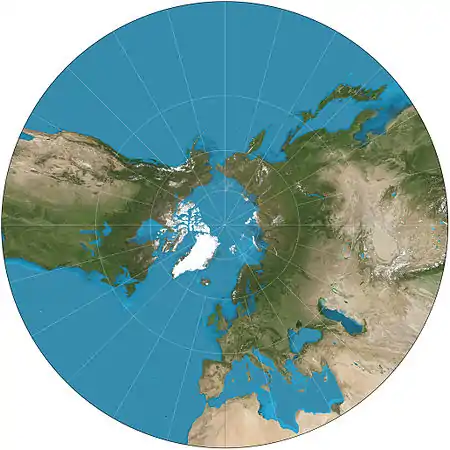 |
سمتي | مزولي (Gnomonic) | Thales (possibly) | ح. 580 BC | All great circles map to straight lines. Extreme distortion far from the center. Shows less than one hemisphere. |
| Lambert azimuthal equal-area | 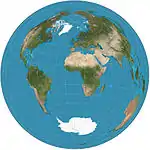 |
سمتي | متساوي المساحات | Johann Heinrich Lambert | 1772 | The straight-line distance between the central point on the map to any other point is the same as the straight-line 3D distance through the globe between the two points. |
| Stereographic | 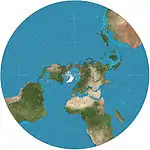 |
سمتي | محافظ | Hipparchos* | ح. 200 BC | Map is infinite in extent with outer hemisphere inflating severely, so it is often used as two hemispheres. Maps all small circles to circles, which is useful for planetary mapping to preserve the shapes of craters. |
| Orthographic |  |
سمتي | منظوري | Hipparchos* | ح. 200 BC | View from an infinite distance. |
| Vertical perspective | 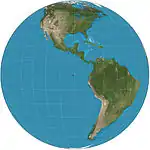 |
سمتي | منظوري | Matthias Seutter* | 1740 | View from a finite distance. Can only display less than a hemisphere. |
| Two-point equidistant | 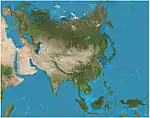 |
سمتي | متساوي المسافات | Hans Maurer | 1919 | Two "control points" can be almost arbitrarily chosen. The two straight-line distances from any point on the map to the two control points are correct. |
| Peirce quincuncial |  |
أخرى | محافظ | Charles Sanders Peirce | 1879 | Tessellates. Can be tiled continuously on a plane, with edge-crossings matching except for four singular points per tile. |
| Guyou hemisphere-in-a-square projection |  |
أخرى | محافظ | Émile Guyou | 1887 | Tessellates. |
| Adams hemisphere-in-a-square projection | 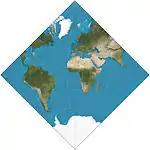 |
أخرى | محافظ | Oscar Sherman Adams | 1925 | |
| Lee conformal world on a tetrahedron |  |
إسقاط متعدد السطوح
(Polyhedral) |
محافظ | L. P. Lee | 1965 | Projects the globe onto a regular tetrahedron. Tessellates. |
| AuthaGraph projection | Link to file | متعدد السطوح | توفيقي | Hajime Narukawa | 1999 | Approximately equal-area. Tessellates. |
| Octant projection |  |
متعدد السطوح | توفيقي | Leonardo da Vinci | 1514 | Projects the globe onto eight octants (Reuleaux triangles) with no meridians and no parallels. |
| Cahill's butterfly map | 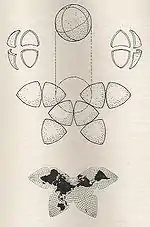 |
متعدد السطوح | توفيقي | Bernard Joseph Stanislaus Cahill | 1909 | Projects the globe onto an octahedron with symmetrical components and contiguous landmasses that may be displayed in various arrangements. |
| Cahill–Keyes projection | 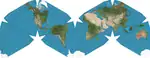 |
متعدد السطوح | توفيقي | Gene Keyes | 1975 | Projects the globe onto a truncated octahedron with symmetrical components and contiguous land masses that may be displayed in various arrangements. |
| Waterman butterfly projection |  |
متعدد السطوح | توفيقي | Steve Waterman | 1996 | Projects the globe onto a truncated octahedron with symmetrical components and contiguous land masses that may be displayed in various arrangements. |
| Quadrilateralized spherical cube | متعدد السطوح | متساوي المساحات | F. Kenneth Chan, E. M. O'Neill | 1973 | ||
| Dymaxion map |  |
متعدد السطوح | توفيقي | Buckminster Fuller | 1943 | Also known as a Fuller Projection. |
| Myriahedral projections | متعدد السطوح | متساوي المساحات | Jarke J. van Wijk | 2008 | Projects the globe onto a myriahedron: a polyhedron with a very large number of faces.[5][6] | |
| Craig retroazimuthal= Mecca | 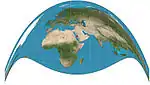 |
Retroazimuthal | توفيقي | James Ireland Craig | 1909 | |
| Hammer retroazimuthal, front hemisphere |  |
Retroazimuthal | Ernst Hammer | 1910 | ||
| Hammer retroazimuthal, back hemisphere |  |
Retroazimuthal | Ernst Hammer | 1910 | ||
| Littrow | 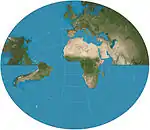 |
Retroazimuthal | محافظ | Joseph Johann Littrow | 1833 | on equatorial aspect it shows a hemisphere except for poles. |
| Armadillo | 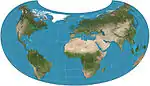 |
أخرى | توفيقي | Erwin Raisz | 1943 | |
| GS50 |  |
أخرى | محافظ | John P. Snyder | 1982 | Designed specifically to minimize distortion when used to display all 50 U.S. states. |
| Wagner VII
= Hammer-Wagner |
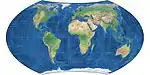 |
شبه سمتي | متساوي المساحات | K. H. Wagner | 1941 | |
| Atlantis
= Transverse Mollweide |
 |
شبه أسطواني | متساوي المساحات | John Bartholomew | 1948 | Oblique version of Mollweide |
| Bertin
= Bertin-Rivière = Bertin 1953 |
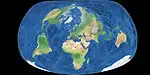 |
أخرى | توفيقي | Jacques Bertin | 1953 | Projection in which the compromise is no longer homogeneous but instead is modified for a larger deformation of the oceans, to achieve lesser deformation of the continents. Commonly used for French geopolitical maps.[7] |
مراجع
- Snyder, John P. (1993). Flattening the earth: two thousand years of map projections. دار نشر جامعة شيكاغو. صفحة 1. ISBN 0-226-76746-9. الوسيط
|CitationClass=تم تجاهله (مساعدة) - Donald Fenna (2006). Cartographic Science: A Compendium of Map Projections, with Derivations. CRC Press. صفحة 249. ISBN 978-0-8493-8169-0. مؤرشف من الأصل في 9 أغسطس 2020. الوسيط
|CitationClass=تم تجاهله (مساعدة) - Furuti, Carlos A. "Conic Projections: Equidistant Conic Projections". Archived from the original on 20 ديسمبر 2013. اطلع عليه بتاريخ 11 فبراير 2020. الوسيط
|CitationClass=تم تجاهله (مساعدة)صيانة CS1: رابط غير صالح (link) - "Nicolosi Globular projection" نسخة محفوظة 2016-04-29 على موقع واي باك مشين.
- Jarke J. van Wijk. "Unfolding the Earth: Myriahedral Projections". مؤرشف من الأصل في 20 يونيو 2020. الوسيط
|CitationClass=تم تجاهله (مساعدة) - Carlos A. Furuti. "Interrupted Maps: Myriahedral Maps". مؤرشف من الأصل في 17 يناير 2020. الوسيط
|CitationClass=تم تجاهله (مساعدة) - Rivière, Philippe (October 1, 2017). "Bertin Projection (1953)". visionscarto. مؤرشف من الأصل في 27 يناير 2020. اطلع عليه بتاريخ 27 يناير 2020. الوسيط
|CitationClass=تم تجاهله (مساعدة)
- بوابة جغرافيا
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.
