علاقة انعكاسية
في الرياضيات، علاقة انعكاسية أو علاقة عكسية (بالإنجليزية: reflexive relation) هي علاقة ثنائية على مجموعة ما، حيث كل عنصر مرتبط بنفسه في إطار هذه العلاقة. بكلمات أخرى؛ تكون العلاقة ~ انعكاسية على مجموعة S عندما يكون x ~ x صحيحاً من أجل كل عنصر x من S. أبسط مثال على هذه العلاقات هي علاقة التساوي في مجموعة الأعداد الحقيقية، بما أن كل عدد مساوى لنفسه، وتوصف المجموعة عندها بأنها تملك خاصة انعكاسية.
مصطلحات ذات صلة
العلاقة غير العكسية (بالإنجليزية: irreflexive أو anti-reflexive)، وهي علاقة ثنائية على مجموعة ما حيث لا يرتبط فيها عنصر بنفسه، كمثال علاقة "أكبر قطعا من" (x>y) في مجموعة الأعداد الحقيقية، لاحظ بأنه عندما لا تكون العلاقة عكسية فهي ليست بالضرورة غير عكسية، من الممكن تعريف علاقة ترتبط فيها بعض العناصر ببعضها. كمثال العلاقة الثنائية "حاصل ضرب x في y هو عدد زوجي"، هي عكسية على مجموعة الأعداد الزوجية، وغير عكسية على مجموعة الأعداد الفردية، وليست عكسية ولا غير عكسية على مجموعة الأعداد الطبيعية.
أمثلة
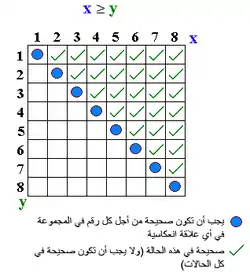
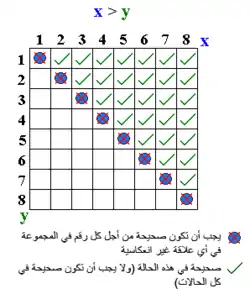
أمثلة عن علاقات انعكاسية
- "مساوي لـ" (علاقة التساوي)
- "مجموعة جزئية من"
- "قابل للقسمة على" (قابلية القسمة)
- "أكبر من أو يساوي"
- "أصغر من أو يساوي"
أمثلة عن علاقات غير انعكاسية
- "غير مساوي لـ"
- "هو عدد أولي بالنسبة لـ" (من أجل الأعداد الصحيحة أكبر من 1، بما أن 1 عدد أولي بالنسبة لنفسه)
- "أكبر من"
- "أصغر من"
عدد العلاقات العكسية
عدد العلاقات الانعكاسية في مجموعة من ن عنصر هو 2ن2−ن.[1]
| عدد العلاقات الثنائية من ن عنصر من أنواع مختلفة | ||||||||
|---|---|---|---|---|---|---|---|---|
| ن | الكل | متعدية | انعكاسية | ترتيب مسبق (preorder) | ترتيب جزئي | ترتيب مسبق كلي (total preorder) | ترتيب كلي | علاقة تكافؤ |
| 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| 1 | 2 | 2 | 1 | 1 | 1 | 1 | 1 | 1 |
| 2 | 16 | 13 | 4 | 4 | 3 | 3 | 2 | 2 |
| 3 | 512 | 171 | 64 | 29 | 19 | 13 | 6 | 5 |
| 4 | 65536 | 3994 | 4096 | 355 | 219 | 75 | 24 | 15 |
| موسوعة المتتاليات الصحيحة على الإنترنت | A002416 | A006905 | A053763 | A000798 | A001035 | A000670 | A000142 | A000110 |