صدى المغزل

يُشير مصطلح صدى المغزل في الرنين المغناطيسي إلى إعادة تركيز مغنطة المغزل بواسطة نبضة من الإشعاع الكهرومغناطيسي الرنان، [1] وهو تأثير يُستخدم في الرنين المغناطيسي النووي والتصوير بالرنين المغناطيسي.

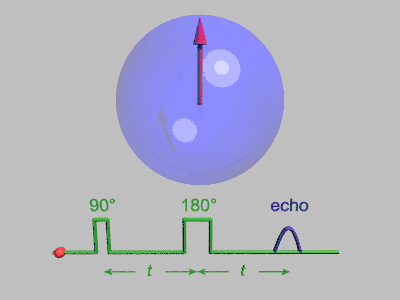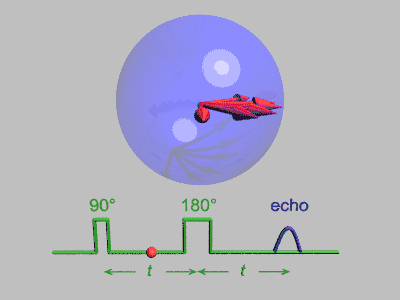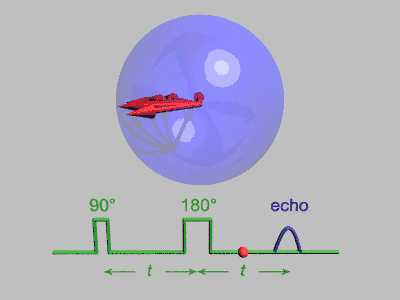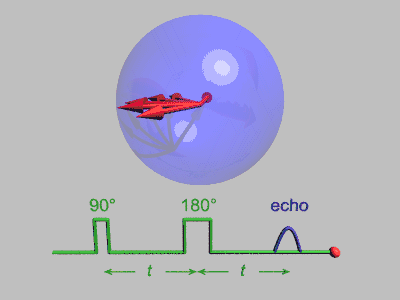
رسم متحرك لصدى المغزل يوضح استجابة المغزل (الأسهم الحمراء) في كرة بلوخ (الزرقاء) لتتابع النبضات (الأخضر)

اكتُشف أن إشارة الرنين المغناطيسي النووي الملحوظة بعد نبضة الإستثارة الابتدائية تتحلل بمرور الوقت، وذلك بسبب كل من استرخاء المغزل الذي يؤدي إلى فقدان دائم للمغنطة، والتأثيرات الغير متجانسة التي تؤدي إلى مداورة المغزل بمعدلات مختلفة، والتي يمكن إزالتها عن طريق إرسال نبضة عاكسة بزاوية 180 لعكس متجهات المغنطة،[2] وتشمل أمثلة التأثيرات غير المتجانسة تدرج المجال المغناطيسي وتوزيع الانزياح الكيميائي.

تٌعتبر ظاهرة الصدى خاصية هامة في التحليل الطيفي المتماسك، والذي يُستخدم في مجالات أخرى غير الرنين المغناطيسي، منها التحليل الطيفي بالليزر، [3] صدى المغزل النيوتروني، وقد اكتشف إروين هان عام 1950 ظاهرة الصدى في الرنين المغناطيسي النووي لأول مرة، [4] ولذلك يُشار أحيانًا إلى صدى الدوران باسم صدى هان.

مبدأ العمل

اكتشف إروين هان تأثير صدى المغزل عندما أطلق نبضتين متتاليتين بزاوية 90 درجة مفصولتين عن بعضهما بفترة زمنية قصيرة، ليلاحظ بعدها وجود إشارة (صدى)، وقد شرح إروين هان ظاهرة صدى المغزل هذه في ورقته البحثية عام 1950، [4] والتي طورها كل من كار وبورسيل الذان أشارا إلى مزايا استخدام نبضة إعادة تركيز بزاوية 180 درجة للنبضة الثانية،[5] ويمكن فهم تتابع النبضات بشكل أفضل من خلال تقسيمه إلى الخطوات التالية:

تسلسل صدى الدوران
  1. يُمثل السهم الأحمر العمودي متوسط العزم المغناطيسي للمغزل (مجموعة من المغازل)، كلها عمودية في المجال المغناطيسي العمودي وتدور على محورها الطويل، لكن هذا الرسم التوضيحي موجود في إطار مرجعي دوار حيث تكون الدورات ثابتة في المتوسط.
  2. بإرسال نبضة بزاوية 90 درجة فإن السهم يُقلب إلى المستوى الأفقي.
  3. بسبب عدم تجانس المجال المغناطيسي الموجود، وعند وقت معين، يتباطأ بعض أسهم المعزل بسبب انخفاض شدة المجال السفلي (وبالتالي تبدأ الأسهم بالتتابع التدريجي نحو الخلف) بينما يتسارع البعض الآخر بسبب قوة المجال العلوي (وتبدأ الأسهم بالتتابع التدريجي نحو الأمام)، وهذا ما يجعل الإشارة تتحلل.
  1. في هذه الخطوة يتم إرسال نبضة بزاوية 180 درجة بحيث يتقدم المغزل الأبطأ العزم الرئيسي ويلحق به المغزل السريع خلفه.
  2. تدريجيًا يلتحق المغزل السريع بالعزم الرئيسي ويعود المغزل البطيئ إلى العزم الرئيسي.
  3. تتم إعادة التركيز البؤري بالكامل في هذه الخطوة، ويمكن القياس الدقيق لصدى التوفيت الأفقي (T2) مع إزالة جميع تأثيرات التوقيت الأفقي الفعال (T2 star)، فيما تمثل عودة السهم الأحمر للاتجاه العمودي (غير موضح بالرسم) ارتخاء التوقيت الرأسي (T1).

تُستخدم العديد من التبسيطات في هذا التتابع، فلا يحدث فك للترابط الكمي، كما أن كل مغزل يصله نبضات مثالية دون أي انتشار، ويمثل الشكل التالي العملية مجتمعة:

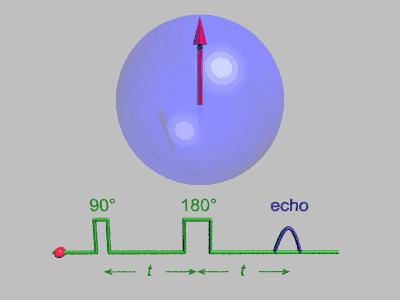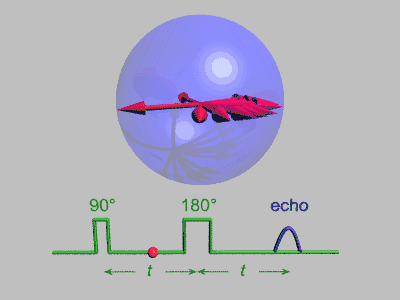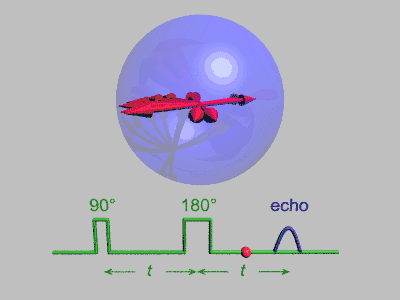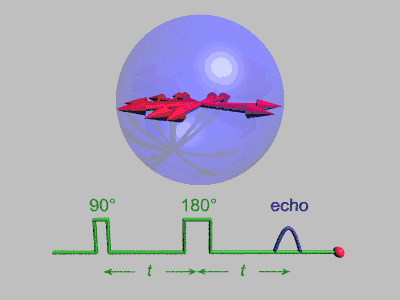
تحلل صدى المغزل

يمكن استخدام تجربة تحلل صدى المغزل لقياس وقت استرخاء المغزل، كما هو موضح في الرسم المتحرك أدناه. يتم تسجيل حجم الصدى في تباعد النبضتين. هذا يكشف عن عدم الترابط الذي لا يُعاد تركيزه بواسطة النبضة العاكسه. وفي الحالات البسيطة يتم قياس التضاؤل الأسي الذي يتم وصفه بواسطة التوقيت الأفقي (T 2).

انظر أيضًا

المراجع
  1. J. E. Tanner; E. O. Stejskal (2003). "Restricted Self-Diffusion of Protons in Colloidal Systems by the Pulsed-Gradient, Spin-Echo Method". The Journal of Chemical Physics. 49 (4): 1768. Bibcode:1968JChPh..49.1768T. doi:10.1063/1.1670306. الوسيط |CitationClass= تم تجاهله (مساعدة)
  2. Malcolm H. Levitt; Ray Freeman (1979). "NMR population inversion using a composite pulse". Journal of Magnetic Resonance. 33 (2): 473–476. Bibcode:1979JMagR..33..473L. doi:10.1016/0022-2364(79)90265-8. الوسيط |CitationClass= تم تجاهله (مساعدة)
  3. Kurnit, N. A.; Abella, I. D.; Hartmann, S. R. (1964). "Observation of a photon echo". Physical Review Letters. 13 (19): 567–568. Bibcode:1964PhRvL..13..567K. doi:10.1103/PhysRevLett.13.567. الوسيط |CitationClass= تم تجاهله (مساعدة)
  4. Hahn, E.L. (1950). "Spin echoes". Physical Review. 80 (4): 580–594. Bibcode:1950PhRv...80..580H. doi:10.1103/PhysRev.80.580. الوسيط |CitationClass= تم تجاهله (مساعدة)
  5. Carr, H. Y.; Purcell, E. M. (1954). "Effects of Diffusion on Free Precession in Nuclear Magnetic Resonance Experiments". Physical Review. 94 (3): 630–638. Bibcode:1954PhRv...94..630C. doi:10.1103/PhysRev.94.630. الوسيط |CitationClass= تم تجاهله (مساعدة)

    قراءة متعمقة
    • Ray Freeman (1999). Spin Choreography: Basic Steps in High Resolution NMR. Oxford University Press. ISBN 978-0-19-850481-8. الوسيط |CitationClass= تم تجاهله (مساعدة)

    روابط خارجية
    الرسوم المتحركة والمحاكاة
    صدى المغزل في المشاريع الشقيقة
    • بوابة الفيزياء
    This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.