شبه كروي
الكُرَوَاني[1] أو الشِبْه الكُرَوي (بالإنجليزية: Spheroid) هو سطح دوراني, يتولد عندما راسم سطحة يكون إهليلج (بما فيه الدائرة كحالة خاصة من الإهليلج) ومحور الدوران هو واحد من محاور نفس الاهليلج .[2][3][4]
 |
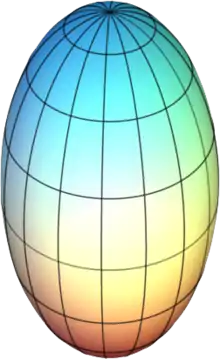 |
| شبه كروي مفلطح oblate spheroid | شبه كروي متطاول prolate spheroid |
هناك ثلاثة أنواع من الأسطح الكروية :
- شبه كروي متطاول أو ممطوط (وبخاصه بإتجاه المحور القطبي، مماثل لشكل كرة الرغبي)، إذا كان راسم السطح يكون إهليج ومحور الدوران هو المحور الأكبر لنفس الإهليلج.
- شبه كروي مفلطح (مماثل لشكل كوكب الأرض)، إذا كان الراسم إهليج والدوران يحدث حول المحور الأصغر.
- كرة، إذا كان الراسم دائرة .
المعادلات الرياضية
معادلة القطع الناقص ثلاثي المحاور المُتمركز في نقطة الأصل الذي يمتلك أنصاف المحاور «إيه» و«بي» و«سي» على طول محاور الإحداثيات الثلاث:
تُعطى معادلة السطح الكروي باعتبار أن المحور «زي» هو محور التماثل بمساواة a مع b:
نصف المحور إيه هو نصف القطر الاستوائي للسطح الكروي، وسي هي المسافة من المركز إلى القطب على طول محور التماثل. هناك حالتان ممكنتان:
- c < a: سطح كروي مُفلطح.
- c > a: سطح كروي مُتطاول.
- a = c: كرة.
الخصائص
المساحة
يتمتع السطح الكروي المُفلطح مع c < a بمساحة سطح تُعطى بالصيغة التالية:
- حيث
ينتج السطح الكروي المُفلطح عن تدوير قطع ناقص يمتلك المحور نصف الأكبر إيه والمحور نصف الأصغر سي حول المحور زي، وبالتالي يمكن تعريف a بأنه الاختلاف المركزي.[5]
يتمتع السطح الكروي المُتطاول مع c > a بمساحة سطح تُعطى بالصيغة التالية:
- حيث
ينتج السطح الكروي المُتطاول عن تدوير قطع ناقص يمتلك المحور نصف الأكبر سي والمحور نصف الأصغر إيه حول المحور زي، لذا يمكن مرة أخرى تعريف إي بأنه الاختلاف المركزي.[6]
هذه الصيغ متطابقة بمعنى أنه يمكن استخدام صيغة مساحة السطح الكروي المُفلطح لحساب مساحة السطح الكروي المُتطاول والعكس صحيح. مع ذلك، يصبح إي بعد ذلك عددًا تخيليًا ولا يمكن اعتباره اختلافًا مركزيًا بشكل مباشر. يمكن تطبيق هذه النتائج على العديد من الأشكال الأخرى باستخدام المتطابقات الرياضية القياسية والعلاقات بين معاملات القطع الناقص.
مراجع
- "LDLP - Librairie Du Liban Publishers". www.ldlp-dictionary.com. مؤرشف من الأصل في 26 يونيو 2020. اطلع عليه بتاريخ 26 يونيو 2020. الوسيط
|CitationClass=تم تجاهله (مساعدة) - John Pellerito, Joseph F Polak (2012). Introduction to Vascular Ultrasonography (الطبعة 6). Elsevier Health Sciences. ISBN 9781455737666. الوسيط
|CitationClass=تم تجاهله (مساعدة) - "Oblate Spheroid - from Wolfram MathWorld". Mathworld.wolfram.com. مؤرشف من الأصل في 24 يناير 2018. اطلع عليه بتاريخ 24 يونيو 2014. الوسيط
|CitationClass=تم تجاهله (مساعدة) - Torge, Geodesy, p.104 نسخة محفوظة 09 مايو 2016 على موقع واي باك مشين.
- A derivation of this result may be found at "Oblate Spheroid - from Wolfram MathWorld". Mathworld.wolfram.com. مؤرشف من الأصل في 18 مارس 2020. اطلع عليه بتاريخ 24 يونيو 2014. الوسيط
|CitationClass=تم تجاهله (مساعدة) - A derivation of this result may be found at "Prolate Spheroid - from Wolfram MathWorld". Mathworld.wolfram.com. 7 October 2003. مؤرشف من الأصل في 21 أكتوبر 2019. اطلع عليه بتاريخ 24 يونيو 2014. الوسيط
|CitationClass=تم تجاهله (مساعدة)
- بوابة هندسة رياضية
- بوابة الفيزياء
