شارع كارمان الدوامي
شارع كارمان الدوامي (بالإنجليزية: Karman Vortex street) هي ظاهرة في ميكانيكا الموائع وهي حدوث دوامات في مائع (الهواء أو سائل) جاري عند تعديته لجسم .[1][2] تحدث تلك الدوامات متناوبة خلف الجسم، وتسمى بشارع كارمان الدوامي نسبة إلى مكتشفها "ثيودور كارمان". اهتم كارمان بدراسة تلك الدوامات وابتكر طرق لحسابها في عام 1911 .
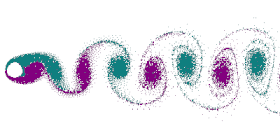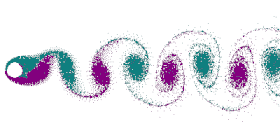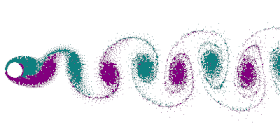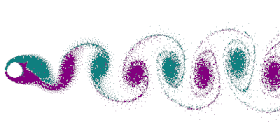
نشأة الدوامات
يتحكم في نشأة الدوامات عدد رينولدز ويرمز له بالرمز Re . وهذا العدد يعطي النسبة بين قوى القصور الذاتي وقوى اللزوجة ، ويمكن حساب عدد رينولدز عن طريق سرعة جريان الهواء أو السائل، ولزوجته، وقطر الجسم الواقف كمانع في جريان المائع . وفي الحالة البسيطة حيث يفترض أن الجسم في شكل أسطوانة، ويمر عليه المائع بسرعة معينة، فيمكن باستخدام عدد رينولدز استنتاج أشكال مختلفة للدوامات الناشئة خلف الأسطوانة .
عندما تكون سرعة المائع صغيرة أو عندما تكون لزوجة المائع عالية (مثلما لعسل النحل: Re < 4-5 )، فلا تحدث دوامات . وبزيادة السرعة تنشأ على ناحيتي الأسطوانة دوامتان متضادتا اتجاه الدوران، وتصبحان غير مستقرتان عندما يصل عدد رينولدز بين Re = 30-48 ، وتظهر حركتهما الاهتزازية الدورية . وتنفصل الدوامتين عند تردد معين يحدده عدد آخر يسمى عدد ستروهال . وبتزايد عدد رينولدز حتي يصل إلى Re = 180-200 يكون سريان المائع لا يزال جريان صفائحي.
وعندما يزيد عدد رينولدز عن ذلك ينتقل الجريان من "جريان صفائحي" إلى جريان دوامي . وعند وصول عدد رينولدز الحرج Rekrit ≈ 10.000 تكون مقاومة الجسم (المانع) أقل ما يمكن . وحتى لو وصل عدد رينولدز إلى (Re > 5 Mio)، كما يحدث أحيانا عند جريان الريح على جزر عالية في البحر فيمكن مشاهدة شارع كرمان الدوامي . ويمكن مشاهدة تلك الظاهرة خلف أبراج الاتصالات إذا كان الجو محملا بالسحب أو الغبار.
أمثلة
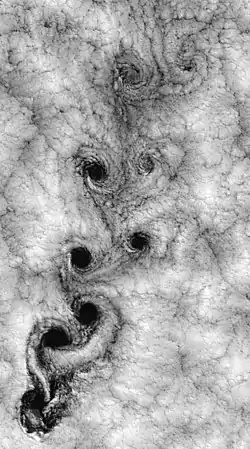

ظاهرة الدوامات وشوارع الدوامات هي ظاهرة تحدث كثيرا، ولكن تصعب مشاهدتها أحيانا. هذا لأن رؤية الرياح وجريان الهواء ليس من السهل . كذلك بالنسبة إلى دوامات الماء يصعب رؤياها بسبب شفافية الماء . ومع ذلك فيمكن بالتمعن رؤي دوامات في حوض مثلا عندما يكون الماء ساكنا ونقطعه بأحد أصابعنا . عندئذ يمكننا مشاهدة "شارع دوامات ".
وإذا استبدلنا الماء بسائل ذو لزوجة عالية مثل مخلوط ماء وجلسرين، مع إضافة لون من ألوان الأطعمة، مثل شراب الكريز أو الفرولة، عندئذ نستطيع رؤية أوتار وخيوط ملونة اللون تدور في اتجاه دوران الدوامات .
يبين الفيديو أسفله صورة متحركة مبينا نشأة دوامات في الماء عند عبورها لعائق، ونرى الدوامات تتحرك مع تيار الماء، كما نرى أن اتجاه دوران الدوامة يكون في اتجاه العائق .

يمكن حدوث شوراع كارمان الدوامية مثلا خلف جزيرة عالية أو عدة دزر عالية في البحر، ونجدها تعلو عن سطح الماء . وتظهر تلك الدوامات أثناء التصوير من الجو أو من قمر صناعي في هيئة تشكيلات صخمة من السحب . وهذا ما نراه في صورة القمر الصناعي المعروضة أعلاه إلى اليسار .
تردد الانفصال
يمكن الحصول على "تردد انفصال" دوامة (انفصال عن العائق) باستخدام عدد ستروهال . تنطبق المعادلة :
- ,
حيث:
- سرعة جريان الوسط، وليكن الماء مثلا،
- و مقاييس الجسم العائق .
يعتمد عدد ستروهال على شكل العائق وعلى عدد رينولد، وهو عدد خاص بالموائع . وبافتراض أن العائق شكله اسطواني فإن عدد رينولد الخاص به بين 0,18-0,22. وسنختار في مثالنا هنا . والبعد الهام بالنسبة لتكون الدوامات هو قطر الأسطوانة حيث تكون الأسطوانة قائمة عموديا في الماء . وبناء على ذلك ينتج هوائي سيارة ذو قطر يبلغ 4 مليمتر ويكون منصوبا على سقف سيارة تسير بسرعة 25 متر في الثانية (90 كيلومتر في الساعة) ، تنتج صوتا (موسيقى) عاليا واضحا بالتردد :
- .
ومثال آخر :
وهو تصفير خطوط الضغط العالي عند مرور الريح عليها .
ونطرا لكون العلاقة بين "تردد الانفصال " وسرعة جريان المائع هي علاقة خطية (أي تتناسب طرديا مع سرعة جريان المائع) ، فيستخدم " مقياس جريان المائع" لتعيين لزوجة المواد ذات لزوجة منخفضة .
اقرأ أيضاً
- رقم فرود
- عدد رينولد
- عدد ستروهال
- جريان صفائحي
- جريان دوامي
- قانون هاجن-بوازوي
مراجع
- "معلومات عن شارع كارمان الدوامي على موقع d-nb.info". d-nb.info. مؤرشف من الأصل في 25 يناير 2020. الوسيط
|CitationClass=تم تجاهله (مساعدة) - "معلومات عن شارع كارمان الدوامي على موقع britannica.com". britannica.com. مؤرشف من الأصل في 26 سبتمبر 2015. الوسيط
|CitationClass=تم تجاهله (مساعدة)
 صور وملفات صوتية من كومنز
صور وملفات صوتية من كومنز
- بوابة الفيزياء
- بوابة رياضيات
- بوابة طيران