سرعة الصوت

سرعة الصوت هي السرعة التي تنتقل بها الموجات الصوتيّة.[1][2][3]

طائرة F/A-18 أثناء اختراقها جدار الصوت الهالة أو الغيمة خلف الطائرة هي ماء متكثف بسبب فرق الضغط الّتي خلّفتة ورائها.

تختلف السرعة حسب الوسط الّذي تنتقل فيه الموجات. الخصائص التي تحدّد سرعة الصوت هي الكثافة ومعامل الحجم. ينتقل الصوت بسرعة أكبر خلال السوائل والأجسام الصلبة. كما أنّ سرعة الصوت تزداد مع الحرارة.

تقدّر سرعة الصوت في وسط هوائي عادي جاف في درجة حرارة (20 °C 68 °F) ب 343 متر في الثانية، أو (1,125 قدم/ثانية). أو ما يساوي 1235 كيلومتر في الساعة (768 ميل/الساعة)، أو ميل واحد في كل خمس ثوان.

العلاقة التي تربط بين سرعة الصوت والتردد $f$ وطول الموجة $\lambda \,$ هي :

v=\lambda \;f

.

وهي تنطبق في حالة الصوت كما تنطبق في حالة الضوء أو الموجات الكهرومغناطيسية، مع ملاحظة استبدال سرعة الصوت v بسرعة الضوء c في حالتي انتشار الضوء أو انتشار موجة كهرومغناطيسية.

التاريخ

تضمن كتاب مبادئ السير إسحاق نيوتن في سنة 1687 حسابًا لسرعة الصوت في الهواء بمقدار 979 قدم في الثانية (298 م/ث)، وهذه نسبة منخفضة بنحو 15٪.[4] وسبب التناقض يعود في المقام الأول إلى إهمال التأثير (غير المعروف آنذاك) لدرجات الحرارة المتقلبة بسرعة في الموجة الصوتية (بالمصطلحات الحديثة يعد ضغط الموجة الصوتية وتمدد الهواء عملية ثابتة الحرارة وليست عملية متساوية الحرارة). وقد صحح لابلاس ذلك الخطأ لاحقًا.[5]

وجرت عدة محاولات لقياس سرعة الصوت بدقة في القرن 17، ومنها محاولات مارين ميرسين سنة 1630 (1,380 قدمًا باريسيًا في الثانية)، وبيير جاسندي في سنة 1635 (1,473 قدمًا باريسيًا في الثانية)، ثم روبرت بويل (1125 قدمًا باريسيًا في الثانية).[6] وفي 1709 نشر القس ويليام ديرهام رئيس جامعة أبمينستر مقياسًا أكثر دقة لسرعة الصوت، عند 1،072 قدمًا باريسيًا في الثانية.[6] (كانت القدم الباريسية 325 مم. هذا أطول من "القدم الدولية" القياسية في الاستخدام الشائع اليوم، والتي تم تعريفها رسميًا في سنة 1959 على أنها 304.8 مم، مما يجعل سرعة الصوت تبلغ 20 °م (68 °ف) 1،055 قدم باريسي في الثانية).

استخدم ديرهام تلسكوبًا من برج كنيسة سانت لورانس في أبمينستر لمراقبة وميض بندقية بعيدة تم إطلاقها، ثم قاس الوقت حتى سمع طلقة نارية مع بندول نصف ثانية. وجرت قياس طلقات نارية أخرى من عدد من المعالم المحلية، ومنها كنيسة نورث أوكيندون. كانت المسافة معروفة بالتثليث، وبالتالي تم حساب السرعة التي قطعها الصوت.[7]

مفاهيم أساسية

يمكن توضيح نقل الصوت باستخدام نموذج يتكون من مجموعة من الأجسام الكروية المترابطة بواسطة الزنبرك.

من الناحية المادية الحقيقية، تمثل الكرات جزيئات المادة وتمثل الزنبركات الروابط بينها. يمر الصوت من خلال النظام عن طريق ضغط وتوسيع الزنبرك، مطلقا طاقة صوتية إلى الكرات المجاورة. ساعد هذا في نقل الطاقة بدوره إلى زنبرك الكرة المجاورة المرتبط به، ثم الذي يليه، وهكذا.

تعتمد سرعة الصوت خلال النموذج على جساءة/صلابة الزنبرك أو (النابض) وكتلة الكرات. وطالما أن التباعد بين الكرات يكون ثابتًا، فإن النوابض / الروابط الأكثر صلابة تنقل الطاقة بسرعة، بينما الكرات الأكبر تنقل طاقتها ببطئ.

في المادة الحقيقية تُعرف صلابة الزنبرك باسم معامل المرونة، وتتوافق الكتلة مع كثافة المادة. بالنظر إلى أن جميع الأشياء الأخرى متساوية مع ثبات باقي العوامل فإن الصوت سوف ينتقل بشكل أبطأ في المواد الإسفنجية، وأسرع في المواد الأكثر صلابة. يمكن أيضًا فهم التأثيرات مثل التشتت والانعكاس باستخدام هذا النموذج.

على سبيل المثال ينتقل الصوت في النيكل أسرع بـ 1.59 مرة منه في البرونز، بسبب زيادة صلابة النيكل عند نفس الكثافة تقريبًا. وبالمثل ينتقل الصوت في غاز الهيدروجين الخفيف (البروتيوم) أسرع بـ 1.41 مرة منه في غاز الهيدروجين الثقيل (الديوتيريوم)، لأن كثافة الديوتيريوم ضعف كثافة البروتيوم. وكذلك ينتقل الصوت "من النوع المضغوط" في المواد الصلبة أسرع منه في السوائل، وأسرع في السوائل عنه في الغازات، لأن المواد الصلبة أكثر صعوبة في الضغط من السوائل، وبدورها تكون السوائل أكثر صعوبة في الضغط من الغازات.

تذكر بعض الكتب التعليمية خطأً أن سرعة الصوت تزداد مع زيادة الكثافة. وتم توضيح هذه الفكرة من خلال تقديم بيانات لثلاث مواد، وهي الهواء والماء والصلب، ولكل منها انضغاط مختلف إلى حد كبير، وهو ما يعوض عن اختلافات الكثافة. مثال توضيحي للتأثيرين هو أن الصوت ينتقل في الماء أسرع بـ 4.3 مرات فقط من الهواء، على الرغم من الاختلافات الهائلة في انضغاط الوسيطتين. والسبب هو أن كثافة الماء الأكبر تعمل على إبطاء الصوت فيها مقارنة بالهواء، فتعوض تقريبًا عن اختلافات الانضغاط في الوسطين.

يمكن ملاحظة مثال عملي في إدنبرة عندما تم إطلاق "مدفع الساعة الواحدة" في الطرف الشرقي لقلعة إدنبرة. عند الوقوف عند قاعدة الطرف الغربي من Castle Rock، يمكن سماع صوت البندقية من خلال الصخرة قبل وصوله عن طريق الهواء، متأخراً جزئياً بسبب الطريق الأطول قليلاً.

موجات انضغاط وعرضية

موجة طولية خاصة بطائرة. هذه هي الموجة الوحيدة التي من موجات الصوت التي تنتشر في الموائع (غاز وسائل). الموجة العرضية أيضا يمكنها الانتشار في المواد الصلبة.

في الغاز أو السائل، يتكون الصوت من موجات انضغاطية. في المواد الصلبة، تنتشر الموجات ويكون لها نوعين مختلفين. الموجة الطولية وهي متعلقة بالانضغاط وإزالة الانضغاط في اتجاه السريان. تنتشر الموجات الانضغاطية في السوائل والغازات. هناك نوع إضافي للموجات وهي الموجات العرضية والتي تنتشر في فقط في المواد الصلبة. وهذا بسبب التشوه المرن الذي يحدث بشكل عمودي على اتجاه انتشار الموجة. اتجاه التشوه لهذا النوع من الموجات يسمى الاستقطاب. في العموم فإن الموجات العرضية تحدث كزوج من الاستقطاب العمودي.

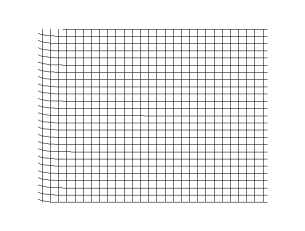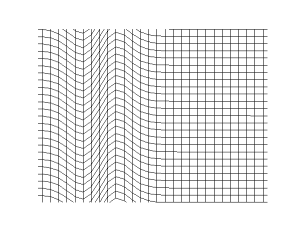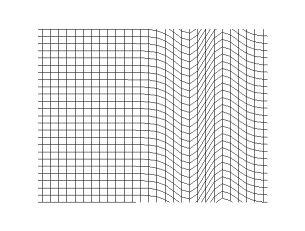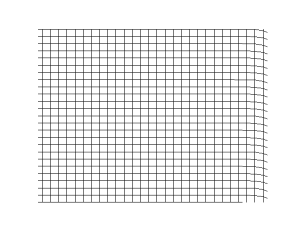
موجة عرضية تنتشر فقط في المواد الصلبة

هذه الموجات المختلفة ربما يكون لها سرعات مختلفة حتى وإن كان لها تردد واحد. لذلك فهي تصل إلى الملاحظ في أزمنة مختلفة، على سبيل المثال الزلازل حيث تصل الموجة الانضغاطية أولا ومن ثم الموجة العرضية.

تحدد سرعة الموجة الانضغاطية في المائع حسب انضاغطية الوسط وكثافته. في المواد الصلبة فإن الموجات الانضغاطية مشابهه لتلك الموجات في الموائع اعتمادا على الانضغاطية، الكثافة ومعامل القص. سرعة موجات القص والتي تنتشر في المواد الصلبة يتم تحديدها بمعامل القص للمواد الصلبة والكثافة.

سرعة الصوت في الغازات والسوائل

ينتقل الصوت في الغازات والسوائل عن طريق انتشار موجات الضغط والكثافة حيث تتذبذب الجزيئات فيها في اتجاه انتشار الصوت (أي تتأرجح جزيئات الوسط إلى الأمام وإلى الخلف وهكذا من دون أن تنتقل من مكانها. تلك الحركة تسمى موجة طولية. وتكون سرعة الصوت هي دالة لكثافة $\rho \,$ الوسط ومعامل الحجم $K$ (أي قابلية المادة على الانضغاط)؛ وهذه المعادلة تنطبق على الغازات والسوائل.

c_{\mathrm {Fl{\ddot {u}}ssigkeit,Gas} }={\sqrt {\frac {K}{\rho }}}

.

أي ان سرعة الصوت في وسط غازي أو سائل تزداد بزيادة قابلية الوسط على الانضغاط وتقل مع زيادة كثافة الوسط. يمكن تعميم المعادلة العامّة لسرعة الصوت باستخدام الميكانيكا الكلاسيكيّة:

c^{2}={\frac {\partial p}{\partial \rho }}

أي باشتقاق نسبة التغيّر الأديباتي.

في حالة أخذ النسبيّة الخاصّة بعين الاعتبار، يمكن اشتقاق سرعة الصوت من معادلات ايولر النسبيّة.

تكون السرعة مستقلّة عن التردّد إذا كان الوسط غير متبدّد أمّا إذا كان متبدّدا فتكون السرعة دالة في التردّد. مثلا يعتبر الهواء وسط غير متبدّد عند التردّدات السمعيّة ثمّ يصبح متبدّدا عند التردّدات فوق السمعية بسبب وجود ثاني أكسيد الكربون في الهواء الجوّي وهو وسط متبدّد.

اختلاف الارتفاع وآثاره على الصوتيات الجوية

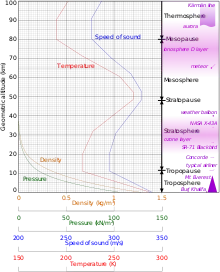
تنخفض الكثافة والضغط بسلاسة مع الارتفاع، لكن درجة الحرارة (الأحمر) لا تقل. تعتمد سرعة الصوت (الأزرق) فقط على التباين المعقد في درجة الحرارة عند الارتفاع ويمكن حسابها منه نظرًا لأن تأثيرات الكثافة والضغط المعزولة على سرعة الصوت تلغي بعضها البعض. تزداد سرعة الصوت مع الارتفاع في منطقتين من الستراتوسفير والغلاف الحراري، بسبب تأثيرات التسخين في هذه المناطق.

في الغلاف الجوي للأرض فإن العامل الرئيسي الذي يؤثر على سرعة الصوت هو درجة الحرارة. لذلك ففي حالة غاز مثالي معين بسعة حرارية ثابتة وتركيب ثابت، فإن سرعة الصوت تعتمد فقط على درجة الحرارة؛ انظر التفاصيل بالأسفل. في مثل هذه الحالة المثالية، فإن تأثيرات الكثافة المنخفضة وضغط الارتفاع المنخفض تلغي بعضها البعض حافظًا التأثير المتبقي لدرجة الحرارة.

نظرًا لأن درجة الحرارة (وبالتالي سرعة الصوت) تنخفض مع زيادة الارتفاع حتى 11 كم، فإن الصوت ينكسر إلى الأعلى، بعيدًا عن المستمعين على الأرض، مما يخلق ظلًا صوتيًا على مسافة ما من المصدر.[8] ويشار إلى انخفاض سرعة الصوت مع الارتفاع على أنه تدرج سرعة الصوت السلبي ^{[الإنجليزية]}.

ومع ذلك، هناك اختلافات في هذا الاتجاه فوق 11 كم. على وجه الخصوص في طبقة الستراتوسفير التي تزيد عن 20 كم، تزداد سرعة الصوت مع الارتفاع، بسبب زيادة درجة الحرارة من التسخين داخل طبقة الأوزون. ينتج عن هذا سرعة موجبة لتدرج الصوت في هذه المنطقة. لا تزال توجد منطقة أخرى من التدرج الإيجابي على ارتفاعات عالية جدًا، في الغلاف الحراري المسمى بشكل مناسب فوق 90 كم.

صيغة تطبيقيّة للهواء الجاف

تعطى سرعة الصوت في الهواء الجاف (0% رطوبة) بالعلاقة:

c_{\mathrm {air} }=331.3\mathrm {m\cdot s^{-1}} {\sqrt {1+{\frac {T}{273.15^{\circ }\mathrm {C} }}}}\

حيث $T$ هي درجة الحرارة المئوية (°C).

يمكن استخدام العلاقة التقريبية أيضا عند درجات حرارة قريبية من الصفر المئوي باستخدام مفكوك تايلور للعلاقة السابقة والتوقف عند الحدّ الثاني:

c_{\mathrm {air} }=(331{.}3+(0{.}606^{\circ }\mathrm {C} ^{-1}\cdot T))\ \mathrm {m\cdot s^{-1}} \,

لاحظ ان سرعة الصوت تصبح 331.3 م\ث عند الصفر المئوي وقد تمّ الحصول عليها من افتراض قانون الغاز المثالي (انظر التفاصيل بالأسفل).

التفاصيل

السرعة في الغاز المثالي والهواء

c={\sqrt {\gamma \cdot {p \over \rho }}}

حيث:

\gamma

معامل ثبات الاعتلاج وهو يمثل النسبة بين السّعة الحراريّة للغاز عند ثبات الضغط إلى السعة الحرارية عند ثبات الحجم. (للهواء :

C_{p}/C_{v}=1.4

),.

p الضغط.

$\rho$ الكثافة

ولكن في الغاز المثالي,

p={\frac {nRT}{V}}\,

وبالتعويض عن ρ بـnM/V، تصبح العلاقة كالتّالي:

c_{\mathrm {ideal} }={\sqrt {\gamma \cdot {p \over \rho }}}={\sqrt {\gamma \cdot R\cdot T \over M}}={\sqrt {\gamma \cdot k\cdot T \over m}}

حيث

$c_{\mathrm {ideal} }$ سرعة الصوت في الغاز المثالي.
$R$ (تقريبا 8.3145 J·mol⁻¹·K⁻¹) الثابت الجزيئي للغاز.
$k$ ثابت بولتزمان
$\gamma$ (جاما) العامل الأديباتي.
$T$ الحرارة المطلقة مقدرة بال كلفن.
$M$ الكتلة الجزيئية بالكيلوجرام لكل مول,
$m$ كتلة الجزيء الواحد بالكيلوجرام.

التأثيرات الناتجة عن ريح القص

تختلف سرعة الصوت باختلاف درجة الحرارة. ولأن درجة الحرارة وسرعة الصوت تتناقصان عادةً مع زيادة الارتفاع، فينكسر الصوت لأعلى مبتعدا عن المستمعين على الأرض، مما يخلق ظلًا صوتيًا على مسافة ما من المصدر.[8] فيمكن لريح القص بسرعة 4 م/ث أن تنتج انكسار يساوي معدل سقوط درجة حرارة نموذجية من 7.5 س°/ كم.[9] فازدياد القيم في تدرج الرياح يجعل الصوت ينكسر نحو الأسفل إلى السطح بوجهة الريح،[10] فيقضي على الظل الصوتي مع اتجاه الريح. مما يؤدي إلى زيادة سماع الأصوات مع اتجاه الريح. فتأثير الانكسار مع اتجاه الريح يكون بسبب تدرج للرياح؛ لأن الصوت لا تحمله الريح.[11]

لانتشار الصوت يمكن تعريف التباين الأسي لسرعة الرياح مع الارتفاع على النحو التالي:[12]

U(h)=U(0)h^{\zeta },

{\frac {\mathrm {d} U}{\mathrm {d} H}}(h)=\zeta {\frac {U(h)}{h}},

حيث

U ( h ) هي سرعة الرياح على ارتفاع h ؛
ζ هو المعامل الأسي على أساس خشونة سطح الأرض، عادة بين 0.08 و 0.52 ؛
d U / d H ( h ) هو تدرج الرياح المتوقع عند الارتفاع h.

ففي سنة 1862 خلال معركة إيوكا في الحرب الأهلية الأمريكية تمكن الظل الصوتي الذي يُعتقد أنه تم تعزيزه بفعل الرياح الشمالية الشرقية في إبقاء فرقتين من جنود الاتحاد خارج المعركة،[13] لأنهم لم يتمكنوا من سماع أصوات المعركة سوى 10 كم (ستة أميال) مع اتجاه الريح.

الجداول

في الجو القياسي:

T ₀ يكون ‏K‏ 273.15 حيث (= °C ‏0 و °F‏ 32)، يعطي القيمة النظرية لل 331.3 م/ث (=1086.9 قدم/ث = 1193 كم/ساعة = 741.1 م/س = 644.0 عقدة). ويمكن العثور على قيم تتراوح من 331.3 إلى 331.6 م/ث في الأدبيات المرجعية، مثال؛
T ₂₀ يكون ‏K‏ 293.15، حيث (= °C ‏20 و °F‏ 68)، يعطي قيمة 343.2 م/ث (= 1126.0 قدم/ثانية =1236 كم/س = 767.8 م/س =667.2 عقدة)؛
T ₂₅ هو 298.15 K (= °C ‏25 و °F‏ 77)، يعطي قيمة 346.1 م/ث (= 1135.6 قدم/ث =1246 كم/ساعة = 774.3 م/س =672.8 عقدة).

واقعيا وبافتراض وجود غاز مثالي، فإن سرعة الصوت c تعتمد على درجة الحرارة فقط، وليس على الضغط أو الكثافة. فالهواء الجوي هو تقريبا غاز مثالي. وتختلف درجة حرارة الهواء باختلاف الارتفاع، مما يعطي الاختلافات التالية في سرعة الصوت باستخدام الغلاف الجوي القياسي - قد تختلف الظروف الفعلية.

تأثير درجة الحرارة على خصائص الهواء
درجة الحرارة T ( درجة مئوية )	سرعة الصوت ج ( م/ث )	كثافة الهواء ρ ( كجم/ م ³ )	المقاومة الصوتية المحددة المميزة z ₀ ( Pa · م / ث )
35	351.88	1.1455	403.2
30	349.02	1.1644	406.5
25	346.13	1.1839	409.4
20	343.21	1.2041	413.3
15	340.27	1.2250	416.9
10	337.31	1.2466	420.5
5	334.32	1.2690	424.3
0	331.30	1.2922	428.0
−5	328.25	1.3163	432.1
−10	325.18	1.3413	436.1
−15	322.07	1.3673	440.3
−20	318.94	1.3943	444.6
−25	315.77	1.4224	449.1

في ظل الظروف الجوية العادية، تختلف درجة الحرارة، وبالتالي سرعة الصوت، باختلاف الارتفاع:

ارتفاع	درجة الحرارة	الآنسة	كم / ساعة	ميلا في الساعة	كن
مستوى سطح البحر	15 درجة مئوية (59 درجة فهرنهايت)	340	1،225	761	661
11000 م-20000 م ( الابحار على ارتفاع الطائرات التجارية، وأول رحلة أسرع من الصوت )	−57 درجة مئوية (−70 درجة فهرنهايت)	295	1،062	660	573
29000 م (رحلة X-43A )	−48 درجة مئوية (−53 درجة فهرنهايت)	301	1.083	673

تأثير التردد وتكوين الغاز

اعتبارات فيزيائية عامة

لاتكون استجابة الوسط الذي انتقلت فيه الموجة الصوتية منتظمة، ونتيجة لذلك يمكن أن تختلف سرعة الصوت باختلاف التردد.[14]

وهناك اهتمام حول التوهين الشديد الذي قيّد مفهوم سرعة الصوت. فالتوهين الموجود عند مستوى سطح البحر للترددات العالية ينطبق على الترددات المنخفضة عند انخفاض الضغط الجوي، أو عند زيادة متوسط المسار الحر. لهذا السبب فإن مفهوم سرعة الصوت (باستثناء الترددات التي تقترب من الصفر) يفقد تدريجياً نطاق قوته في الارتفاعات العالية.[15] وتنطبق المعادلات القياسية لسرعة الصوت بدقة معقولة فقط على المواقف التي يكون فيها طول الموجة الصوتية أعلى بكثير من متوسط المسار الحر للجزيئات في الغاز.

ساهم التركيب الجزيئي للغاز بالتأثير على سرعة الصوت من حيث كتلة الجزيئات (M) والقدرة الحرارية. بشكل عام تمتلك الغازات أحادية الذرة عند نفس الكتلة الجزيئية سرعة صوت أعلى قليلاً (فوق 9٪) لأن لديها γ أعلى ( 5/3 = 1.66 ...) من ثنائي الذرة ( 7/5 = 1.4 ). وبذا عند نفس الكتلة الجزيئية يرتفع سرعة صوت غاز أحادي الذرة بمعامل قدره

{c_{\mathrm {gas,monatomic} } \over c_{\mathrm {gas,diatomic} }}={\sqrt {{5/3} \over {7/5}}}={\sqrt {25 \over 21}}=1.091\ldots

هذا يعطي فرق الـ 9٪، وهي نسبة نموذجية لسرعة الصوت في درجة حرارة الغرفة بالهيليوم مقابل الديوتيريوم ولكل منهما وزن جزيئي 4. ويكون الصوت أسرع في الهيليوم من الديوتيريوم لأن ضغط ثابت الحرارة للهيليوم يسخن أكثر، بحيث يمكن لجزيئات الهيليوم تخزين طاقة حرارة ناتجة عن الانضغاط فقط عند الانتقال وليس الدوران. وهكذا تنتقل جزيئات الهليوم (جزيئات أحادية الذرة) أسرع في موجة صوتية وتنقل الصوت بشكل أسرع. (ينتقل الصوت بحوالي 70٪ من متوسط السرعة الجزيئية في الغازات: 75٪ في الغازات أحادية الذرة و 68٪ في الغازات ثنائية الذرة).

لاحظ أنه في هذا المثال افترضنا أن درجة الحرارة منخفضة بدرجة كافية بحيث لا تتأثر السعات الحرارية بالاهتزاز الجزيئي. ومع ذلك فإن أنماط الاهتزاز تسبب جاما بالانخفاض إلى النمط 1، لأن أوضاع الاهتزاز في غاز متعدد الذرات تعطي الغاز طرقًا إضافية لتخزين الحرارة دون التأثير على درجة حرارتها، وبالتالي لا تؤثر على السرعة الجزيئية وسرعة الصوت. ومن ثم فإن تأثير درجات الحرارة المرتفعة والسعة الحرارية الاهتزازية يعمل على زيادة الفرق في سرعة الصوت بين الجزيئات أحادية الذرة والجزيئات متعددة الذرات، مع بقاء السرعة أعلى في أحادية الذرة.

تطبيق عملي على الهواء

تعتبر الحرارة هي العامل الأكثر أهمية الذي يؤثر على سرعة الصوت في الهواء. فالسرعة تتناسب طرديًا مع الجذر التربيعي لدرجة الحرارة المطلقة، مما يزيد بمقدار 0.6 م/ث لكل درجة مئوية. لهذا السبب تزداد نغمة آلة النفخ الموسيقية مع زيادة درجة حرارتها.

وكذلك تتناسب طرديا مع الرطوبة ولكن عكسيا مع ثاني أكسيد الكربون. الفرق بين 0٪ و 100٪ رطوبة حوالي 1.5 م/ث عند الضغط والحرارة القياسيين، لكن مدى تأثير الرطوبة يزداد بشكل كبير مع الحرارة.

عادة ما يكون الاعتماد على التردد والضغط غير مهم في التطبيقات العملية. وفي الهواء الجاف تزداد سرعة الصوت بنحو 0.1 م/ث حيث يرتفع التردد من 10 هرتز إلى 100 هرتز. أما الترددات الصوتية التي تزيد عن 100 هرتز فهي ثابتة نسبيًا. يتم تحديد القيم القياسية لسرعة الصوت في حدود الترددات المنخفضة، حيث يكون الطول الموجي كبيرًا مقارنة بمتوسط المسار الحر. [16]

كما هو موضح أعلاه القيمة التقريبية 1000/3 = 333.33 ... م/ث هي أقل بقليل من 5 درجات مئوية وهو تقدير تقريبي لجميع الحرارة الخارجية "المعتادة" (في المناخات المعتدلة على الأقل)، ومن هنا جاءت القاعدة العامة المعتادة لتحديد مسافة ضرب البرق: عد الثواني من بداية الوميض إلى بداية صوت الرعد المرتبط وتقسيمها على 3: النتيجة هي المسافة بالكيلومترات لأقرب نقطة للصاعقة.

رقم ماخ

يعتبر معامل أو رقم ماخ مفيدا في حساب سرعة جسم ما نسبة إلى سرعة الصوت وهو دالة في الحرارة. إلا أن أدوات طيران الطائرات تستخدم فرق الضغط لحساب رقم ماخ وليس درجة الحرارة. بافتراض هو أن ضغطًا معينًا يمثل ارتفاعًا معينًا ومن ثم درجة حرارة قياسية. وتحتاج أدوات طيران الطائرات إلى العمل بهذه الطريقة لأن ضغط الركود الذي يتم استشعاره بواسطة أنبوب بيتوت يعتمد على الارتفاع بالإضافة إلى السرعة.

قياسات تجريبيّة

توجد مجموعة من الطرق المختلفة لقياس الصوت في الهواء.

أول تقدير دقيق نوعا ما لسرعة الصوت في الهواء أجراها ويليام ديرهام واعترف بها إسحاق نيوتن. كان لدى ديرهام تلسكوب أعلى برج كنيسة سانت لورانس في أبمينستر بإنجلترا. وفي يوم هادئ كانت ساعة متزامنة لمساعد قام بإطلاق بندقية في وقت محدد مسبقًا من نقطة بارزة على بعد بضعة أميال عبر الريف، ومراقبة عن طريق التلسكوب. ثم قيس الفاصل الزمني بين رؤية دخان السلاح ووصول الصوت باستخدام بندول مدته نصف ثانية. وتقاس المسافة إطلاق البندقية عن طريق التثليث، وقدم التقسيم البسيط (المسافة / الوقت) لإعطاء السرعة. أخيرًا من خلال إجراء العديد من الملاحظات، وباستخدام مجموعة من المسافات المختلفة أمكن حساب متوسط عدم دقة البندول الذي يبلغ نصف ثانية، مما أعطي تقديره النهائي لسرعة الصوت. تتيح ساعات التوقف الحديثة استخدام هذه الطريقة اليوم على مسافات قصيرة تصل إلى 200-400 متر، ولا تحتاج إلى شيء بصوت عالٍ مثل بندقية.

هناك عدّة طرق لحساب سرعة الصوت تجريبيّا إحداها طريقة الصدمة حيث يتمّ ملاحظة تصادم بين جسمين من مسافة معيّنة وتسجيل فرق الزّمن بين مشاهدة حدث التصادم وسماع الصوت. نظرا لأنّ مشاهدة الحدث تـمّت بفضل الضوء وسرعته لاتقارن بسرعة الصوت فيمكن مباشرة قسمة المسافة على الفارق الزّمني والحصول على سرعة الصوت. الطريقة الأخرى تتمثّل في إلغاء عامل الزّمن واستعاضته بالقيّاس التردّدي. تعتبر انبوبة كندت خير مثال على ذلك حيث يمكن بها قياس سرعة الصّوت في أيّ غاز.

بافتراض غاز مثالي يمكن اشتقاق رقم ماخ لتدفق تحت صوتي انضغاطي من معادلة بيرنولي.

{M}={\sqrt {5\left[\left({\frac {q_{c}}{P}}+1\right)^{\frac {2}{7}}-1\right]}}

حيث

M

رقم ماخ

q_{c}

الضغط المؤثر

P

الضغط الساكن.

وتشتق معادلة حساب رقم ماخ في جريان انضغاطي فوق صوتي من رقم رايلاي:

{M}=0.88128485{\sqrt {\left[\left({\frac {q_{c}}{P}}+1\right)\left(1-{\frac {1}{[7M^{2}]}}\right)^{2.5}\right]}}

يلاحظ وجود رقم ماخ في طرفي المعادلة وبالتّالي يتمّ حلّ المعادلة بالتحليل العددي والاستعانة بالحاسوب.

سرعة الصوت في الأجسام الصلبة

ينتقل الصوت في الأجسام الصلبة في هيئة موجة طولية (حيث تكون اتجاه أرجحة الجزيئات موازيا لاتجاه تقدم الموجة) وكذلك في هيئة موجة عرضية (حيث يكون اتجاه تأرجح الجزيئات عموديا على اتجاه تقدم الموجة).

وبالنسبة للموجة الطولية في مادة صلبة تعتمد سرعة الصوت على كثافة $\rho \,$ المادة، ونسبة بواسون $\mu \,$ ومعامل يونغ $E$ للمادة. وتنطبق المعادلتان :

انتشار موجة طولية في مادة صلبة:

c_{\mathrm {Festk{\ddot {o}}rper,\,longitudinal} }={\sqrt {\frac {E\,(1-\mu )}{\rho \,(1-\mu -2\mu ^{2})}}}

و

انتشار موجة عرضية في مادة صلبة:

c_{\mathrm {Festk{\ddot {o}}rper,\,transversal} }={\sqrt {\frac {E}{2\,\rho \,(1+\mu )}}}

سرعة الصوت في السوائل

تعطى بالعلاقة:

c_{\mathrm {fluid} }={\sqrt {\frac {K}{\rho }}}

حيث

K معامل الحجم للسائل.

انظر أيضًا

مراجع

"معلومات عن سرعة الصوت على موقع britannica.com". britannica.com. مؤرشف من الأصل في 12 يونيو 2019. الوسيط |CitationClass= تم تجاهله (مساعدة)
"معلومات عن سرعة الصوت على موقع d-nb.info". d-nb.info. مؤرشف من الأصل في 26 يناير 2020. الوسيط |CitationClass= تم تجاهله (مساعدة)
"معلومات عن سرعة الصوت على موقع jstor.org". jstor.org. مؤرشف من الأصل في 10 يناير 2020. الوسيط |CitationClass= تم تجاهله (مساعدة)
"The Speed of Sound". mathpages.com. مؤرشف من الأصل في 25 يوليو 2020. اطلع عليه بتاريخ 03 مايو 2015. الوسيط |CitationClass= تم تجاهله (مساعدة)
Bannon, Mike; Kaputa, Frank. "The Newton–Laplace Equation and Speed of Sound". Thermal Jackets. مؤرشف من الأصل في 15 أغسطس 2020. اطلع عليه بتاريخ 03 مايو 2015. الوسيط |CitationClass= تم تجاهله (مساعدة)
Murdin, Paul (25 December 2008). Full Meridian of Glory: Perilous Adventures in the Competition to Measure the Earth. Springer Science & Business Media. صفحات 35–36. ISBN 9780387755342. الوسيط |CitationClass= تم تجاهله (مساعدة)
Fox, Tony (2003). Essex Journal. Essex Arch & Hist Soc. صفحات 12–16. الوسيط |CitationClass= تم تجاهله (مساعدة)
Everest, F. (2001). The Master Handbook of Acoustics. New York: McGraw-Hill. صفحات 262–263. ISBN 978-0-07-136097-5. الوسيط |CitationClass= تم تجاهله (مساعدة)
Uman, Martin (1984). Lightning. New York: Dover Publications. ISBN 978-0-486-64575-9. الوسيط |CitationClass= تم تجاهله (مساعدة)
Volland, Hans (1995). Handbook of Atmospheric Electrodynamics. Boca Raton: CRC Press. صفحة 22. ISBN 978-0-8493-8647-3. الوسيط |CitationClass= تم تجاهله (مساعدة)
Singal, S. (2005). Noise Pollution and Control Strategy. Oxford: Alpha Science International. صفحة 7. ISBN 978-1-84265-237-4. It may be seen that refraction effects occur only because there is a wind gradient and it is not due to the result of sound being convected along by the wind. الوسيط |CitationClass= تم تجاهله (مساعدة)
Bies, David (2009). Engineering Noise Control, Theory and Practice. London: CRC Press. صفحة 249. ISBN 978-0-415-26713-7. As wind speed generally increases with altitude, wind blowing towards the listener from the source will refract sound waves downwards, resulting in increased noise levels. الوسيط |CitationClass= تم تجاهله (مساعدة)
Cozens, Peter (2006). The Darkest Days of the War: the Battles of Iuka and Corinth. Chapel Hill: The University of North Carolina Press. ISBN 978-0-8078-5783-0. الوسيط |CitationClass= تم تجاهله (مساعدة)
A B Wood, A Textbook of Sound (Bell, London, 1946)
U.S. Standard Atmosphere, 1976, U.S. Government Printing Office, Washington, D.C., 1976.
"Speed of Sound in Air". Phy.mtu.edu. مؤرشف من الأصل في 23 يونيو 2017. اطلع عليه بتاريخ 13 يونيو 2014. الوسيط |CitationClass= تم تجاهله (مساعدة)

في كومنز صور وملفات عن: سرعة الصوت

بوابة الفيزياء

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.

[1] "معلومات عن سرعة الصوت على موقع britannica.com". britannica.com. مؤرشف من الأصل في 12 يونيو 2019. الوسيط |CitationClass= تم تجاهله (مساعدة)

[2] "معلومات عن سرعة الصوت على موقع d-nb.info". d-nb.info. مؤرشف من الأصل في 26 يناير 2020. الوسيط |CitationClass= تم تجاهله (مساعدة)

[3] "معلومات عن سرعة الصوت على موقع jstor.org". jstor.org. مؤرشف من الأصل في 10 يناير 2020. الوسيط |CitationClass= تم تجاهله (مساعدة)

[4] "The Speed of Sound". mathpages.com. مؤرشف من الأصل في 25 يوليو 2020. اطلع عليه بتاريخ 03 مايو 2015. الوسيط |CitationClass= تم تجاهله (مساعدة)

[5] Bannon, Mike; Kaputa, Frank. "The Newton–Laplace Equation and Speed of Sound". Thermal Jackets. مؤرشف من الأصل في 15 أغسطس 2020. اطلع عليه بتاريخ 03 مايو 2015. الوسيط |CitationClass= تم تجاهله (مساعدة)

[meridian-6] Murdin, Paul (25 December 2008). Full Meridian of Glory: Perilous Adventures in the Competition to Measure the Earth. Springer Science & Business Media. صفحات 35–36. ISBN 9780387755342. الوسيط |CitationClass= تم تجاهله (مساعدة)

[Tony_Fox-7] Fox, Tony (2003). Essex Journal. Essex Arch & Hist Soc. صفحات 12–16. الوسيط |CitationClass= تم تجاهله (مساعدة)

[Everest2001-8] Everest, F. (2001). The Master Handbook of Acoustics. New York: McGraw-Hill. صفحات 262–263. ISBN 978-0-07-136097-5. الوسيط |CitationClass= تم تجاهله (مساعدة)

[9] Uman, Martin (1984). Lightning. New York: Dover Publications. ISBN 978-0-486-64575-9. الوسيط |CitationClass= تم تجاهله (مساعدة)

[10] Volland, Hans (1995). Handbook of Atmospheric Electrodynamics. Boca Raton: CRC Press. صفحة 22. ISBN 978-0-8493-8647-3. الوسيط |CitationClass= تم تجاهله (مساعدة)

[11] Singal, S. (2005). Noise Pollution and Control Strategy. Oxford: Alpha Science International. صفحة 7. ISBN 978-1-84265-237-4. It may be seen that refraction effects occur only because there is a wind gradient and it is not due to the result of sound being convected along by the wind. الوسيط |CitationClass= تم تجاهله (مساعدة)

[12] Bies, David (2009). Engineering Noise Control, Theory and Practice. London: CRC Press. صفحة 249. ISBN 978-0-415-26713-7. As wind speed generally increases with altitude, wind blowing towards the listener from the source will refract sound waves downwards, resulting in increased noise levels. الوسيط |CitationClass= تم تجاهله (مساعدة)

[13] Cozens, Peter (2006). The Darkest Days of the War: the Battles of Iuka and Corinth. Chapel Hill: The University of North Carolina Press. ISBN 978-0-8078-5783-0. الوسيط |CitationClass= تم تجاهله (مساعدة)

[14] A B Wood, A Textbook of Sound (Bell, London, 1946)

[USSA1976-15] U.S. Standard Atmosphere, 1976, U.S. Government Printing Office, Washington, D.C., 1976.

[16] "Speed of Sound in Air". Phy.mtu.edu. مؤرشف من الأصل في 23 يونيو 2017. اطلع عليه بتاريخ 13 يونيو 2014. الوسيط |CitationClass= تم تجاهله (مساعدة)