خوارزمية ديكسترا
خوارزمية ديكسترا (بالإنجليزية: Dijkstra's algorithm) هي خوارزمية تعنى بحل مسألة إيجاد المسار الأقصر بين عقدتين في بيان لا يحتوي على وصلات ذات أوزان سلبية.[1][2][3] الخوارزمية مفيدة في عدة تطبيقات، مثل إيجاد الطريق الأقصر بين مدينتين ضمن خريطة، حيث قد تمثل أوزان الوصلات طول الشارع أو مستوى الازدحام في ذلك الشارع أو مجموعهما أو أي معيار مناسب آخر. واضع هذه الخوارزمية هو الهولندي ادسخر دكسترا سنة 1959.
| خوارزمية ديكسترا | |
|---|---|
 | |
| بيانات عامّة | |
| الصنف | خوارزمية بحث |
| بنية البيانات | بيان |
| الأداء في أسوء حالة | |
تعريف المسألة
لدينا بيان حيث انه بيان موزون ومترابط، أوزان وصلاته غير سالبة: ، ولتكن عقدتين ضمن هذا البيان.
نريد أن نجد مساراً بسيطاً يربط بين s و-t على أن يكون وزن هذا المسار (المُعرّف على أساس مجموع أوزان الوصلات التي يتألف منها) أصغر ما يمكن.
هذه هي المسألة بشكل عام ولكن الخوارزمية تحل مسألة أكثر عموميةً من هذه تتمثل في إيجاد أقصر مسار بين العقدة v وجميع العقد الأخرى.
الخوارزمية

شرح الخوارزمية
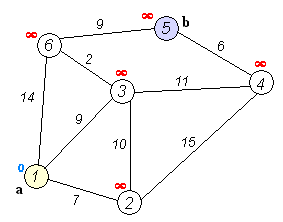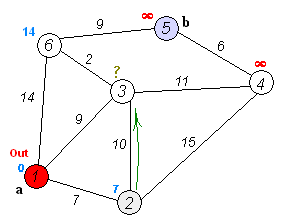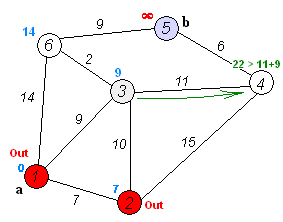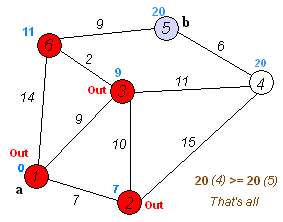
سنطلق على العقدة التي نبدأ منها اسم العقدة الأولية. لتكن المسافة حتى العقدة Y هي المسافة من العقدة الأولية حتى العقدة Y. ستقوم خوارزمية دايكسترا بإسناد قيم معينة للمسافات وتحاول بعد ذلك القيام بتحسين هذه المسافات خطوة بعد خطوة.
- أسند لكل عقدة قيمة ما تمثل المسافة: دع هذه القيمة صفراً بالنسبة للعقدة الأولية، ولانهاية بالنسبة لباقي العقد.
- علّم كافة العقد بأنها غير مزارة، علّم العقدة الأولية بأنها العقدة الحالية. اصنع مجموعة من العقد التي لم تتم زيارتها بعد وادعُ هذه المجموعة مجموعة العقد غير المزارة، تتضمن هذه المجموعة بدايةً كافة العقد.
- قم بتحديد كافة جيران العقدة الحالية واحسب المسافات من هذه العقد إلى العقدة الحالية. قارن المسافات الجديدة مع المسافات القديمة واختر الأصغر. على سبيل المثال، لتكن العقدة الحالية A معلّمة بالمسافة 6، وليكن الضلع (الحافة) التي تصل A بالعقدة B بطول مقداره 2، وبالتالي فإن المسافة حتى العقدة B (من خلال العقدة A) ستكون 6+2=8. إذا كانت B معلمة سابقاً بمسافة أقل من 8 عندئذ لا نغير قيمة B، وإذا لم تكن كذلك فإننا نقوم بتغييرها.
- عند الانتهاء من تعيين قيم كافة جيران العقدة الحالية، فإننا نعلم العقدة الحالية بأنها عقدة مزارة ونحذفها من مجموعة العقدة غير المزارة بحيث لا نقوم لاحقاً بإعادة زيارتها.
- إذا تم تعليم العقدة الهدف بأنها عقدة مزارة (في حال البحث عن مسار بين عقدتين معطيتين) أو إذا كانت المسافة الأصغر من بين كافة العقد الموجودة في مجموعة العقد غير المزارة (في حال البحث عن جولة كاملة؛ يحدث ذلك في حال عدم وجود اتصال بين العقدة الأولية وباقي العقد غير المزارة) عندئذ يجب أن نتوقف وينتهي عمل الخوارزمية.
- اختر العقدة غير المزارة التي لديها المسافة الأصغر وعلّم هذه العقدة بأنها العقدة الحالية وعُد إلى الخطوة 3.
الخوارزمية تعتمد بشكل كبير على انه إذا وجدنا المسار الأقصر بين v و-u لنُسمه بحيث أن k هو طول المسار ووزنه هو و- , حينئذ إذا نظرنا للمسارات الجزئية من v حتى نجد حينها أنها هي الأقصر. وهذه المُعاينة تعتمد على أنَّ الأوزان موجبة .
كود الخوارزمية
ما يلي هو تطبيق الخوارزمية بلغة java,[4] وهذا التطبيق هو ليس الأفضل بالضرورة ولكنه نموذج لطريقة التطبيق :
class Dijkstra
{
double[] dist = new double[G.V()];
Edge[] pred = new Edge[G.V()];
public Dijkstra(WeightedDigraph G, int s)
{
boolean[] marked = new boolean[G.V()];
for (int v = 0; v <G.V(); v++)
dist[v] = Double.POSITIVE_INFINITY;
MinPQplus<Double, Integer> pq;
pq = new MinPQplus<Double, Integer>(); \\Priority Queue
dist[s] = 0.0;
pq.put(dist[s], s);
while (!pq.isEmpty())
{
int v = pq.delMin();
if (marked[v]) continue;
marked(v) = true;
for (Edge e : G.adj(v))
{
int w = e.to();
if (dist[w]> dist[v] + e.weight())
{
dist[w] = dist[v] + e.weight();
pred[w] = e;
pq.insert(dist[w], w);
}
}
}
}
}
الإستخدامات
تستخدم هذه الخوارزمية بشكل رئيسي في تطبيقات حساب الطرق مثل خرائط جوجل. فبفضل هذه الخوارزمية يتم إيجاد أقصر طريق بين موقعين. حيث يتم تمثيل شبكة الطرق على شكل رسم بياني والمواقع على شكل عُقد أو نقاط في هذه الشبكة، ومن ثم يتم حساب أقرب مسافة في هذه الشبكة بين أي نقطتين فيها.
كذلك تستخدم هذه الخوارزمية في مجال شبكات الإنترنت كخوارزمية توجيه في بعض البروتوكولات مثل: بروتوكول الربط بين الأنظمة الوسيطية.
روابط خارجية
مراجع
- Bauer, Reinhard; Delling, Daniel; Sanders, Peter; Schieferdecker, Dennis; Schultes, Dominik; Wagner, Dorothea (2010). "Combining hierarchical and goal-directed speed-up techniques for Dijkstra's algorithm". J. Experimental Algorithmics. 15. الوسيط
|CitationClass=تم تجاهله (مساعدة) - Sniedovich, M. (2006). "Dijkstra's algorithm revisited: the dynamic programming connexion" (PDF). Journal of Control and Cybernetics. 35 (3): 599–620. مؤرشف من الأصل (نسق المستندات المنقولة) في 15 فبراير 2020. الوسيط
|CitationClass=تم تجاهله (مساعدة) نسخة محفوظة 17 أبريل 2018 على موقع واي باك مشين. - Mehlhorn, Kurt; Sanders, Peter (2008). "Chapter 10. Shortest Paths" (PDF). Algorithms and Data Structures: The Basic Toolbox. Springer. doi:10.1007/978-3-540-77978-0. ISBN 978-3-540-77977-3. الوسيط
|CitationClass=تم تجاهله (مساعدة) - "Shortest Paths" (PDF). Department of Computer Science at Princeton University. مؤرشف من الأصل (PDF) في 25 نوفمبر 2011. اطلع عليه بتاريخ 24 أكتوبر 2019. الوسيط
|CitationClass=تم تجاهله (مساعدة)
- بوابة تقنية المعلومات
- بوابة خوارزميات
- بوابة علم الحاسوب
