خوارزمية تصنيفية

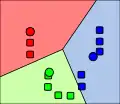
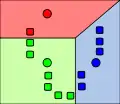
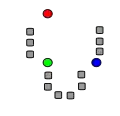
الخوارزمية التصنيفية (بالانجليزية: k-means clustering) هي طريقة لتكميم المتجهات، في الأصل في علم معالجة الإشارة والتي اشتهر استخدامها في تطبيقات التصنيف (cluster analysis) خلال عملية التنقيب في البيانات. الهدف من هذه الخوارزمية هو تقسيم عدد من العناصر (بيانات n) إلى عدد k من الأقسام والتي فيها ينضوي كل عنصر إلى القسم ذي النقطة المركزية الأقرب (المتوسط)، حيث تمثل النقطة المركزية الأساس الذي يتم عليه تقسيم البيانات وتصنيفها ولهذا أتت التسمية k-means clustering. نتيجة التصنيف هي القسمة إلى مناطق فورونية.

مقالة مفصلة: مخطط فورونوي

المشكلة تكمن في صعوبة الحساب، بمعنى صعوبة الوصول إلى نتيجة يتم على أساسها تضمين عنصر ما إلى قسم معين. وبرغم التشابه مع خوارزمية تعظيم التوقع (expectation-maximization algorithm EMA)، إلا أن ال k-means لا تُنتج أشكال مختلفة للبيانات المُجزئة كما تفعل ذلك الأولى (EMA).

الوصف

نأخذ العناصر المعطاة (x1, x2, …, xn) ، حيث كل عنصر يمثل متجها بُعده d. بعد تطبيق الخوارزمية على العناصر فيتم تقسيمها حسب التشابه بينها إلى عدد (k ≤ n) k من الأجزاء S: S = {S1, S2, …, Sk} بحيث يؤخذ القيمة الدنيا لمجموع التربيع بين كل عنصر وبين النقاط المركزية والتي عددها k (within-cluster sum of squares (WCSS)). العلاقة الرياضية تُعطى كالآتي:

{\underset {\mathbf {S} }{\operatorname {arg\,min} }}\sum _{i=1}^{k}\sum _{\mathbf {x} \in S_{i}}\left\|\mathbf {x} -{\boldsymbol {\mu }}_{i}\right\|^{2}

حيث μ_i هي متوسط العناصر في الجزء S_i.

التاريخ

أول من استخدم مصطلح ال "k-means" كان جيمس ماكوين في عام 1967 [1] بيدَ أن الفكرة خلف هذا المصطلح ترجع إلى هوجو شتاين هاوس في عام 1957.[2] التطبيق الكلاسيكي للخوارزمية تم اقتراحه من قبل ستوارت لويد في عام 1957 كتقنية تطبيقية للتضمين الرقمي، إلا أن النشر الأول لم يتم حتى عام [3] 1982.
في عام 1965 نشر E.W.Forgy نفس الطريقة، ولهذا يتم تسمية الخوارزمية أحيانا على إسمه.[4] تطوير اضافي على الخوارزمية تم نشرها من قِبَل هارتيجان ووونج في 1975/1979.[5]

التطبيق الخوارزمي

التطبيق الخوازمي لل k-means يستعمل تقنية تكرار التصنيف. ابتداءً من نقاط عشوائية للمراكز m1(1),…,mk(1) يمر التطبيق في الخطوتين التاليتين:[6]

تصنيف أولي

في هذه الخطوة يتم تصنيف كل عنصر إلى إحدى النقاط المركزية وفق نتيجة المسافة الإقليدية (WCSS) والتي تُعبر عن المتوسط الأقرب للنقاط. هذا يعني قسمة العناصر إلى مناطق فورونية، ويعطى رياضياً بالعلاقة الآتية:

S_{i}^{(t)}={\big \{}x_{p}:{\big \|}x_{p}-m_{i}^{(t)}{\big \|}^{2}\leq {\big \|}x_{p}-m_{j}^{(t)}{\big \|}^{2}\ \forall j,1\leq j\leq k{\big \}},

حيث كل عنصر $x_{p}$ يتم دمجه إلى منطقة مركزية $S^{(t)}$ واحدة بالتحديد.

تحديث المراكز

في هذه الخطوة يتم حساب النقاط المركزية من جديد بحيث تكون المراكز المحدثة للقطع (clusters) الجديدة.

m_{i}^{(t+1)}={\frac {1}{|S_{i}^{(t)}|}}\sum _{x_{j}\in S_{i}^{(t)}}x_{j}

حساب النقاط المركزية الجيدية (الأنسب) يعني أيضا تقليل الحساب المتوسطي بين العناصر ومراكزها (WCSS) داخل كل منطقة.

معرض صور

المصادر

MacQueen, J. B. (1967). Some Methods for classification and Analysis of Multivariate Observations. Proceedings of 5th Berkeley Symposium on Mathematical Statistics and Probability. 1. University of California Press. صفحات 281–297. MR = 0214227 0214227. Zbl = complete&q = an:0214.46201 0214.46201. مؤرشف من الأصل في 29 أكتوبر 2019. اطلع عليه بتاريخ 07 أبريل 2009. الوسيط |CitationClass= تم تجاهله (مساعدة)
Steinhaus, H. (1957). "Sur la division des corps matériels en parties". Bull. Acad. Polon. Sci. (باللغة الفرنسية). 4 (12): 801–804. MR = 0090073 0090073. Zbl = complete&q = an:0079.16403 0079.16403. الوسيط |CitationClass= تم تجاهله (مساعدة)
Lloyd, S. P. (1957). "Least square quantization in PCM". Bell Telephone Laboratories Paper. الوسيط |CitationClass= تم تجاهله (مساعدة) Published in journal much later: Lloyd., S. P. (1982). "Least squares quantization in PCM" (PDF). IEEE Transactions on Information Theory. 28 (2): 129–137. doi:10.1109/TIT.1982.1056489. مؤرشف من الأصل (PDF) في 17 يونيو 2009. اطلع عليه بتاريخ 15 أبريل 2009. الوسيط |CitationClass= تم تجاهله (مساعدة)
E.W. Forgy (1965). "Cluster analysis of multivariate data: efficiency versus interpretability of classifications". Biometrics. 21: 768–769. JSTOR 2528559. الوسيط |CitationClass= تم تجاهله (مساعدة)
J.A. Hartigan (1975). Clustering algorithms. John Wiley & Sons, Inc. الوسيط |CitationClass= تم تجاهله (مساعدة)
MacKay, David (2003). "Chapter 20. An Example Inference Task: Clustering". Information Theory, Inference and Learning Algorithms. Cambridge University Press. صفحات 284–292. ISBN 0-521-64298-1. MR = 2012999 2012999. مؤرشف من الأصل (PDF) في 08 مايو 2017. الوسيط |CitationClass= تم تجاهله (مساعدة)

بوابة تقنية المعلومات
بوابة علم الحاسوب

خوارزمية تصنيفية في المشاريع الشقيقة

صور وملفات صوتية من كومنز

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.

[macqueen1967-1] MacQueen, J. B. (1967). Some Methods for classification and Analysis of Multivariate Observations. Proceedings of 5th Berkeley Symposium on Mathematical Statistics and Probability. 1. University of California Press. صفحات 281–297. MR = 0214227 0214227. Zbl = complete&q = an:0214.46201 0214.46201. مؤرشف من الأصل في 29 أكتوبر 2019. اطلع عليه بتاريخ 07 أبريل 2009. الوسيط |CitationClass= تم تجاهله (مساعدة)

[2] Steinhaus, H. (1957). "Sur la division des corps matériels en parties". Bull. Acad. Polon. Sci. (باللغة الفرنسية). 4 (12): 801–804. MR = 0090073 0090073. Zbl = complete&q = an:0079.16403 0079.16403. الوسيط |CitationClass= تم تجاهله (مساعدة)

[lloyd1957-3] Lloyd, S. P. (1957). "Least square quantization in PCM". Bell Telephone Laboratories Paper. الوسيط |CitationClass= تم تجاهله (مساعدة) Published in journal much later: Lloyd., S. P. (1982). "Least squares quantization in PCM" (PDF). IEEE Transactions on Information Theory. 28 (2): 129–137. doi:10.1109/TIT.1982.1056489. مؤرشف من الأصل (PDF) في 17 يونيو 2009. اطلع عليه بتاريخ 15 أبريل 2009. الوسيط |CitationClass= تم تجاهله (مساعدة)

[forgy65-4] E.W. Forgy (1965). "Cluster analysis of multivariate data: efficiency versus interpretability of classifications". Biometrics. 21: 768–769. JSTOR 2528559. الوسيط |CitationClass= تم تجاهله (مساعدة)

[hartigan1975-5] J.A. Hartigan (1975). Clustering algorithms. John Wiley & Sons, Inc. الوسيط |CitationClass= تم تجاهله (مساعدة)

[6] MacKay, David (2003). "Chapter 20. An Example Inference Task: Clustering". Information Theory, Inference and Learning Algorithms. Cambridge University Press. صفحات 284–292. ISBN 0-521-64298-1. MR = 2012999 2012999. مؤرشف من الأصل (PDF) في 08 مايو 2017. الوسيط |CitationClass= تم تجاهله (مساعدة)