حالة مستقرة

في ديناميكا حرارية يكون نظام في حالة مستقرة إذا لم يتغير مع الزمن .

كما يتضح من الحالات في الشكل فليست الحالة المستقرة ثابتا رياضيا:

${\displaystyle |\Psi (t)\rangle =e^{-iE_{\Psi }t/\hbar }|\Psi (0)\rangle }$

وإنما تظهر جميع خواص الحالة المستقرة كثوابت . وعلى سبيل المثال، إذا كانت ${\displaystyle |\Psi (t)\rangle }$ تمثل دالة موجية لجسيم يتحرك على محور واحد (${\displaystyle \Psi (x,t)}$ يكون احتمال وجود الجسيم عند النقطة x :

${\displaystyle |\Psi (x,t)|^{2}=\left|e^{-iE_{\Psi }t/\hbar }\Psi (x,0)\right|^{2}=\left|e^{-iE_{\Psi }t/\hbar }\right|^{2}\left|\Psi (x,0)\right|^{2}=\left|\Psi (x,0)\right|^{2}}$

وهي دالة لا تعتمد على الزمن t .

ثلاثة حلول لمعادلة شرودنجر المعتمدة على الزمن في حالة الهزاز التوافقي. إلى اليسار : الجزء الحقيق (أزرق) والجزء التخيلي (أحمر) للدالة الموجية. وإلى اليمين : احتمال وجود الجسيم عند نقطة معينة . يمثل الطابقان العلويان حالتين للحالة المستقرة، أما المربعان السفليان فيبنان التطابق الكمومي للحالة ${\displaystyle \psi _{N}\equiv (\psi _{0}+\psi _{1})/{\sqrt {2}}}$ وهي ليست حالة مستقرة (فهي تتغير مع الزمن) . وتوضح الصور علي اليمين، لماذا نسمي الحالات المستقرة بأنها "مستقرة" أو " أرضية".

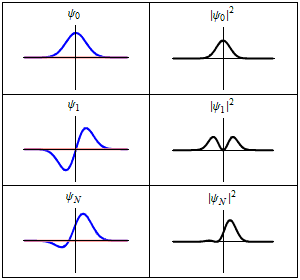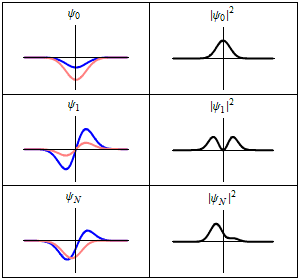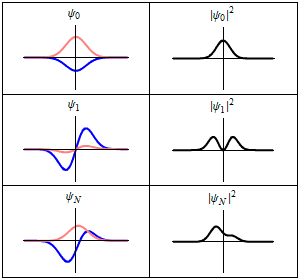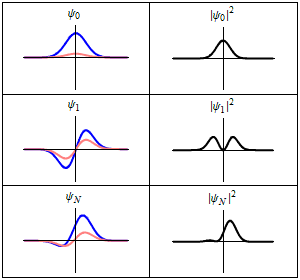
وقد صاغ هايزنبرج فيما يسمى صورة هايزنبرج صياغة رياضية بديلة لميكانيكا الكم، وفيها تكون الحالة المستقرة عبارة عن ثابتا رياضيا بالفعل ولا يتغير مع الزمن.

وكما ذكرنا أعلاه فتلك المعادلات تفترض أن معادلة هاميلتون لا تتغير مع الزمن. وهذا يعني أن الحالات المستقرة تكون فقط مستقرة عندما يكون باقي النظام ثابتا ومستقرا في نفس الوقت . وعلى سبيل المثال، فإن الإلكترون في ذرة الهيدروجين يكون في حالة مستقرة (رغم دورانه المستمر في مدار حول النواة) ، ولكن عندما تتفاعل ذرة الهيدروجين مع ذرة أخرى، عندئذ فإن الإلكترون سوف يغادر مداره ويصبح في حالة إثارة.

• رقم كم.
• حالة إثارة
• انفطار (فيزياء)

• بوابة كيمياء فيزيائية
• بوابة الفيزياء
• بوابة الكيمياء
• بوابة ميكانيكا الكم