توزيع منتظم

في نظرية الاحتمالات والإحصاء، يعرّف التوزيع المنتظم المستمر على أنّه توزيع احتمالي يقضي لكل متغير عشوائي تابع له بأن يستطيع الحصول على قيم محصورة في فترة مستمرّة واحدة ووحيدة على محور الأعداد الصحيحة، بحيث يكون الاحتمال بحصول المتغير على قيم في أي فترة جزئية محتواة في هذه الفترة يكون الاحتمال متساويًا، بشرط أن تكون جميع الفترات الجزئية متساوية الطول.[1] بما معناه أنّ دالة الكثافة الاحتمالية لهذا التوزيع ثابتة في الفترة المذكورة، ومساوية لصفر خارج تلك الفترة. غالبًا ما يتم التنويه إلى المتغير العشوائي الذي ينتمي إلى هذه العائلة بالطريقة التالية: ${\displaystyle U\!\left(a,b\right)}$ ، بحيث أنّ a هي القيمة الصغرى في الفترة وb هي القيمة العظمى هناك.

التوزيع المنتظم

دالة الكثافة الاحتمالية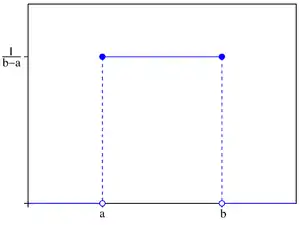
دالة التوزيع التراكمي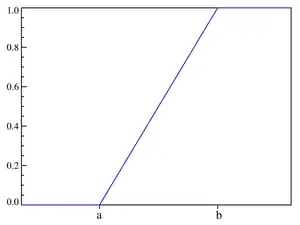
المؤشرات	${\displaystyle -\infty <a<b<\infty }$
الدعم	${\displaystyle \left[a,b\right]}$
د۔ك۔ح۔	${\displaystyle {\begin{cases}{\frac {1}{b-a}}\quad a\leq x\leq b\\0\quad \quad x<a,x>b\end{cases}}}$
د۔ت۔ت	${\displaystyle {\begin{cases}0\quad \quad x<a\\{\frac {x-a}{b-a}}\quad a\leq x\leq b\\1\quad \quad x>b\end{cases}}}$
المتوسط الحسابي	${\displaystyle {\tfrac {a+b}{2}}}$
الوسيط الحسابي	${\displaystyle {\tfrac {a+b}{2}}}$
المنوال	أي عدد في الفترة ${\displaystyle \left[a,b\right]}$
التباين	${\displaystyle {\tfrac {\left(b-a\right)^{2}}{12}}}$
التجانف	0
التفرطح	${\displaystyle -{\tfrac {6}{5}}}$
الاعتلاج	${\displaystyle \ln \left(b-a\right)}$
د۔م۔ع	${\displaystyle M_{X}(t)={\frac {e^{tb}-e^{ta}}{t\left(b-a\right)}}}$
الدالة المميزة	${\displaystyle \phi _{X}(t)={\frac {e^{itb}-e^{ita}}{it\left(b-a\right)}}}$
معلومات فيشر	{{{معلومات فيشر}}}