تفرطح
التفرطح (بالإنجليزية: Kurtosis) ويسمى أيضا بمعامل التفرطح أو معامل التسطيح أو درجة التقوس أو الكورتوسيس، هو مؤشر لقياس درجة تحدب أو تقوس دالة التوزيع الاحتمالي لمتغير عشوائي حقيقي. هو، إلى جانب التجانف، من أهم معالم أشكال توزيع المتغيرات العشوائية، ويمكن من وصف شكل توزيع الاحتمالات في جوار القيمة المتوقعة.[1]
تسميته الشائعة كورتوسيس مستنبطة من الإغريقية القديمة (κύρτωσις) وتعني الانحناءة أو التقوس.[2] أول من قام بتعريفه هو كارل بيرسون في القرن 19.[3]
تعريف
التفرطح الغير مُعيَّر
باعتبار متغير عشوائي حقيقي بمتوسط وانحراف معياري ، معامل التفرطح للمتغير هو العزم من الرتبة الرابعة للتحويلة المعيارية ل :[3]
وهو يساوي : مع العزم من الرتبة للمتغير .
التفرطح المعير
ويسمى أيضا بالتفرطح بإفراط (بالإنجليزية:Excess Kurtosis) ويقضي بطرح 3 من التفرطح الغير معير: .
هذه الصيغة هي الأكثر استعمالا بين الإحصائيين، وتعرف بتفرطح فيشر، وأيضا في البرامج الإحصائية (التي تقوم بحساب قيمة مقدر بدون انحياز ل ). يعزى هذا التفضيل إلى كون قيمة التفرطح بالنسبة لتوزيع طبيعي تساوي 3، وبذلك تعتبر حالة التوزيع الطبيعي كنوع من المعايرة القياسية لكل التوزيعات الأخرى.[3] [4][5]
مقدر بدون انحياز
المقدر الأكثر استخداما لحساب هو:
بحيث باعتبار و هما المقدران، بدون انحياز، على التوالي للقيمة المتوقعة وتباين المتغير .
مجال تغير التفرطح
باعتبار مربع التحويلة الموسطة المختزلة ل : ،
فالقيمة المتوقعة ل تساوي وتباينه يساوي
وبحكم أن التباين قيمة موجبة، نستنتج أن:
- و
للتفرطح إذا عتبة دنيا بينما ليست له عتبة عليا. العتبة الدنيا () تتحقق في حالة توزيع بيرنولي .
أشكال التفرطح
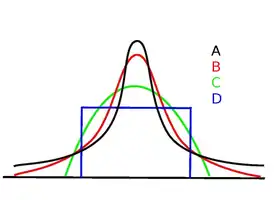
- ، تفرطح متوسط (Mesokurtic): كما في حالة التوزيع الطبيعي.
- ، تفرطح رفيع (Leptokurtic): المميز للتوزيعات الاحتمالية التي تكون قمة منخناها رفيعة.
- تفرطح مسطح (Platykurtic): تكون قمة منحنى التوزيع آيلة للتسطيح.
مراجع
- "Statistiques descriptives". مؤرشف من الأصل في 24 ديسمبر 2019. الوسيط
|CitationClass=تم تجاهله (مساعدة) - "Paramètres de forme". مؤرشف من الأصل في 24 ديسمبر 2019. الوسيط
|CitationClass=تم تجاهله (مساعدة) - "Kurtosis". مؤرشف من الأصل في 23 ديسمبر 2019. الوسيط
|CitationClass=تم تجاهله (مساعدة) - "Skewness et kurtosis des pr´evisions de bénéfice : Impact sur les rendements" (PDF). مؤرشف من الأصل (PDF) في 29 مارس 2017. الوسيط
|CitationClass=تم تجاهله (مساعدة) - "La distribution normale". مؤرشف من الأصل في 12 أكتوبر 2018. الوسيط
|CitationClass=تم تجاهله (مساعدة)
- بوابة إحصاء
 صور وملفات صوتية من كومنز
صور وملفات صوتية من كومنز
