تناظر انعكاسي

يقال عن شكل بأنه ذو تناظر انعكاسي (بالإنجليزية: Reflection Symmetry)‏ إذا كان ينطبق على نفسه تماما عندما يُثى حول خط مار في وسطه.[1][2][3] يسمى الخط المار في وسطه خط التناطر. في حالة شكل مستوي (ذو بعدين) يستعمل اصلاحي تناظر انعكاسي أو تناظر خطي. وفي حالة جسم ذي ثلاثة أبعاد فيعبر عن ذلك بمستوي التناظر (انظر الشكل). يمكن تصور مستوي التناظر بوضع مرآة في مكانه.

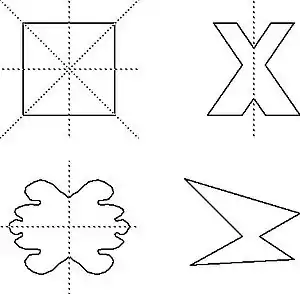
بعض الأشكال وما لها من محاور تناطر ، الشكل تحت إلى اليمين ليس له محور تناظر.

تناظر انعكاسي للصورة ، أما إذا كان الشكل مجسما فيكون له مستوي تناظر.

أمثلة

للمربع أربعة محاور تناظر. أما المستطيل فله محوري تناظر. كما أن للمعين أيضا محوري تناظر.
للمكعب ثلاثة مستويات تناظر، واحد رأسي في اتجاه الرؤية مارا بمنتصف المكعب، ومستوى تناظر ثاني رأسي عمودي على اتجاه الرؤية ومارا بمنتصف المكعب، ومستوي تناظر ثالث أفقي يقسمه إلى نصفين متساووين.
للدائرة عدد لا نهائي من محاور التناظر (جميعها مارا بالمركز).
للكرة أيضا عدد لا نهائي من محاور التناظر. كما أن لها عدد لا نهائي من مستويات التناظر.
لمتوازي المستطيلات ثلاثة مستويات تناظر (عمودية على بعضها البعض).

مراجع

Tavernor, Robert (1998). On Alberti and the Art of Building. Yale University Press. صفحات 102–106. ISBN 978-0-300-07615-8. مؤرشف من الأصل في 26 يوليو 2018. More accurate surveys indicate that the facade lacks a precise symmetry, but there can be little doubt that Alberti intended the composition of number and geometry to be regarded as perfect. The facade fits within a square of 60 Florentine braccia الوسيط |CitationClass= تم تجاهله (مساعدة)
Finnerty, John R. (2005). "Did internal transport, rather than directed locomotion, favor the evolution of bilateral symmetry in animals?" (PDF). BioEssays. 27: 1174–1180. doi:10.1002/bies.20299. PMID 16237677. مؤرشف من الأصل (PDF) في 2 يوليو 2019. اطلع عليه بتاريخ أغسطس 2020. الوسيط |CitationClass= تم تجاهله (مساعدة); تحقق من التاريخ في: |تاريخ الوصول= (مساعدة)
Valentine, James W. "Bilateria". AccessScience. مؤرشف من الأصل في 18 يناير 2008. اطلع عليه بتاريخ 29 مايو 2013. الوسيط |CitationClass= تم تجاهله (مساعدة)

انظر أيضا

بوابة علوم
بوابة الفيزياء
بوابة ميكانيكا الكم
بوابة فنون
بوابة رياضيات
بوابة هندسة رياضية

في كومنز صور وملفات عن: تناظر انعكاسي

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.

[1] Tavernor, Robert (1998). On Alberti and the Art of Building. Yale University Press. صفحات 102–106. ISBN 978-0-300-07615-8. مؤرشف من الأصل في 26 يوليو 2018. More accurate surveys indicate that the facade lacks a precise symmetry, but there can be little doubt that Alberti intended the composition of number and geometry to be regarded as perfect. The facade fits within a square of 60 Florentine braccia الوسيط |CitationClass= تم تجاهله (مساعدة)

[2] Finnerty, John R. (2005). "Did internal transport, rather than directed locomotion, favor the evolution of bilateral symmetry in animals?" (PDF). BioEssays. 27: 1174–1180. doi:10.1002/bies.20299. PMID 16237677. مؤرشف من الأصل (PDF) في 2 يوليو 2019. اطلع عليه بتاريخ أغسطس 2020. الوسيط |CitationClass= تم تجاهله (مساعدة); تحقق من التاريخ في: |تاريخ الوصول= (مساعدة)

[3] Valentine, James W. "Bilateria". AccessScience. مؤرشف من الأصل في 18 يناير 2008. اطلع عليه بتاريخ 29 مايو 2013. الوسيط |CitationClass= تم تجاهله (مساعدة)