تكامل مونت كارلو
في الرياضيات، تكامل مونت كارلو (بالإنجليزية: Monte Carlo integration) هي طريقة تكامل العددي تستخدم لإجراء التكامل العددي لدالة ما عن طريق أخذ قيم عشوائية من مجال الدالة.[1]
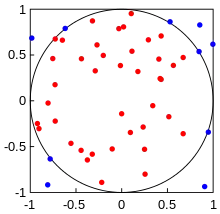
An illustration of Monte Carlo integration. In this example, the domain D is the inner circle and the domain E is the square. Because the square's area (4) can be easily calculated, the area of the circle (π*12) can be estimated by the ratio (0.8) of the points inside the circle (40) to the total number of points (50), yielding an approximation for the circle's area of 4*0.8 = 3.2 ≈ π*12.
انظر أيضا
مراجع
- "معلومات عن تكامل مونت كارلو على موقع academic.microsoft.com". academic.microsoft.com. مؤرشف من الأصل في 27 أكتوبر 2020. الوسيط
|CitationClass=تم تجاهله (مساعدة)
وصلات خارجية
- بوابة رياضيات
- بوابة إحصاء
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.
