تصنيف دمجي
تصنيف دمجي هي إحدى خوارزميات التصنيف أو ترتيب مجموعة من عناصر الرقمية تصاعديا، طورها العالم الألماني فون نيومان، تعتمد هذه الخوارزمية على مبدء "فرق تسد" (بالإنجليزية: divide and conquer)، عدد الخطوات اللازمة للخوارزمية لإنجاز المعالجة على مجموعة من مدخلات تقاس بـ N*Log N.[1][2][3]
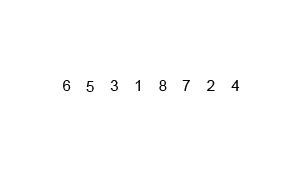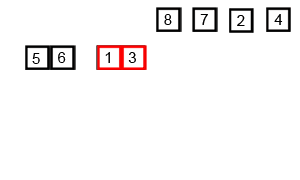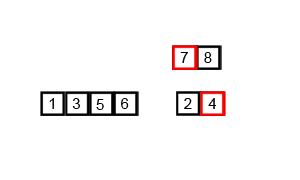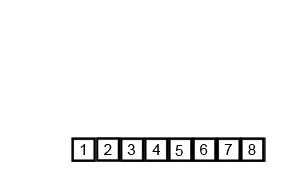
مثال للتصنيف الدمجي.
خطوات الخوارزمية مفهوم خوارزمية التصنيف الدمجي يقوم على خطوات التالية:
- إذا كانت المصفوفة تحتوي على عنصر واحد أو أقل فإن المصفوفه مصنفة، لأنها تحتوي على عنصر واحد وبالتالي هو مصنف.
- قْسِّم كل مصفوفة غير مصنفة - أي تحتوي على أكثر من عنصر - إلى مصفوفتين.
- أعد ترتيب كل مصفوفة بطريقة الاستدعاء الذاتي recursively.
- ادمج كل مصفوتين (التي تم تريبها) إلى مصفوفة واحدة.
تعتمد الخوارزمية بشكل أساسي على مفهومين رئيسيين :
- المفهوم الأول : هو أن المصفوفات التي تحتوي على أقل عناصر يمكن ترتيبها بشكل أسرع وتحتاج إلى خطوات أقل.
- المفهوم الثاني : هو عملية دمج المصفوفات الصغيرة التي تحتوي على عناصر قليلة المرتبة لتشكيل مصفوفات أكبر مرتبة أيضا.
تطبيق من الأعلى إلى الأسفل (Top-down)
function merge_sort(list m)
// if list size is 1, consider it sorted and return it
if length(m) <= 1
return m
// else list size is > 1, so split the list into two sublists
var list left, right
var integer middle = length(m) / 2
for each x in m up to middle
add x to left
for each x in m after or equal middle
add x to right
// recursively call merge_sort() to further split each sublist
// until sublist size is 1
left = merge_sort(left)
right = merge_sort(right)
// merge the sublists returned from prior calls to merge_sort()
// and return the resulting merged sublist
return merge(left, right)
في هذا المثال، الدالة merge تدمج المجموعتين الجزئيتين اليسرى واليمنى:
function merge(left, right) var list result while length(left) > 0 or length(right) > 0 if length(left) > 0 and length(right) > 0 if first(left) <= first(right) append first(left) to result left = rest(left) else append first(right) to result right = rest(right) else if length(left) > 0 append first(left) to result left = rest(left) else if length(right) > 0 append first(right) to result right = rest(right) end while return result
تطبيق من الأسفل إلى الأعلى (Bottom-up)
/* array A[] has the items to sort; array B[] is a work array */
BottomUpSort(int n, array A[n], array B[n])
{
int width;
/* each 1-element run in A is already "sorted". */
/* Make successively longer sorted runs of length 2, 4, 8, 16... until whole array is sorted */
for (width = 1; width < n; width = 2 * width)
{
int i;
/* array A is full of runs of length width */
for (i = 0; i < n; i = i + 2 * width)
{
/* merge two runs: A[i:i+width-1] and A[i+width:i+2*width-1] to B[] */
/* or copy A[i:n-1] to B[] ( if(i+width >= n) ) */
BottomUpMerge(A, i, min(i+width, n), min(i+2*width, n), B);
}
/* now work array B is full of runs of length 2*width */
/* copy array B to array A for next iteration */
/* a more efficient implementation would swap the roles of A and B */
CopyArray(A, B, n);
/* now array A is full of runs of length 2*width */
}
}
BottomUpMerge(array A[], int iLeft, int iRight, int iEnd, array B[])
{
int i0 = iLeft;
int i1 = iRight;
int j;
/* while there are elements in the left or right lists */
for (j = iLeft; j < iEnd; j++)
{
/* if left list head exists and is <= existing right list head */
if (i0 < iRight && (i1 >= iEnd || A[i0] <= A[i1]))
{
B[j] = A[i0];
i0 = i0 + 1;
}
else
{
B[j] = A[i1];
i1 = i1 + 1;
}
}
}
مراجع
- "liboctave/util/oct-sort.cc". Mercurial repository of Octave source code. Lines 23-25 of the initial comment block. مؤرشف من الأصل في 6 فبراير 2019. اطلع عليه بتاريخ 18 فبراير 2013.
Code stolen in large part from Python's, listobject.c, which itself had no license header. However, thanks to Tim Peters for the parts of the code I ripped-off.
الوسيط|CitationClass=تم تجاهله (مساعدة) - Geffert, Viliam; Katajainen, Jyrki; Pasanen, Tomi (2000). "Asymptotically efficient in-place merging". Theoretical Computer Science. 237: 159–181. doi:10.1016/S0304-3975(98)00162-5. الوسيط
|CitationClass=تم تجاهله (مساعدة) - V. J. Duvanenko, "Parallel Merge Sort", Dr. Dobb's Journal, March 2011 نسخة محفوظة 14 سبتمبر 2011 على موقع واي باك مشين.
- بوابة خوارزميات
- بوابة علم الحاسوب
في كومنز صور وملفات عن: تصنيف دمجي
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.
