تربيع غاوسي

في التحليل العددي، تعد قاعدة التربيع تقريبًا للتكامل المحدد للدالة، وعادة ما يتم ذكرها كمجموع مرجح لقيم الدالة عند نقاط محددة داخل مجال التكامل. قاعدة التربيع الغاوسية متعدد النقاط (n نقطة)، المسماة باسم كارل فريدريش غاوس،[1] هي قاعدة تربيعية تم إنشاؤها لتحقيق نتيجة دقيقة لكثيرة الحدود من الدرجة $2 n - 1$ أو أقل من خلال اختيار مناسب للعقد $x i$ والأوزان $w i$ لـ i = 1،…، n. طوِّرت الصيغة الحديثة باستخدام كثيرات الحدود المتعامدة من قبل كارل غوستاف جاكوبي 1826. يتم أخذ المجال الأكثر شيوعًا للتكامل لمثل هذه القاعدة على النحو [−1 ، 1]، [2]لذلك تم ذكر القاعدة على أنها

\int _{-1}^{1}f(x)\,dx\approx \sum _{i=1}^{n}w_{i}f(x_{i}),

تحتاج هذه المقالة إلى الاستشهاد بمصادر إضافية لتحسين وثوقيتها. فضلاً ساهم في تطوير هذه المقالة بإضافة استشهادات من مصادر موثوقة. من الممكن التشكيك بالمعلومات غير المنسوبة إلى مصدر وإزالتها.

هل تقصد تكامل غاوسي

مقارنة بين التربيع الغاوسي ثنائي النقاط والتربيع شبه المنحرفي. المنحنى الأزرق هو كثير الحدود معادلته

{\textstyle y(x)=7x^{3}-8x^{2}-3x+3}

، التي تكاملها في

[-1, 1]

يساوي

2 ⁄ 3

. تُرجع قاعدة شبه المنحرف تكامل الخط البرتقالي المتقطع، مساوٍ لـ

{\textstyle y(-1)+y(1)=-10}

. تُرجع قاعدة التربيع الغاوسية المكونة من نقطتين تكامل المنحنى الأسود المتقطع، مساوٍ لـ

{\textstyle y\left(-{\sqrt {\frac {1}{3}}}\right)+y\left({\sqrt {\frac {1}{3}}}\right)={\frac {2}{3}}}

. هذه النتيجة دقيقة، حيث أن المنطقة الخضراء لها نفس مساحة مجموع المناطق الحمراء.

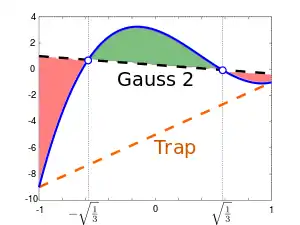
والتي تكون مضبوطة بالنسبة لكثيرات الحدود من الدرجة $2 n - 1$ أو أقل. تُعرف هذه القاعدة المضبوطة باسم قاعدة غاوس-ليجاندر التربيعية. ستكون قاعدة التربيع فقط تقريبًا دقيقًا للتكامل أعلاه إذا تم تقريب $f (x)$ بشكل جيد بواسطة كثير الحدود من الدرجة $2 n - 1$ أو أقل في $[-1, 1]$ .

مراجع

Methodus nova integralium valores per approximationem inveniendi. In: Comm. Soc. Sci. Göttingen Math. Band 3, 1815, S. 29–76, Gallica, datiert 1814, auch in Werke, Band 3, 1876, S. 163–196. نسخة محفوظة 12 يوليو 2019 على موقع واي باك مشين.
ريتشارد ل; فايرس, ج دوغلاس (2014-08-19). التحليل العددي. العبيكان للنشر. ISBN 978-603-503-506-4. مؤرشف من الأصل في 18 يوليو 2020. الوسيط |CitationClass= تم تجاهله (مساعدة)

انظر أيضا

صيغة أويلر-ماكلورين

بوابة رياضيات
بوابة تحليل رياضي

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.

[1] Methodus nova integralium valores per approximationem inveniendi. In: Comm. Soc. Sci. Göttingen Math. Band 3, 1815, S. 29–76, Gallica, datiert 1814, auch in Werke, Band 3, 1876, S. 163–196. نسخة محفوظة 12 يوليو 2019 على موقع واي باك مشين.

[2] ريتشارد ل; فايرس, ج دوغلاس (2014-08-19). التحليل العددي. العبيكان للنشر. ISBN 978-603-503-506-4. مؤرشف من الأصل في 18 يوليو 2020. الوسيط |CitationClass= تم تجاهله (مساعدة)