انطباق

في الهندسة الرياضية، تنطبق نقطتان إذا وقعتا في المكان نفسه.[1] ويُقال أيضاً لشكلين أو خطين مُستقيمين أنهما منطبقين إذا كانت كل نقطة في أحدهما منطبقة على نقطة من الشكل الآخر.

حالات وعلاقات الكائنات الهندسية فيما بينها
تسامُتٌ تلاقٍ
توازٍ تعامد
تنصيف انطباقٌ
دَائريَّةٌ تماس
السعي نحو اللانهاية انعدامٌ
مُخالَفَةٌ اشتراك في مستوى
زاوية منعدمة رأسها مركز المستوى الإحداثي.
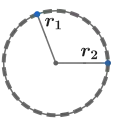
دائرتان منطبقتان، لهما نفس نصف القطر ونفس نقطة المركز

أمثلة

حدوث الانطباق في بعض الأشكال والمُستقيمات يُؤدي إلى ظهور حالات خاصَّة منها. مثل:

  • يُعبَّر عن تقاطع مستقيمات في نقطة واحدة بانطباق نقاط تقاطع كل مُستقيمين منهما مثنى مثنى على بعضها بعضاً.
  • تتكون الزاوية المنعدمة من انطباق شعاعي الزاوية على بعضهما بعضاً.[2][3]
  • عندما تنطبق النقاطُ المُكوِّنةُ لمُستقيمِ أويلر (مراكز المثلث) يتحول المثلث الأصلي إلى مثلثٌ متطابق الأضلاع.
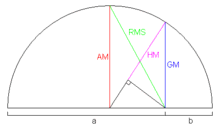
الإنشاء الهندسي لمتباينات الأوساط.

متباينات الأوساط

تُبرهن متباينات الأوساط بالإنشاء الهندسي داخل نصف دائرة، وتحصل حالة المساواة عندما تنطبق النقطة المتحركة على القطر على مركز الدائرة.

انظر أيضاً

مراجع
  1. Cormen, Thomas H.; Leiserson, Charles E.; Rivest, Ronald L.; Stein, Clifford (31 July 2009). Introduction to Algorithms. MIT Press. صفحة 1042. ISBN 978-0-262-25810-4. مؤرشف من الأصل في 2 يناير 2020. الوسيط |CitationClass= تم تجاهله (مساعدة)
  2. Team, Almaany. "تعريف و معنى الزّاوية المنعدمة بالعربي في معجم المعاني الجامع، المعجم الوسيط ،اللغة العربية المعاصر - معجم عربي عربي - صفحة 1". www.almaany.com (باللغة الإنجليزية). مؤرشف من الأصل في 13 ديسمبر 2019. اطلع عليه بتاريخ 28 سبتمبر 2018. الوسيط |CitationClass= تم تجاهله (مساعدة)
  3. "Medida de ángulos". recursostic.educacion.es. مؤرشف من الأصل في 5 سبتمبر 2017. اطلع عليه بتاريخ 28 سبتمبر 2018. الوسيط |CitationClass= تم تجاهله (مساعدة)
    • بوابة رياضيات
    • بوابة هندسة رياضية
    This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.