البرهان على أن باي عدد غير كسري
درس العدد π منذ العصور القديمة، كما هو الحال أيضا بالنسبة إلى مفهوم الأعداد غير الجذرية.[1] عدد لا جذري هو كل عدد لا يمكن كتابته على شكل كسر a/b حيث a عدد صحيح وحيث b عدد صحيح لا يساوي الصفر.
في القرن الثامن عشر، برهن يوهان هاينغيش لامبرت على كون π عددا غير جذري.
برهان لامبرت
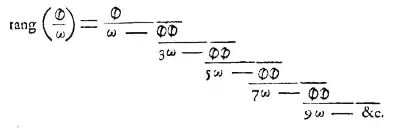
صيغة لامبرت كما جاءت في الصفحة 288 في أطروحته "أطروحة حول بعض الخصائص المهمة للكميات المتسامية والدائرية واللوغارتمية", Mémoires de الأكاديمية الملكية للعلوم في برلين (1768), 265–322.
في عام 1761، أثبت يوهان هاينغيش لامبرت أن π عدد غير جذري؛ وذلك من خلال البرهان أولا على أن الكسر المستمر أسفله يساوي ظل x:
ثم البرهان على أنه إذا كان x عددا جذريا، فإن دالة الظل تكون غير جذرية.
وبما أن tan(π/4)=1 عدد جذري، هذا يعني أن π/4، وبالأخص π، عدد غير جذري.
من أجل هذا البرهان، قد تستعمل متسلسلة تايلور على دالتي الجيب والجيب التمام.
برهان نيفن
افترض نيفن أن π عادد جذري، مما مكنه من كتابة π=a/b حيث a و b عددان صحيحان. بدون فقدان للتعميم، افترض أن هذين العددين موجبان.
for each x ∈ ℝ let
مراجع
- "معلومات عن البرهان على أن باي عدد غير كسري على موقع academic.microsoft.com". academic.microsoft.com. مؤرشف من الأصل في 30 أكتوبر 2020. الوسيط
|CitationClass=تم تجاهله (مساعدة)
- بوابة رياضيات
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.
