ارتفاع (مثلث)
في الهندسة الرياضية، الارتفاع في المثلث هو الخط العمودي النازل من إحدى زوايا المثلث إلى الضلع المقابل لهذه الزاوية أو امتداد هذا الضلع.[1][2][3]
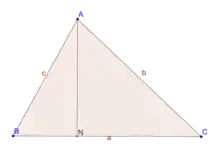
و يعرف هذا الضلع المقابل لهذه الزاوية بـقاعدة الارتفاع، بينما تسمى نقطة التقاطع بين الارتفاع و قاعدته بـقدم الارتفاع.
حالات الارتفاع
للارتفاع في المثلث ثلاث حالات إما أن يسقط داخل المثلث أو يكون ضلعاً فيه أو أن يسقط خارجه على امتداد قاعدة الارتفاع.
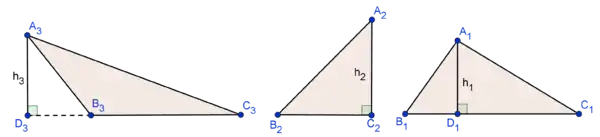
خصائص الارتفاع
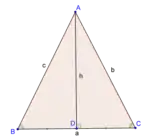

- تعطى مساحة المثلث بالقانون:
المساحة = ½ الارتفاع × قاعدة الارتفاع.
- إذا كان الارتفاع ضلعاً في مثلث ما فإن هذا المثلث قائم الزاوية في قدم الارتفاع.
- في أي مثلث ثلاثة ارتفاعات تتقاطع في نقطة واحدة تعرف بـملتقى الارتفاعات ( تستخدم مبرهنة سيفا لاثبات ما سبق).
- الارتفاع الساقط على قاعدة المثلث المتساوي الساقين ينصفها عند قدم الارتفاع (من تطابق المثلثين ADC و ADB ).
- في أي مثلث ABC، زواياه A,B,C و أطوال أضلاعه a,b,c يعطى طول الارتفاع الساقط على BC بالقانون:
حساب طول الارتفاع
الصيغة الأولى
إذا كان الارتفاع h يقسم الوتر في المثلث ABC القائم في C إلى p و g فإن طول الارتفاع يعطى بالقانون:
البرهان: إذا كان المثلث ABC قائم في C و CH ارتفاع قدمه H فإن المثلثان HBC و HCA متشابهان و من التشابه ينتج:
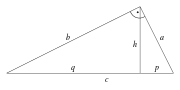
و هو المطلوب.
الصيغة الثانية
إذا كانت a,b,c أطوال أضلاع المثلث ABC القائم في C فإن الارتفاع الساقط على AB يعطى بالقانون:
البرهان:
إذا كان المثلث ABC قائم في C و CH ارتفاع قدمه H فإن:
AC ارتفاع مساحة المثلث = ½ BC × AC
كذلك CH ارتفاع مساحة المثلث = ½ AB × CH
و هو المطلوب.
في المثلث المتساوي الأضلاع
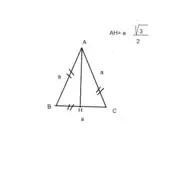
إذا كان a طول ضلع المثلث المتطابق الأضلاع فإن طول الارتفاع فيه يعطى بالقانون:
البرهان:
ِِإذا كان ABC مثلث متطابق الأضلاع طول ضلعه a و AH ارتفاع فيه قدمه H فإن:
H منتصف BC ( من خواص الارتفاع السابق ذكرها ).
بتطبيق مبرهنة فيثاغورس على AHC
و هو المطلوب.
ملتقى الارتفاعات
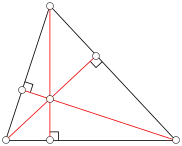
ملتقى الارتفاعات (orthocentre), أو "المركز القائم" لمثلث هو نقطة تقاطع ارتفاعات المثلث.
تتقاطع الارتفاعات في مثلث في نقطة واحدة ولذلك يكفي لإيجاد نقطة ملتقى الارتفاعت رسم ارتفاعين فقط في أي مثلث.
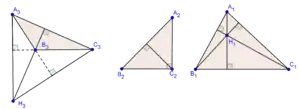
كما هو الحال في الارتفاعات فإن لملتقى الارتفاعات ثلاث حالات إما أن تكون داخل المثلث أو تكون رأساً في المثلث أو تكون خارجة عن المثلث.
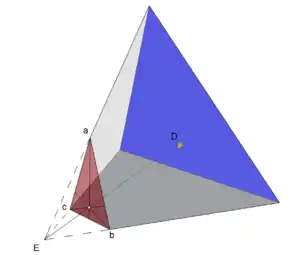
في الهندسة الفراغية، عندما يمثل المثلث مقطع قائم لهرم ثلاثي، فإن ملتقى ارتفاعات هذا المثلث يقع على المستقيم العمود من رأس الهرم المقطوع على الوجه المقابل له.
مراجع
- "Archived copy". مؤرشف من الأصل في 19 أبريل 2012. اطلع عليه بتاريخ 19 أبريل 2012. الوسيط
|CitationClass=تم تجاهله (مساعدة)صيانة CS1: الأرشيف كعنوان (link) - "Orthocenter of a triangle" نسخة محفوظة 03 أكتوبر 2017 على موقع واي باك مشين. [وصلة مكسورة]
- William H. Barker, Roger Howe (2007). "§ VI.2: The classical coincidences". Continuous symmetry: from Euclid to Klein. American Mathematical Society. صفحة 292. ISBN 0-8218-3900-4. مؤرشف من الأصل في 25 يناير 2020. الوسيط
|CitationClass=تم تجاهله (مساعدة)
- بوابة رياضيات
- بوابة هندسة رياضية
