إكمال المربع
إكمال المربع هي عملية لتحويل الدالة التربيعية من الشكل
إلى الشكل
ومصطلح "constant" يعني أنه قيمة ثابتة ولا يعتمد على x. والجزء داخل القوسين يكون على صورة (x + constant) ، بمعنى أن:
تحولت إلى
بقيم معينة لكلا من h و k.
استخدامات طريقة إكمال المربع:
- حل المعادلات التربيعية
- رسم المعادلات التربيعية
- حساب التكامل في التفاضل والتكامل مثل تكامل جاوس.
- إيجاد تحويل لابلاس.
ويعد إكمال المربع من العمليات الأساسية في الرياضيات، ويتم استخدامها -حتى بدون الإشارة إليها- في الحسابات التي تحتوي على معادلات تربيعية. كما أن هذه الطريقة تستخدم لاستنتاج طريقة حل المعادلات التربيعية باستخدام المميز.
مقدمة
تمهيد
يوجد صيغة بسيطة في علم الجبر لحساب مربع كثيرة الحدود ذات الإسمين
مثال:
ففي أي مربع كامل العدد p يكون دائما هو نصف معامل x ، ويكون الحد الثابت هو مربع p أي يساوي p2.
مثال بسيط
في كثيرة الحدود التربيعية التالية:
نجد أنها ليست مربعا كاملا، لأن 28 لا تساوي مربع 5 .
بينما يمكننا أن نضع الدالة الأصلية على صورة: (مربع كامل + ثابت) كما يلي:
وهذا ما يسمى إكمال المربع.
وصف عام
لأي كثيرة حدود واحدية المدخل (أي معامل x يساوي 1) من الدرجة الثانية (أي تربيعية) على الصورة:
يمكن أن نكون 'مربعا كاملا' له نفس الحدين الأولين
وهذا المربع الكامل يختلف عن الدالة الأصلية في الحد الثابت فقط. ويمكن أن نكتب
حيث k هو ثابت. وهذه العملية تسمى إكمال المربع. ومثالا لذلك:
غير واحدية المدخل
لأي كثيرة حدود غير واحدية المدخل (معامل x لا يساوي 1) على الصورة:
يمكن أن نقوم باتخاذ a معاملا مشتركا، ثم نكمل المربع بالطريقة السابقة.
مثال:
ومعنى هذا أننا يمكن أن نكتب أي كثيرة حدود تربيعية على الصورة
صيغة عامة
يمكن كتابة صيغة عامة لعملية إكمال المربع كالتالي:[1]
حيث:
- حالة خاصة عندما a=1:
حيث:
- وفي حالة المصفوفات (يراعى ترتيب ضرب المصفوفات):
حيث:
ويجب أن تكون المصفوفة متماثلة (أي مدور المصفوفة يساوي نفس المصفوفة).
أما لو كانت المصفوفة غير متماثلة فإن صيغة حساب و يتم تغييرها إلى الصورة العامة:
- .
و
- .
علاقته بالرسم
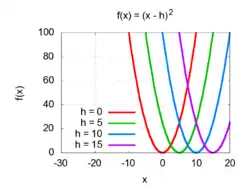
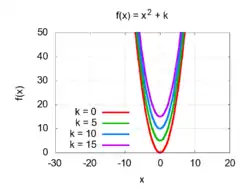
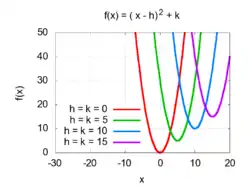
رسم أي دالة تربيعية هو قطع مكافئ في مستوى xy. فالدالة التربيعية على صورة:
الأرقام h و k تمثل إحداثيات نقطة رأس القطع المكافئ. وتمثل h الإحداثي x لمحور التماثل، بينما تمثل k القيمة الصغرى ( أو العظمى إذا كانت a < 0 ) للدالة التربيعية.
ويمكن القول أن رسم منحنى الدالة التربيعية ƒ(x) = x2 هو قطع مكافئ، رأسه عند نقطة الأصل (0, 0).
بينما رسم منحنى الدالة ƒ(x − h) = (x − h)2 هو قطع مكافئ تمت إزاحته جهة اليمين بالقيمة h ورأسه هي (h, 0) كما هو مبين بالشكل.
ورسم منحنى الدالة ƒ(x) + k = x2 + k هو قطع مكافئ تمت إزاحته لأعلى بالقيمة k، ورأسه هي نقطة كما هو مبين بالشكل الثاني.
ويمكن جمع الإزاحتين الأفقية (يمين أو يسار) والرأسية (أعلى أو أسفل) فالدالة ƒ(x − h) + k = (x − h)2 + k
هي قطع مكافئ مزاح لليمين بالقيمة h، ومزاح لأعلى بالقيمة k، ورأسه عند النقطة (h, k)، كما هو مبين بالشكل الثالث.
حل المعادلات التربيعية
تستخدم طريقة إكمال المربع لحل المعادلات التربيعية، ومثال ذلك:
الخطوة الأولى هي إكمال المربع:
ثم نحل الحد المربع:
وبالتالي إما
إذن
ويمكن تطبيق ذلك لأي معادلة تربيعية. وعندما يكون معامل x2 لا يساوي 1 تكون الخطوة الأولى هي قسمة المعادلة على هذا المعامل. انظر المثال التالي:
الجذور غير النسبية أو المركبة
يمكن استخدام إكمال المربع للحصول على جذور الدالة التربيعية حتى لو كانت تلك الجذور هي جذور غير نسبية أو جذور مركبة. مثال للجذور غير النسبية:
بإكمال المربع نحصل على
وبالتالي
إذن إما
إذن
وعادةً تكتب على الصورة:
ومثال للمعادلات ذات الجذور المركبة:
حيث الرمز i يساوي
تطبيقات أخرى
التكامل
يمكن استخدام إكمال المربع لحساب التكامل كالتالي:
باستخدام قواعد التكامل
مثال:
بإكمال المربع للمقام نحصل على:
وبالتالي يمكن إجراء التكامل بالتعويض.
u = x + 3,
الذي يُنتج
الأعداد المركبة
العلاقة التالية
حيث z وb هما عدادان مركبان، و هما العددان المرافقان لهما على الترتيب، و c هو عدد حقيقي.
باستخدام القاعدة
يمكن إعادة كتابة العلاقة السابقة على الصورة
والتي يتضح أنها كمية حقيقة
مثال آخر المعادلة التالية:
حيث a و b و c و x و y هي أعداد حقيقية، و a > 0 و b > 0, يمكن صياغتها على صورة مربع القيمة المطلقة لعدد مركب كالتالي: نفرض
إذن
وبالتالي
المنظور الهندسي
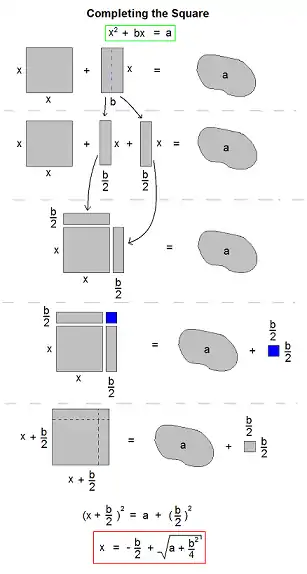
لإكمال المربع للمعادلة
حيث أن x2 تمثل مساحة مربع طول ضلعه x،
وbx تمثل مساحة مستطيل ضلعاه هما b و x،
وبالتالي فإن عملية إكمال المربع يمكن اعتبارها إكمال المستطيلات لنصل إلى مربع.
إذا حاولنا إنشاء مربعا كبيرا مكون من (المربع x2 ) و(المستطيل bx ) معا، سنجد أن هناك ركنا ناقصا يحتاج إلى إكماله. الحد الذي يتم إضافته إلى المعادلة يمثل مساحة هذا الركن الذي نحتاجه لإكمال المربع، ومن هنا جاءت التسمية إكمال المربع
إكمال المربع بطريقة مختلفة
كما رأينا سابقا فقد أضفنا الحد الثالث v 2 إلى المعادلة
لنحصل على مربع. لكن هناك حالات أخرى نقوم فيها بإضافة الحد الثاني (أو الأوسط) بحيث يكون إما (2uv) أو (2uv-) إلى المعادلة
لنحصل على مربع على الصورة:
أو
مثال: مجموع رقم موجب ومقلوبه
إذا أردنا إيجاد حاصل جمع أي رقم موجب مع مقلوبه يمكننا استخدام هذه الطريقة:
واضح أن مجموع أي رقم موجب مع مقلوبه يكون دائما أكبر من أو يساوي 2 لأن مربع أي قيمة حقيقية يكون أكبر من أو يساوي الصفر.
مثال: تحليل معادلة بسيطة
عند تحليل المعادلة التالية
نجد أنها على صورة
وبالتالي يمكن استخدام الحد الأوسط على صورة
فسوف نحصل على
وهذا هو فرق بين مربعين يتم تحليله كالتالي:
السطر الأخير تم كتابته لتبدو كثيرة الحدود في الصورة المألوفة حسب الترتيب التنازلي لدرجة المتغير x.
مصادر
- Algebra 1, Glencoe, ISBN 0-07-825083-8, pages 539–544
- Algebra 2, Saxon, ISBN 0-939798-62-X, pages 214–214, 241–242, 256–257, 398–401
مراجع
- Narasimhan, Revathi (2008). Precalculus: Building Concepts and Connections. Cengage Learning. صفحات 133–134. ISBN 0-618-41301-4. الوسيط
|CitationClass=تم تجاهله (مساعدة), Section Formula for the Vertex of a Quadratic Function, page 133–134, figure 2.4.8