معيار التشفير المتقدم

معيار التشفير المتقدم
Advanced Encryption Standard
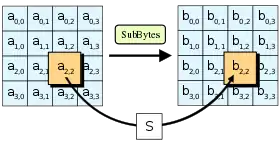	خطوة SubBytes، وهي واحدة من الخطوات الأربعة لدورة معيار التشفير المتقدم
معلومات عامة
اختصار	AES
المطورون	فنسنت ريجمين وجوان دايمن
تاريخ النشر	1998
اشتقت من	سكوير
اشتق منها	كريبتون ، أنوبيس ، جراند كرو
معلومات التشفير
طول المفتاح	128 أو 192 أو 256 بت
طول المجموعة	128 بت
البنية	شبكة الاستبدال والتبديل
عدد الدورات	10 أو 12 أو 14 (اعتمادًا على طول المفتاح)
أفضل تحليل شيفرة عام
تحليل الشيفرة	قد يؤدي هجوم المفاتيح ذات الصلة إلى تقسيم ما يصل إلى 9 دورات من 256 بت معيار التشفير المتقدم

معيار التشفير المتقدم[1][2] (بالإنجليزية: Advanced Encryption Standard)‏ ويُدعى اختصارًا إيه إي إس (AES)، هو طريقة تشفير رسمية تبنتها NIST (المركز القومي للمعايير والتكنولوجيا وهو فرع في حكومة الولايات المتحدة).[3][4][5] هذه الخوارزمية لاقت قبولاً واسعاً في العالم إذ أنها تُعتبر طريقة آمنة للتشفير وذلك بسبب طول مفتاح التشفير. هذه الخوارزمية هي تطوير لافكار ظهرت في DES.

تاريخ

في عام 1997 بدأت NIST بالبحث عن بديل ل-DES وذلك لان DES كان يُعتبر بشكل واسع آنذاك انه غير آمن وذلك بسبب تطوير وسائل متطورة لكسر هذه الوسيلة، وقد كانت التسعينات نهاية DES حيث أنه Wiener في بداية التسعينيات اعلن عن آلة بقيمة 1000000 دولار لكسر DES في 3.5 ساعات فقط ! كل هذا ساهم بالاساس في الإعلان عن إصدار معيار تشفير اقوى، وقد كان إحدى أهداف هذا البحث هو الإعلان عن بديل يُستخدم بشكل عام ولا يقتصر على الجيش، ولاجل هذا دعت كل المتخصصين في علم التعمية لتقديم اقتراحاتهم وكانت الشروط كالتالي :

يجب أن يتم تعريف AES علانية
يجب أن يكون AES خوارزمية تشفير كُتل متماثل(symmetric block cipher) .
يجب تصميم AES بحيث أن طول المفتاح يمكن أن نطوله حسب الحاجة .
يمكن برمجة AES بواسطة البرمجيات والعتاد الصلب للحاسوب (software and hardware)
يجب على ِAES ان يكون مُتاح مجانا أو مُتاح بتناسق مع سياسة ANSI لبراءة الاختراعات
الخوارزميات التي تتماشى مع النقاط السابقة سيتم اختبارها بناء على المعايير الآتية :
1. الأمان: أي مدى مقاومته للأساليب المعروفة لكسر خوارزميات التشفير.
2. جودة الحساب: أي قياس الزمن اللازم للتشفير وكلما كان اقل كانت الخوارزمية أكثر جودة .
3. مُتطلبات الذاكرة: أي سعة الذاكرة الإلكترونية المستخدمة في تنفيذ الخوارزمية.
4. ملاءمة الخوارزمية للبرمجيات والعتاد الصلب للحاسوب.
5. بساطة الخوارزمية.
6. مرونة الخوارزمية.
7. متطلبات الترخيص.

ولاحقا تم تحديد طول (المفتاح، الكتلة) الذي من المفترض ان يقدمها AES وهي : (256,128),(192,128),(128,128).

والمسابقة كانت على مرحلتين في المرحلة الأولى تقدمت 15 خوارزمية وفي عام 1999 تم اختيار 5 خوارزميات للتصفيات وهي :

MARS
RC6
RIJNDEAL
SERPENT
TWOFISH

وفي تشرين أول من عام 2000 تم اختيار RIJNDEAL ليكون بديل DES وقد تم تغيير اسمه ل- AES وفي تشرين ثاني من عام 2001 أصبح معيارا رسميا (FIPS 197 ). مُخترعي هذا المعيار هما دايمن ورامين(Daemen and Rijmen )

رايندول

رايندول هو خوارزمية تشفير كتل وهو يدعم أطوال مفاتيح وأطوال نصوص متعددة . مفتاح التشفير k هو مصفوفة ذات أبعاد $4\times N_{k}$ (اي طول المفتاح هو $4\cdot N_{k}$ بايت ) :

${\underline {k}}={\begin{pmatrix}k_{0,0}&k_{0,1}&\cdots &k_{0,N_{k-1}}\\k_{1,0}&k_{1,1}&\cdots &k_{1,N_{k-1}}\\k_{2,0}&k_{2,1}&\cdots &k_{2,N_{k-1}}\\k_{3,0}&k_{3,1}&\cdots &k_{3,N_{k-1}}\end{pmatrix}}$

حيث كل $k_{i,j}$ يمكن اعتباره :

8 بِْتْ أو 1 بَايْتْ اي انه عدد في المجموعة ${\mathcal {Z}}_{2,8}$
عدد صحيح في المجموعة ${\mathcal {Z}}_{256}$

طول المفتاح في خوارزمية رايندول يمكن أن يكون $N_{k}=4,6,8\ (128,192,256)$ بايت .

قراءة مفتاح التشفير من المصفوفة تكون حسب كل عامود من اليسار إلى اليمين أي :

{\underline {k}}=(k_{0,0},k_{1,0},k_{2,0},k_{3,0},\cdots ,k_{0,N_{k-1}},k_{1,N_{k-1}},k_{2,N_{k-1}},k_{3,N_{k-1}})

الكتلة أو النص الذي نريد تشفيره ${\underline {x}}$ هو مصفوفة ذات اطوال $4\times N_{b}$ (اي طول المفتاح هو $4\cdot N_{b}$ بايت ) :

${\underline {x}}={\begin{pmatrix}x_{0,0}&x_{0,1}&\cdots &x_{0,N_{b-1}}\\x_{1,0}&x_{1,1}&\cdots &x_{1,N_{b-1}}\\x_{2,0}&x_{2,1}&\cdots &x_{2,N_{b-1}}\\x_{3,0}&x_{3,1}&\cdots &x_{3,N_{b-1}}\end{pmatrix}}$

حيث كل $x_{i,j}$ يمكن اعتباره :

8 بِْتْ أو 1 بَايْتْ اي انه عدد في المجموعة ${\mathcal {Z}}_{2,8}$
عدد صحيح في المجموعة ${\mathcal {Z}}_{256}$

الكتلة في خوارزمية رايندول يمكن أن تكون $N_{b}=4,6,8\ (128,192,256)$ بايت .

قراءة الكتلة من المصفوفة تكون حسب كل عامود من اليسار إلى اليمين أي :

{\underline {x}}=(x_{0,0},x_{1,0},x_{2,0},x_{3,0},\cdots ,x_{0,N_{k-1}},x_{1,N_{k-1}},x_{2,N_{k-1}},x_{3,N_{k-1}})

وضعية رايندال ${\boldsymbol {\omega }}$ هو المصفوفة :

${\underline {\boldsymbol {\omega }}}={\begin{pmatrix}{\boldsymbol {\omega }}_{0,0}&{\boldsymbol {\omega }}_{0,1}&\cdots &{\boldsymbol {\omega }}_{0,N_{b-1}}\\{\boldsymbol {\omega }}_{1,0}&{\boldsymbol {\omega }}_{1,1}&\cdots &{\boldsymbol {\omega }}_{1,N_{b-1}}\\{\boldsymbol {\omega }}_{2,0}&{\boldsymbol {\omega }}_{2,1}&\cdots &{\boldsymbol {\omega }}_{2,N_{b-1}}\\{\boldsymbol {\omega }}_{3,0}&{\boldsymbol {\omega }}_{3,1}&\cdots &{\boldsymbol {\omega }}_{3,N_{b-1}}\end{pmatrix}}$

حيث كل ${\boldsymbol {\omega }}_{i,j}$ هو عدد صحيح في ${\mathcal {Z}}_{256}$ .

رايندول هو تركيب تحويلات (Transformations) على وضعيات رايندول وهذه التحويلات سنسميها الدورات (iterations) أي : $RIJ({\underline {x}})={\underline {y}}=(T_{N_{r}}\circ T_{N_{r-1}}\circ \cdots \circ T_{N_{1}}\circ T_{N_{0}})$

كل $T_{i}:{\boldsymbol {\omega }}\to {\boldsymbol {\omega }}$ أي أن المجال والمدى هو وضعيات رايندول ,

عدد الدورات ( $N_{r}$ )يتعلق بطول المفتاح ( $N_{k}$ ) وطول النص ( $N_{b}$ ) :

عدد دورات رايندول ( $N_{r}$ )
	$N_{b}=4$	$N_{b}=6$	$N_{b}=8$
$N_{k}=4$	10	12	14
$N_{k}=6$	12	12	14
$N_{k}=8$	14	14	14

الدورة الأولى $T_{0}$ هو XOR بين النص (الوضعية الأولى ) وبين مفتاح التشفير اي :

$T_{0}(x)={\begin{pmatrix}k_{0,0}&k_{0,1}&\cdots &k_{0,N_{k-1}}\\k_{1,0}&k_{1,1}&\cdots &k_{1,N_{k-1}}\\k_{2,0}&k_{2,1}&\cdots &k_{2,N_{k-1}}\\k_{3,0}&k_{3,1}&\cdots &k_{3,N_{k-1}}\end{pmatrix}}\oplus {\begin{pmatrix}x_{0,0}&x_{0,1}&\cdots &x_{0,N_{k-1}}\\x_{1,0}&x_{1,1}&\cdots &x_{1,N_{k-1}}\\x_{2,0}&x_{2,1}&\cdots &x_{2,N_{k-1}}\\x_{3,0}&x_{3,1}&\cdots &x_{3,N_{k-1}}\end{pmatrix}}$

الدورات التي تأتي بعد هذا سوف تُعنى بتحويل الوضعية الحالية، ولتتم هذا الخوارزمية تفعل هذا في مراحل :

عملية الخلط الخطية - التحويلات هي ShiftRow و- MixColumn ;
العملية غير الخطية - وهي التحويلة ByteSub ;
عملية إضافة المفتاح - التحويلة AddRoundKey .

حتى نُظهر المُعمى يكفي ان نقلب التحويلات أي : $RIJ^{-1}({\underline {y}})={\underline {x}}=(T_{N_{0}}^{-1}\circ T_{N_{1}}^{-1}\circ \cdots \circ T_{N_{r-1}}^{-1}\circ T_{N_{r}}^{-1})$

عملية الاستبدال

عملية استبدال البايت هي مصفوفة S ثابتة دائما (اي عندما نريد التشفير عملية الاستبدال تتم من خلال هذا الصندوق دوما ) والاستبدال يتم وفقا للمصفوفة التالية :

word8 S[256] = {

99, 124, 119, 123, 242, 107, 111, 197, 48, 1, 103, 43, 254, 215, 171, 118,

202, 130, 201, 125, 250, 89, 71, 240, 173, 212, 162, 175, 156, 164, 114, 192,

183, 253, 147, 38, 54, 63, 247, 204, 52, 165, 229, 241, 113, 216, 49, 21,

4, 199, 35, 195, 24, 150, 5, 154, 7, 18, 128, 226, 235, 39, 178, 117,

9, 131, 44, 26, 27, 110, 90, 160, 82, 59, 214, 179, 41, 227, 47, 132,

83, 209, 0, 237, 32, 252, 177, 91, 106, 203, 190, 57, 74, 76, 88, 207,

208, 239, 170, 251, 67, 77, 51, 133, 69, 249, 2, 127, 80, 60, 159, 168,

81, 163, 64, 143, 146, 157, 56, 245, 188, 182, 218, 33, 16, 255, 243, 210,

205, 12, 19, 236, 95, 151, 68, 23, 196, 167, 126, 61, 100, 93, 25, 115,

96, 129, 79, 220, 34, 42, 144, 136, 70, 238, 184, 20, 222, 94, 11, 219,

224, 50, 58, 10, 73, 6, 36, 92, 194, 211, 172, 98, 145, 149, 228, 121,

231, 200, 55, 109, 141, 213, 78, 169, 108, 86, 244, 234, 101, 122, 174, 8,

186, 120, 37, 46, 28, 166, 180, 198, 232, 221, 116, 31, 75, 189, 139, 138,

112, 62, 181, 102, 72, 3, 246, 14, 97, 53, 87, 185, 134, 193, 29, 158,

225, 248, 152, 17, 105, 217, 142, 148, 155, 30, 135, 233, 206, 85, 40, 223,

140, 161, 137, 13, 191, 230, 66, 104, 65, 153, 45, 15, 176, 84, 187, 22

};

مثال : إذا كان العدد الذي نريد استبداله هو 0x19 (حسب نظام العد الستة عشري) حينها يتم استبداله كالتالي : نذهب للسطر الأول العامود التاسع والناتج هو 0x4d أو 212(حسب القاعدة 10 ) كما هو مبين في الصورة :

عملية ازاحة السطر

وهي عملية تزيح اسطر الوضعية بإزاحة دائرية، وهي تزيح السطر ال-i : i ازاحات يساراً,

$SR:\omega ={\begin{pmatrix}\omega _{0,0}&\omega _{0,1}&\omega _{0,2}&\omega _{0,3}\\\omega _{1,0}&\omega _{1,1}&\omega _{1,2}&\omega _{1,3}\\\omega _{2,0}&\omega _{2,1}&\omega _{2,2}&\omega _{2,3}\\\omega _{3,0}&\omega _{3,1}&\omega _{3,2}&\omega _{3,3}\end{pmatrix}}\to {\begin{pmatrix}\omega _{0,0}&\omega _{0,1}&\omega _{0,2}&\omega _{0,3}\\\omega _{1,1}&\omega _{1,2}&\omega _{1,3}&\omega _{1,0}\\\omega _{2,2}&\omega _{2,3}&\omega _{2,0}&\omega _{2,1}\\\omega _{3,3}&\omega _{3,0}&\omega _{3,1}&\omega _{3,2}\end{pmatrix}}$

خلط العواميد

وهي عملية خلط خطية للعواميد، بمعنى انها تتم بواسطة مصفوفة، وهذه العملية مُعرفة بواسطة عمليات في $GF(2^{8})$ . اي انه لكل عامود

${\begin{bmatrix}s_{0}'\\s_{1}'\\s_{2}'\\s_{3}'\\\end{bmatrix}}={\begin{bmatrix}2&3&1&1\\1&2&3&1\\1&1&2&3\\3&1&1&2\end{bmatrix}}{\begin{bmatrix}s_{0}\\s_{1}\\s_{2}\\s_{3}\end{bmatrix}}$

الحقل $GF(2^{8})$ مبني على متعدد الحدود $x^{8}+x^{4}+x^{3}+x+1$ .

طريقة أخرى لتنفيذ العملية هي :

${\begin{bmatrix}b_{0}\\b_{1}\\b_{2}\\b_{3}\\\end{bmatrix}}={\begin{bmatrix}f(a_{0},a_{1},a_{2},a_{3})\\f(a_{1},a_{2},a_{3},a_{0})\\f(a_{2},a_{3},a_{0},a_{1})\\f(a_{3},a_{0},a_{1},a_{2})\end{bmatrix}}$

في حين أَنَّ : $f(a_{0},a_{1},a_{2},a_{3})=(a_{1}\oplus a_{2}\oplus a_{3})\oplus g((a_{0}\oplus a_{1})<<1)$ و- $g(x)={\begin{cases}x\oplus 11B_{x},&{\mbox{if }}x\land 100_{x}{\mbox{ true}}\\x,&{\mbox{else}}\end{cases}}$

مقلوب هذه التحويلة هو أيضا خطي وهو مشابه جدا للعملية نفسها ما عدا اننا نكتب d مكان f :

$d_{1}(a_{0},a_{1},a_{2},a_{3})=a_{0}\oplus a_{1}\oplus a_{2}\oplus a_{3}$

$d_{2}(a_{0},a_{1},a_{2},a_{3})=g(d_{1}(a_{0},a_{1},a_{2},a_{3})<<1)\oplus (a_{0}\oplus a_{2})$

$d_{3}(a_{0},a_{1},a_{2},a_{3})=g(d_{2}(a_{0},a_{1},a_{2},a_{3})<<1)\oplus (a0\oplus a1)$

$d(a_{0},a_{1},a_{2},a_{3})=g(d_{3}(a_{0},a_{1},a_{2},a_{3})<<1)\oplus (a_{1}\oplus a_{2}\oplus a_{3})$

إضافة مفتاح الدورة

ببساطة هذه العملية تعمل التالي : تأخذ الوضعية الحالية وتعمل XOR مع مفتاح الدورة ( مفتاح الدورة لديه نفس طول الوضعية الحالية اي النص ) مفتاح الدورة نحسبه بواسطة خوارزمية إنتاج المفاتيح . إذا كانت الوضعية الحالية هي : $\omega$ ومفتاح الدورة هو $k$ حينها :

${\begin{pmatrix}k_{0,0}&k_{0,1}&k_{0,2}&k_{0,3}\\k_{1,0}&k_{1,1}&k_{1,2}&k_{1,3}\\k_{2,0}&k_{2,1}&k_{2,2}&k_{2,3}\\k_{3,0}&k_{3,1}&k_{3,2}&k_{3,3}\end{pmatrix}}\oplus {\begin{pmatrix}\omega _{0,0}&\omega _{0,1}&\omega _{0,2}&\omega _{0,3}\\\omega _{1,0}&\omega _{1,1}&\omega _{1,2}&\omega _{1,3}\\\omega _{2,0}&\omega _{2,1}&\omega _{2,2}&\omega _{2,3}\\\omega _{3,0}&\omega _{3,1}&\omega _{3,2}&\omega _{3,3}\end{pmatrix}}$

التشفير وفك التشفير

التشفير كالتالي :

أولا نضيف المفتاح الدورة الأول ( $K_{0}$ )
$N_{r}$ $\text{[math]}$ دورات في كل دورة :
1. عملية الاستبدال
2. ازاحة الاسطر
3. خلط الأعمدة (ما عدا الدورة الأخيرة)
4. إضافة مفتاح الدورة ( اي انه في الدورة $i$ نضيف المفتاح $K_{i}$ ) .

حتى نفك التشفير كما ذكرنا في البداية يجب قلب ترتيب عمليات التشفير حسب الترتيب .

خوارزمية إنتاج المفاتيح

وهي ضرورية لإنتاج مفتاح جديد من الذي استخدمناه سابقا ( لذا لن نستخدم نفس المفتاح مرتين ) والخوارزمية مدخلها مصفوفة بكبر $N_{k}$ كلمات (كل كلمة هي 32 بيت ) والخوارزمية تحسب مفتاح الدورة $N_{r}+1$ (الدورة القادمة),ليكن W مصفوفة كلمات وهو بكبر $W[4*(N_{r}+1)$ . حينها 4 الكلمات الأولى تصبح مفتاح الدورة الأولى و 4 الكلمات القادمة هي مفتاح الدورة الثانية وهكذا ... والخوارزمية هي كالتالي :

W[0..Nk-1] = key[*];
for i := Nk to 4*(Nr+1)-1 do {
temp = W[i-1]
if((i%Nk)==0)
temp = bytesubstitution(temp<<<8) ^ RCON[i/Nk];
if((Nk==8) & ((i%Nk)==4))
temp = bytesubstitution(temp);
W[i] = W[i-Nk] ^ temp;
}

()bytesubstitution هي تنفيذ للمصفوفة S ,
في حين ان RCON هو المصفوفة التالية :

word32 RCON[] = {

$01_{x},02_{x},04_{x},08_{x},10_{x},20_{x},40_{x},80_{x},$

$1b_{x},36_{x},6c_{x},d8_{x},ab_{x},4d_{x},9a_{x},2f_{x}$

} لاحظ ان هذه الاعداد هي قوى العدد 2 في الحقل $GF(2^{8})$

خواص الامان

لا يوجد صفة المُكمل كما في DES . اي انه $AES_{k}(x)\neq AES_{\overline {k}}({\overline {x}})$
امان الخوارزمية كله متعلق باختيار المصفوفة S وهي الجزء الوحيد في الخوازمية الذي ليس خطيا أو تآلفي حيث أنه : $S[i]+S[j]\neq S[i+j]$ , مثلا إذا كان S مصفوفة تآلفية حينها كل العملية كانت لتكون تآلفية وبالتالي ليس آمنا ويمكن كسره بسهولة .
أفضل الهجمات على هذه الخوارزمية وهي على 7 دورات من الخوارزمية تأخذ وقت $2^{110}$ عندما طول المفتاح هو 128 بيت، اما إذا طول المفتاح 256 بيت فأفضل الهجمات على 8 دورات هو $2^{204}$ , لا يوجد هجمات مع وقت أقصر من هذا . كما أنه لا يوجد هجوم فعال على كل الدورات بمعنى ان وقت اللازم لكسر كل الخوارزمية هو $2^{128}$ عندما طول المفتاح هو 128 بيت .
بالرغم من انه لا يوجد برهان على أن رايندول آمن ولكن الخوارزمية آمنة لكل أنواع الهجمات المعروفة وقد تم فحص فعالية هذه الهجمات على الخوارزمية وكلها بائت بالفشل حيث أنها لم تستطع ان تخفض الوقت اللازم لكسر الخوارزمية اي ان أفضل وقت للهجوم على الخوارزمية هو $2^{128}$ بهذه الوسائل .

هل AES دالة وحيدة الاتجاه؟

بشكل عام لا يوجد برهان على أنَّ AES هي دالة وحيدة الاتجاه ولا حتى انه غير قابل للكسر ! ولكن بشكل عام يُعتقد أنها غير قابلة للكسر ما يجعل منها مرشحة لتكون دالة وحيدة الاتجاه , ولكن حتى الآن يُمكن اعتبارها كذلك وذلك لان نسبة البيانات التي نستطيع الحصول على مقلوبها هو صغير جدا.

استخدامات

بما أنَّ AES هو خوارزمية تشفير لذا فان له كثير من الاستخدامات التي تضم حماية المستخدم عبر الانترنت لتصل إلى حماية وضمان البيانات في البنوك والمعامل كما أن ل-AES استخدامات في المجالات العسكرية، ان ما ضمن ان AES نافع في كل هذه التطبيقات هو عدم وجود طريقة فعالة لكسره، كما أن بعض أشهر البرامج والبروتوكلات تعتمد على مقاومة AES للهجمات الإلكترونية ومنها :

يستخدم AES في برامج (WINZIP) في حالة ان المُستخدم طلب تشفير البيانات بعد ضغطها .
يُستخدم في برتوكول TLS , وهو برتوكول لإنشاء اتصال آمن .
له كذلك استخدام في برتوكول IPsec وهو برتوكول لضمان الامان في اتصالات التي تعمل بواسطة IP عبر الانترنت .

انظر أيضًا

مصادر

"Al-Qamoos القاموس - English Arabic dictionary / قاموس إنجليزي عربي". www.alqamoos.org. مؤرشف من الأصل في 06 أغسطس 2018. اطلع عليه بتاريخ 6 أغسطس 2018. الوسيط |CitationClass= تم تجاهله (مساعدة); تحقق من التاريخ في: |تاريخ أرشيف= (مساعدة)
"ترجمة و معنى advanced encryption standard بالعربي في قاموس المعاني. قاموس عربي انجليزي مصطلحات صفحة 1". www.almaany.com. مؤرشف من الأصل في 06 أغسطس 2018. اطلع عليه بتاريخ 6 أغسطس 2018. الوسيط |CitationClass= تم تجاهله (مساعدة); تحقق من التاريخ في: |تاريخ أرشيف= (مساعدة)
Alex Biryukov; Orr Dunkelman; Nathan Keller; Dmitry Khovratovich; Adi Shamir (2009-08-19). "Key Recovery Attacks of Practical Complexity on AES Variants With Up To 10 Rounds". مؤرشف من الأصل في 28 يناير 2010. اطلع عليه بتاريخ 11 مارس 2010. الوسيط |CitationClass= تم تجاهله (مساعدة)
"Breaking AES-128 in realtime, no ciphertext required | Hacker News". News.ycombinator.com. مؤرشف من الأصل في 26 يناير 2018. اطلع عليه بتاريخ 23 ديسمبر 2012. الوسيط |CitationClass= تم تجاهله (مساعدة)
Cryptology ePrint Archive: Report 2009/317 نسخة محفوظة 25 يناير 2018 على موقع واي باك مشين.

بوابة رياضيات
بوابة تعمية

في كومنز صور وملفات عن: معيار التشفير المتقدم

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.

[1] "Al-Qamoos القاموس - English Arabic dictionary / قاموس إنجليزي عربي". www.alqamoos.org. مؤرشف من الأصل في 06 أغسطس 2018. اطلع عليه بتاريخ 6 أغسطس 2018. الوسيط |CitationClass= تم تجاهله (مساعدة); تحقق من التاريخ في: |تاريخ أرشيف= (مساعدة)

[2] "ترجمة و معنى advanced encryption standard بالعربي في قاموس المعاني. قاموس عربي انجليزي مصطلحات صفحة 1". www.almaany.com. مؤرشف من الأصل في 06 أغسطس 2018. اطلع عليه بتاريخ 6 أغسطس 2018. الوسيط |CitationClass= تم تجاهله (مساعدة); تحقق من التاريخ في: |تاريخ أرشيف= (مساعدة)

[3] Alex Biryukov; Orr Dunkelman; Nathan Keller; Dmitry Khovratovich; Adi Shamir (2009-08-19). "Key Recovery Attacks of Practical Complexity on AES Variants With Up To 10 Rounds". مؤرشف من الأصل في 28 يناير 2010. اطلع عليه بتاريخ 11 مارس 2010. الوسيط |CitationClass= تم تجاهله (مساعدة)

[4] "Breaking AES-128 in realtime, no ciphertext required | Hacker News". News.ycombinator.com. مؤرشف من الأصل في 26 يناير 2018. اطلع عليه بتاريخ 23 ديسمبر 2012. الوسيط |CitationClass= تم تجاهله (مساعدة)

[5] Cryptology ePrint Archive: Report 2009/317 نسخة محفوظة 25 يناير 2018 على موقع واي باك مشين.