مسألة الحصان
مسألة الحصان هي مسألة رياضية قديمة، أساسها تمرير قطعة الحصان؛ طبقا لقواعد لعبة الشطرنج؛ مرة واحدة فقط من كل خانة على رقعة تشمل عددا nxn من الخانات. يوضع الحصان في خانة ما، ثم يمرر على جميع الخانات الأخرى وعندما يكمل دورته تنجز قطعة الحصان العدد n²-1 في رقعة تشمل nxn من الخانات. بالنسبة للرقعة العادية (8x8) ينجز الحصان 63 نقلة لحل المسألة.

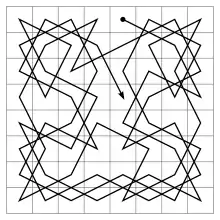
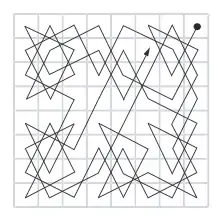
.png.webp)
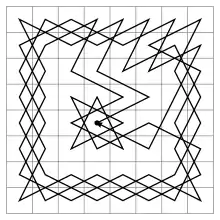
بحث العديد من الرياضيين لإيجاد حل لهذه المسألة الرياضية، بما في ذلك الرياضي أويلر. وجدت العديد من الحلول لهذه المسألة. لكن في الأمر الواقع لا أحد يعلم على وجه اليقين كم عدد الطرق المختلفة التي تحل المسألة. طور علماء الرياضيات نسخا أخرى من هذه المسألة وأضافوا بعض الاختلافات مثل أن تكون خانة الانطلاق هي نفسها خانة الوصول، وأطلق اسم "المسار المغلق " على حلول هذا التفريع من المسألة بينما أطلق اسم "دورة الحصان " على التفريع نفسه.
تاريخ المسألة
ترجع أصول هذه المسألة إلى قرون طويلة، ثم عرفت فيما بعد باسم "حصان أويلر".حوالي سنة 840 وجد المنظر ولاعب الشطرنج العربي العدلي الرومي حلا للمسألة.كما ذكرت في القرن التاسع في قصيدة شعرية اسمها" kavyalankara " للشاعر الهندي "Rudrata".و يعد بيار ريموند دو مونتمور هو أول من درس هذه المسألة في الغرب والتي نشرت سنة 1708 في كتاب «محاولة تحليل ألعاب الحظ».[1] وفي سنة 1759 استأنف عالم الرياضيات ليونهارد أويلر دراسة المسألة ونشر عنها بحثا سنة 1766 بعنوان «حل مسألة غريبة لا يظهر أنها خاضعة لأي تحليل» وكتب في رسالة إلى العالم الرياضي كريستيان غولدباخ:
| «تذكرت المسألة التي طرحت علي ذات يوم وكانت سببا في إيجاد أبحاث دقيقة تحتوي على تحليل عادي؛و كما يبدو؛لا يملك أي تطبيق يذكر. وأخيرا،وجدت طريقة واضحة للعثور على كم كبير من الحلول(لكن عددهم يبقى لا متناهيا)» |
كما نشر كوم الكسندر كوليني (1727 – 1806)؛ وهو سكرتير فولتير؛ سنة 1773 حلا في "المجلة الموسوعية".[2]
من بين ملايين الحلول، يوجد 122 مليون حل فقط للحالات التي تكون فيها خانة البدء هي خانة النهاية ويسمى كل منها بالمسار المغلق.تعد مسألة الحصان حالة خاصة من المسارات الهاملتونية في نظرية المخططات.
الحلول المختلفة
| 63 | 14 | 37 | 24 | 51 | 26 | 35 | 10 |
| 22 | 39 | 62 | 13 | 36 | 11 | 50 | 27 |
| 15 | 64 | 23 | 38 | 25 | 52 | 9 | 34 |
| 40 | 21 | 16 | 61 | 12 | 33 | 28 | 49 |
| 17 | 60 | 1 | 44 | 29 | 48 | 53 | 8 |
| 2 | 41 | 20 | 57 | 6 | 55 | 32 | 47 |
| 59 | 18 | 43 | 4 | 45 | 30 | 7 | 54 |
| 42 | 3 | 58 | 19 | 56 | 5 | 46 | 31 |
تنقسم الحلول إلى نوعين حسب شكل المسار: المسار المغلق، أي أن الحصان يبدء دورته وينهيها بنفس الخانة والمسار المفتوح، هي الحالة التي تبدأ فيها جولة الحصان من خانة وتنتهي في أخرى.
مصادر خارجية
- لتجريب هذه المسألة أو التمرن عليها:
- تحميل برنامج يساعد على حل هذا النوع من المسائل:
- موقع يدرس المسألة
- خوارزمية المسألة باللغة الإسبانية
مراجع
- "Essay d'analyse sur les jeux de hazard".
- "Journal Encyclopédique" [الفرنسية]
- بوابة رياضيات
- بوابة شطرنج
- بوابة علم الحاسوب
