مسألة أبولونيوس

في الهندسة الرياضية، مسألة أبولونيوس هي مسألة إنشاء دوائر مماسة لثلاث دوائر معلومة في المستوي. صاغ أبولونيوس بيرغا هذه المسألة وحلها في أحد أعماله التي ضاعت.

شرح مسألة أبولونيوس

أعطيت ثلاث دوائر مختلفة، يراد انشاء (بواسطة الرسم الرقمي) ثماني دوائر ماسة للدوائر المعطية. الاجراء الذي اعتمد يكمن في تحديد المحل الهندسي لجميع مراكز الدوائرالماسة كل زوج من الدوائر المعطية. كل زوج من الدوائر المعطية لة قطعين زائدين بخاصية ذلك المحل الهندسي. وبما ان الدوائر المعطية ثلاثة، فإن العدد الإجمالي للقطع الزائدة يكون ستة. النقاط المشتركة بين فروع كل ثلاثة قطع زائدة، تكون مراكز الدوائر الثماني المطلوبة.

الحلول الثمانية لمسألة أبولونيوس

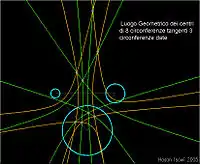
فإذا إفترضنا وجود ثلاث دوائر مختلفة، والمطلوب رسم (بواسطة الرسم الرقمي) ثمانية دوائر تمس هذه الدوائر المعطية. فالعمل الذي اعتمد يكمن في تحديد المحل الهندسي لجميع مراكز دوائر التماس، حيث كل زوج من الدوائر المعطاة له قطعين زائدين بخاصية ذلك المحل الهندسي. وبما ان الدوائر المعطاة ثلاثة، فإن العدد الإجمالي للقطوع الزائدة يكون ستة قطوع، والنقاط المشتركة بين فروع كل ثلاثة قطع زائدة، تكون مراكز الدوائر الثماني المطلوبة.

نلاحظ أنه إذا تلامست دائرتان في نقطة محددة فإنَّ نقطة التماس تقع على الخط المستقيم المار بمركزيهما، وممكن أن تتلامس الدائرتان من الداخل أو من الخارج، ويحدث ذلك عندما تقع أحد الدائرتين داخل الدائرة الأخرى، فإذا تلامسا خارجيًا كانت المسافة بين مركزيهما مساوية لمجموع نصفي قطريهما. أمَّا إذا تلامسا داخليًا: فإنَّ المسافة بين مركزيهما تساوي الفرق بين نصفي قطريهما.[1]

بشكل عام فإن ثلاث دوائر متباعدة لها ثمانية دوائر مختلفة تمسها. وهذه الدوائر الثمانية هي حل مسألة أبولونيوس.

تم تحديد ثماني دوائر متماسة لثلاثة دوائر معلومة (الملونة بالابيض). التي اثنتين منهما داخل الدائرة الثالثة كما هو مبين في الصورة المرفقة