مثلية التوضع

في علم الطوبولوجيا, إذا كان هناك دالتين مُتصلتين من فضاء طوبولوجي واحد لفضاء آخر فتُسمَّى مِثليَّة التوضُّع (اليونانية ὁμός (homós) = same, similar, and τόπος (tópos) = place) وإذا كانت إحدى الدالَّتين "معدَّلة التشكيل باستمرار" للأخرى، فمثل هذا التعديل يُسمَّى مِثليَّة التوضُّع بين هاتين الدالتَّين. من الاستخدامات البارزة لمفهوم مِثليَّة التوضُّع هو تحديد وتعريف زمر الهموتوبي (homotopy) وزمر الكوهموتوبي (cohomotopy), وهما من أهمَّ الثوابت الجبرية في الطوبولوجيا الجبرية.

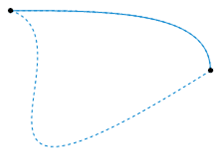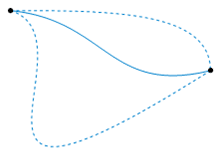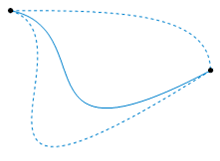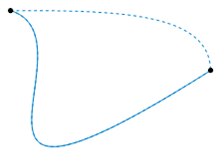
يفتقر محتوى هذه المقالة إلى الاستشهاد بمصادر. فضلاً، ساهم في تطوير هذه المقالة من خلال إضافة مصادر موثوقة. أي معلومات غير موثقة يمكن التشكيك بها وإزالتها. (ديسمبر 2018)
The two dashed paths shown above are homotopic relative to their endpoints. The animation represents one possible homotopy.

عمليًا، يوجد بعض الصعوبات التقنية في استخدام مِثليَّة التوضُّع مع فضاءات مُعيَّنة. يتعامل علماء الطوبولوجيا الجبرية مع الفضاء المُولِّد المُترَّاص، مركبات سي دباليو (CW complex), أو الأطياف.

التعريف الاصطلاحي
An isotopy of a coffee cup into a doughnut (طارة).

اصطلاحيًا، إذا ُوُجِدت مِثليَّة التوضُّع بين الدالتَّين المُتَّصلتين f وg من فضاء طوبولوجي X للفضاء الطوبولوجي Y إذًا فهذه دالَّة مُتَّصلة H : X × [0,1] → Y ناتجة من حاصل ضرب الفضاء X مع فترة المجموعة المُتكاملة [0,1] إلى Y حيث، إذا x ∈ X إذًا H(x,0) = f(x) وأيضًا H(x,1) = g(x).

وإذا اعتبرنا الوسيط الثاني للقيمة H على أنها تُمثِّل الوقت إذًا القيمة H توصف التعديل المُستمِّر للقيمة f في g: فعندما يكون الوقت 0 تكون الدالَّة f وحين يكون الوقت 1 تكون الدالَّة g.

إحدى الملاحظات البديلة هي أنه إذا وُجِدت مِثليَّة التوضُّع بين دالتَّين مُتَّصلتين f, g : X → Y هي مجموعة من الدالَّات المُتَّصلة ht : X → Y للقيمة t ∈ [0,1] حيث h0 = f وh1 = g, والرسم البياني t ↦ ht تصبح مُتَّصلة من [0,1] وحتى فضاء الدالَّات المُتَّصلة X → Y. وتتطابق الصيغتان من خلال تحديد ht(x) = H(x,t).

المراجع
  • Armstrong, M.A. (1979). Basic Topology. Springer. ISBN 0-387-90839-0. الوسيط |CitationClass= تم تجاهله (مساعدة)
  • Spanier, Edwin (1994). Algebraic Topology. Springer. ISBN 0-387-94426-5. الوسيط |CitationClass= تم تجاهله (مساعدة)

انظر أيضًا
  • زمرة ارتباط الصفوف
  • مِثليَّة التوضُّع
  • إتش بلاين لاوسن
  • مِثليَّة التوضُّع المُنتظمة
  • حدسية بوانكاريه
  • الطريقة التحلِّيليَّة لنظرية مِثليَّة التوضُّع


  • بوابة رياضيات
  • بوابة طوبولوجيا
مثلية التوضع في المشاريع الشقيقة
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.