متتالية بغوفر

في نظرية المخططات يُقرن رمز بغوفر (بالألمانية: Prüfer-Code) أو متتالية بغوفر إلى شجرة مسماة أحادياً (بانفراد). يبلغ طول شجرة مكونة من س رؤوس س-1 ، ويمكن توليده بخوارزمية بسيطة. تم استخدم هذه المتتالية لأول مرة في عام 1918م من قبل الألماني هاينز بروفر لإثبات صيغة كايلي.[1]

خوارزمية

تحويل شجرة لمتتابعة بغوفر

يُمكن تحويل شجرة بغوفر مسماة إلى متتابعة بإزالة الرؤوس بتتابع من الشجرة حتى يتبقى رأسان.على سبيل المثال، لتكن ش شجرة مسماة تحوي على {1،2،...س} رؤوس، في كل خطوة خ تُزال الأوراق ذات أصغر قيمة اسمية، وتحدد القيمة خ لمتتالية بغوفر بمسمى والدة الورقة. كل متتابعة لبغوفر تعتبر فريدة وطولها يصل لـ س-1.

مثال

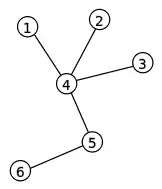
افرض أن الخوارزمية أعلاه طُبقت على الشجرة الظاهرة على الشكل أدناه، فالبداية الرأس بمسمى 1 سيكون ذو أقل قيمة، لذا ستتم إزالته، وتحديد قيمة 4 في متتالية بغوفر، بعدها بنفس العملية ستتم إزالة الرؤوس 2 و 3 ووضع 4 مرتين، أصبح الرأس 4 الآن ورقة بأصغر مسمى، لذا سيزال وتحدد القيمة 5 للمتتابعة. سيتبقى الآن رأسان، وهنا تتنهي الخوارزمية بنتيجة {4,4,4,5}.

شجرة مسماة بمتتالية بغوفر {4,4,4,5}.

مراجع
  1. Prüfer, H. (1918). "Neuer Beweis eines Satzes über Permutationen". Arch. Math. Phys. 27: 742–744. الوسيط |CitationClass= تم تجاهله (مساعدة)


    متتالية بغوفر في المشاريع الشقيقة
    • بوابة رياضيات
    • بوابة علم الحاسوب
    This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.