مبرهنة بيك

في الهندسة الرياضية، من أجل مضلع بسيط تم إنشاؤه على شبكة منتظمة من النقاط كما في الشكل المجاور بحيث أن جميع رؤوس المضلع هي نقاط من الشبكة، فإن مبرهنة بيك تعطي صيغة بسيطة لحساب مساحة المضلع A باستخدام عدد النقاط الداخلية i التي تقع داخل المضلع وعدد النقاط المحيطية b التي تقع على خط محيط المضلع بالعلاقة التالية:

${\displaystyle A=i+{\frac {b}{2}}-1.}$

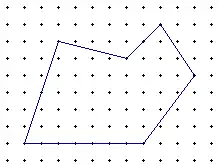
مضلع أنشأ على شبكة من النقاط المتساوية البعد عن بعضها البعض

في المثال الموضح بالشكل (i = 39) و(b = 14) وينتج أن مساحة الشكل هي A = 39 + 14/2 − 1 = 39 + 7 − 1 = 45 (وحدة مربعة).[1][2]

يمكن تطبيق هذه المبرهنة على المضلعات البسيطة فقط :تلك التي لا تتقاطع أضلاعها ولا تحوي أي مضلعات أخرى في داخلها.