قوة دفع المركبة الفضائية

قوة دفع المركبة الفضائية هي طريقة تستخدم لتسريع المركبات الفضائية والأقمار الاصطناعية هناك عدة طرق مختلفة وكل طريقة لها عيوبها ومزاياها، وقوة دفع المركبات الفضائية هي مجال بحث نشط تُدفع معظم المركبات الفضائية اليوم عن طريق قوة الغاز من الجزء الخلفي من المركبة بسرعة عالية جدا من خلال صوت فوهة لا فال ويسمى هذا النوع من المحركات بقوة دفع المركبة الفضائية بمحرك الصاروخ.

صورة مثبتة عن بعد تلتقط صور مقربة للحظات انتطلاق محركات دفع مكوك فضائي في مركز ستينيس للفضاء في مسيسيسبي.

تستعين معظم المركبات الفضائية الحالية بالصواريخ الكيميائية (الوقود الدافع الثنائي أو الوقود الصلب) في عملية الإطلاق وعلى الرغم من أن البعض (كصاروخ بيغاسوس سبيس شيب ون) قد استعان بمحركات دفع هوائية في المرحلة الأول. تستخدم معظم الأقمار الصناعية جهاز تضخيم كيميائي آمن وبسيط ( صواريخ الدفع الفردية في الغالب) أو صواريخ الريزيستوجيت للمحافظة على مدار المحطة وتوظيف بعض عجلات الدفع للتحكم في الآداء وقد استعانت مجموعة من الأقمار الصناعية السوفييتية بالدفع الكهربائي على مر العديد من العقود وبدأت أحدث المركبات الفضائية التي تسير في مدار الكرة الأرضية باستخدامها في المحافظة على المحطات الشمالية والجنوبية ورفع مستوى المدار وغالبا ما يتم الاستعانة بالصواريخ الكيميائية في مركبات الكواكب أيضًا على الرغم أن القليل يستخدم الدفع الأيوني والدفعات التي تحت تأثير هول (نوعين مختلفين من الدفع الكهربائي) و لاقت نجاحا كبيراً منها.

المتطلبات

معلومات إضافية: سرعة الإفلات

يجب إطلاق الأقمار الاصطناعية للمدار وفي حال وصولها يجب أن تأخذ مكانها في المدار الاسمي. للمرة الأولى في المدار المرغوب فهي تحتاج غالباً شكل من أشكال التحكم لذلك فهي تصحح الحدود المتعلقة بالأرض والشمس ومن بعض الفوائد المحتملة للأجسام الفلكية[1] فهي أيضا عرضة لجذب الأجسام الفلكية من الغلاف الجوي الرقيق لذا لكي تبقى في المدار لفترة زمنية طويلة فبعض أشكال الدفع قد تكون ضرورية من حين لأخر لإنجاز تصحيحات صغيرة في محطة المناورات المدارية[2] فالعديد من الأقمار الاصطناعية تحتاج للتحرك من مدار إلى آخر ومن حين إلى آخر وهذا أيضا يتطلب دفع حياة القمر الاصطناعي مفيدة بشكل كبير فهي تستنفذ قدرتها لتصحيح مدارها.[3] المركبة الفضائية مصممة للسفر المتواصل وهي في حاجة أيضاً لطرائق الدفع فهي بحاجة لمغادرة الغلاف الجوي للأرض كما هو الحال في الأقمار الاصطناعية وحال وصولها هناك فهي بحاجة لمغادرة المدار والتحرك حوله للسفر بين الكواكب. يجب على المركبة الفضائية استخدام محركاتها لمغادرة مدار الأرض وبمجرد حدوث ذلك يجب عليها ان تذهب بطريقة ما إلى وجهتها. فالمركبة الفضائية من بين الكواكب الحالية تفعل هذا مع سلسلة من التعديلات ذات المدى القصير.[4] ومن بين هذه التعديلات تسقط المركبة الفضائية ببساطة وبحرية على طول مسارها أكثر الوقود كفاءة تعني الانتقال من مدار دائري واحد إلى آخر مع نقل مدارهما وهو أنه تبدأ المركبة الفضائية في مدار دائري تقريبا حول الشمس فترة قصيرة من قوة الدفع في اتجاه الحركة تسرع أو تتباطأ في مركبة فضائية في مدار بيضاوي الشكل حول الشمس والتي تكون عرضية لمدارها السابق وأيضا إلى جهتها وتندرج المركبة الفضائية بحرية على طول هذا المدار البيضاوي الشكل حتى تصل إلى وجهتها وفترة أخرى قصيرة من التوجه حيث تسرع أو تتباطأ لتطابق المدار من جهتها[5] وهناك طرق خاصة مثل تخفيض السرعة بالكبح أو الإلتقاط الجوي تستخدم في بعض الأحيان لضبط المدار النهائي.[6]

رسم خيالي لفكرة "شراع الشمس".

بعض طرق دفع المركبات الفضائية مثل الأشرعة الشمسية توفر زخما منخفضا جدا ولكن لا ينضب.[7] إن استخدام المركبة لأحد هذه الأساليب سيجعلها تتبع مسارا آخر نوعا ما، إما ستدفع باستمرار ضد اتجاه الحركة من أجل تقليل المسافة التي تفصلها عن الشمس أو تدفع باستمرار في نفس اتجاه الحركة لزيادة المسافة التي تفصلها عن الشمس. هذا المفهوم اختبر بشكل ناجح من قبل اليابانيين IKAROS. الشراع الشمسي للمراكب الفضائية

تحتاج السفن الفضائية التي تُستخدَم في السفر بين النجوم أيضاً إلى أساليب معينة لإطلاقها ولم يتم حتى الآن بناء مثل هذه السفن ولكن تمت دراسة العديد من التصاميم وحيث أن المسافات بين النجوم هائلة فإننا نحتاج لسرعات عالية لإرسال سفينة فضائية باتجاه ما في فترة زمنية معقولة نسبياً ويعتبر الحصول على سرعات كهذه عند إطلاق تلك السفن وإنقاصها عند الهبوط تحدٍ كبير لمصممي السفن الفضائية.[8]

الفاعلية

في الفضاء، الهدف من نظام الدفع هو تغيير سرعة المركبة الفضائية. ولأن هذا يعد أكثر صعوبة على المركبات الفضائية الأكبر حجماً، قام المصممون بمناقشة زخم الحركة أو كمية الحركة، mv، بشكل عام. وتسمى كمية التغير في كمية الحركة بالدفع.[9] إذاً فالهدف من نظام الدفع في الفضاء هو تكوين الدفع.

عند إطلاق مركبة الفضاء من الأرض، يجب على نظام الدفع أن يتغلب على أعلى تأثير للجاذبية لينتج بذلك صافي التسارع الإيجابي.[10] في مسار الفلك، أي زيادة في الدفع، حتى لو كانت طفيفة، سينتج عنها تغير في ذلك المسار.

يطلق على معدل التغير في السرعة التسارع فيما يطلق على معدل التغير في الدفع القوة. وللوصول للسرعة المعطاة فيمكن للمرء تقديم تسارع صغير ينتهي بعد فتره زمنية طويله أو يمكنه تقديم تسارع كبير تنتهي بعد فتره زمنية قصيرة. وبنفس الطريقة يستطيع المرء تحقيق الدفع المعطى مع قوة كبيرة تنتهي بفترة قصيرة أو قوة صغيرة تنتهي بعد فترة طويلة. وينتج من هذا التسارع مناورة في الفضاء وطريقة الدفع التي تنتج تسارعات دقيقة ولكنها تستمر لفترة زمنية طويلة تستطيع إنتاج نفس الدقة كما في طريقة الدفع والتي تنتج تسارعات كبيره لمدة قصيرة فعندما يتم الإطلاق من الكوكب لا تستطيع التسارعات الدقيقة التغلب على قوة جاذبية الكوكب وبالتالي لا يمكن استخدمها.

سطح الأرض يقع عميقا إلى حد ما في بئر الجاذبية. سرعة الإنفلات التي تحتاجها للخروج منها هي 11.2كيلومتر في الثانية. ولقد، تطور البشر في مجال الجاذبية ذات الـ ون-جيي لكل متر واحد في الثانية تربيع، فإن نظام الدفع المثالي سيكون من النوع الذي يمنح تسارعاً مستمراً لـ ون-جيي (أن جسم الإنسان قادر على تحمل تسارعات أكبر في فترات قصيرة). الركاب في الصاروخ أو السفينة الفضائية، ذات نظام دفع مثل الذي ذكر، لن يضرهم أثار السقوط الحر، مثل الغثيان، ضعف العضلات، قلة في حاسة الطعم، أو تسرب الكالسيوم من عظامهم.

قانون المحافظة على الزخم يعني: تغيير زخم السفينة الفضائية باستخدام منهج الدفع، يجب أن تغير زخم شيء أخر في نفس الوقت.قليل من التصميمات تستخدم أشياء مثل النطاق الكهربائي أو ضغط الضوء لتغيير زخم السفينة الفضائية، ولكن في مساحة خالية يجب على الصاروخ أن يأتي ببعض الكتلة لتتسارع بعيدا من أجل دفع نفسه إلى الأمام. هذه الكتلة تسمى الكتلة التفاعلية.[10]

ليعمل الصاروخ يحتاج إلى شيئان، وهما بالترتيب: كتلة ردة الفعل والطاقة. يتأهب الدافع ويقوم بإطلاق جسيم من كتلة ردة الفعل m في سرعة v لتعطي mv. لكن هذه الجسيمات تتضمن الطاقة الناشطة أو الحركية mv²/2 والتي من المفترض أن تأتي من مكان ما. في حالة الصلب والسائل أو هجين الصاروخ، يتم حرق الوقود لتوفير الطاقة، ويُسمح لمنتجات التفاعل بالتدفق في الخلف لتوفير رد الفعل المتكتل. أما دافع الأيون فيستخدم الكهرباء لتسريع الأيونات من الخلف. هنا بعض المصادر الأخرى لتوفير الطاقة الكهربائية (لعل منها؛ الكسوف أو المفاعل النووي)، في حين أن الأيونات توفر كتلة رد الفعل[10]

عند مناقشة فعالية نظام قوة الدفع غالباً المصممين يركزون بفاعلية على ردة فعل الكتلة يجب أن يتم التفاعل الجماهيري جنبا إلى جنب مع الصواريخ ويستهلك عند استخدامها يجب القيام برّدة فعل الكتلة جنبا إلى جنب مع الصواريخ ويستهلك بشكل نهائي عند استخدامها وهناك طريقة واحدة لقياس كمية الاندفاع التي يمكن الحصول عليها من مقدار ثابت من ردة فعل الكتلة هوا الدافع محددة لكل وحدة وزن على الأرض (المعين عادة من قبل) وكل وحدة لهذه القيمة هي الثواني لأن الوزن على الأرض من ردة فعل الكتلة غالباً ما تكون غير هامة عند مناقشة المركبات في الفضاء ويمكن أيضا أن يتم مناقشة دفعة محددة من حيث الدافع لكل وحدة من الكتلة وهذا شكل بديل من دفعة محددة يستخدم نفس وحدات السرعة (على سبيل المثال م / ث) وفي واقع الأمر هو مساو لسرعة العادم الفعالة للمحرك (المسمى عادة) مشوش وتسمى في بعض الأحيان على حد سواء القيم دفعة محددة القيمتين تختلف بمعامل. G_nوتسارع المعيار بسبب الجاذبية 9.80665 م / ث² (I_spg_n=v).

الصاروخ ذو سرعة عادم عالية لديه القدرة على تحقيق نفس الدفعة بردة فعل أقل عموماً الطاقة اللازمة لهذا الدفع تتناسب مع سرعة العادم ولذا فإن المحركات ذات الكفاءة تحتاج لطاقة أكثر بكثير وتكون عادةً ذات كفاءة أقل في استخدام الطاقة وتكون هذه مشكله إذا كان المحرك يستخدم لمد مقدار كبير من الدفع. لتوليد المقدار الكبير من الدفع خلال ثانية يجب استخدام مقدار كبير من الطاقة خلال ثانية لذلك فإن المحركات ذات كفاءة الدفع العالية تحتاج مقدار ضخم من الطاقة قي الثانية لانتاج دفع عالي ونتيجة لذلك فإن معظم تلك المحركات تصمم لتزويد مقدار اقل من الدفع بسبب عدم توفر مقدار عالي من الطاقة.

الطرق

ويمكن تصنيف أساليب الدفع استنادا ًعلى وسائل تسريع كتلة رد الفعل هناك أيضا بعض الطرق الخاصة للإطلاق الوصول للكواكب والهبوط.

المحركات المرتدة الإرتكاسية

المحرك المرتد الارتكاسي هو محرك يُزود بالدفع عبر طرد الكتلة المرتدة وفقاً لقانون نيوتن الثالث للحركة وقانون الحركة هذا هو المقوله الأكثر شيوعاً لكل قوة فعل قوة فعل مرتدة مساوية لها في المقدار ومعاكسه لها في الاتجاه وتتضمن الأمثلة كلا من المحركات الأنبوبية ومحركات الصواريخ والكثير من الاختلافات النادرة مثل محرك إيون والناقل الدفعي للكتلة ومحركات تأثير هول المحركات الأنبوبية بالفعل تُستخدم لدفع في الفضاء نظراً لعدم وجود الهواء، غير أن بعض المركبات الفضائية لديها هذه الأنواع من المحركات لتساعدها في الهبوط والإقلاع.

دلتا الخامس والاندفاع الذاتي

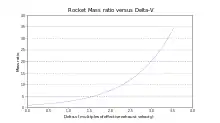
رسم يظهر علاقة نسب الكتلة مع السرعة النهائية كما يفهم من معادلة الصاروخ

قد ينتج إرهاق كامل الاندفاع صالح للاستعمال في مركبة فضائية من خلال المحركات في خط مستقيم في مساحة فارغة تغير السرعة الصافية للمركبة وأطلق على هذا العدد مصطلح دلتا الخامس ( $\Delta v$ ).

إذا كانت السرعة العادمة ثابتة فيمكن حساب كامل مجموع دلتا الخامس للمركبة ( $\Delta v$ ) باستخدام معادلة الصاروخ التي يكون فيها M هو كتلة الدافع و P كتلة الحمولة ( مشتملة تركيب الصاروخ ) و هو سرعة عادم الصاروخ وهي تعرف بمعادلة تشياكوفسكي الصاروخي: $\Delta v=v_{e}\ln \left({\frac {M+P}{P}}\right).$ ولأسباب تاريخية وكما نُوقش أعلاه V_e أحيانًا تكتب: $v_{e}=I_{sp}g_{o}$ حيث أن I_sp تعني النبضة/الدفعة المحددة لـ الصاروخ وتقاس بالثواني أما g_o فهي تسارع الجاذبية عند مستوى سطح البحر. ولـتكون مهمة دلتا الخامس عالية يجب أن تكون غالبية كتلة مركبة الفضاء من كتلة رد الفعل بما أن الصاروخ يجب أن يحمل جميع ردود فعل الكتلة غالبية رد فعل الكتلة المستهلك في البداية يخرج نحو رد فعل جماعي بدلًا من حمولة إذا كان لدى الصاروخ حمولة من الكتلة P، فـ مركبة الفضاح تحتاج طريق $\Delta v$ ، ومحرك الصاروخ يكون لديه سرعة العادم v_e، والكتلة M من رد فعلها والذي يتحاج إلى حساب استخدام معادلة وصيغة الصاروخ على النحو: : $M=P\left(e^{\Delta v/v_{e}}-1\right).$

و بالنسبة للمعادلة التي تقول بأن قيمة الدالة $\Delta v$ أصغر بكثير من قيمة الدالة V_e' هي تقريبا معادلة خطية، والشيء اليسير من كتلة التفاعل النووي تكون متطلبة. و بالتالي فإن قيمة الدالة $\Delta v$ - إذا كانت متساوية مع قيمة الدالة V_e' - في حاجة في أن يصبح لديها تقريبا ضعف كمية زيت الوقود الموجودة لدى الحمولة الإجمالية للمركبة الفضائية ولدى هيكلها مجتمعين مع بعضيهما ( و التي تتضمن المحركات، صهاريج الوقود، ونحو ذلك ). و بالإضافة إلى هذا، فإن النمو والازدياد "أسّي" (معبر عنه بالأس)، حيث أن معدلات السرعة أعلى بكثير من سرعة الحركة المستهلكة والتي تستوجب كميات هائلة من كتلة زيت الوقود حتى يتم تزويد السفينة الفضائية وما تحمله من أدوات ومواد، وتزويد كتلة المادة الهيكلية أيضا . و على سبيل المثال - بالنسبة للمهمة الفضائية - فإنه من اللازم أن تكون نتائج أو ظواهر الجاذبية الأرضية وأية آثار للسحب الجوي قد تأثرت بشكل كبير من جراء استخدام زيت الوقود عند وقت الانطلاق من الكوكب أو الهبوط إليه. و من المنطق يتم ربط هذه الآثار وربط الآثار الأخرى برحلة الفضاء الهامة للدالة $\Delta v$ . فمثلا : انطلاق البعثة الفضائية نحو مدار الأرض الأول يستوجب حوالي 9.3–10 km/s من قيمة الدالة $\Delta v$ . و رحلات الفضاء هذه للدالة $\Delta v$ قد تم إجراء عملية التكامل لها رقميا على جهاز حاسوب. و بالإمكان فقط أن يستفاد بشكل ملحوظ من بعض هذه التأثيرات (مثل تأثير أوبيرث) و ذلك عن طريق محركات قوة الضغط العالية مثل الصواريخ، بمعنى أن المحركات تستطيع أن تصدر قوة جاذبية دافعة (حيث أن قوة الضغط الهائلة لكل وحدة كتلة للمادة، متساوية مع قيمة الدالة $\Delta v$ لكل وحدة زمن).

استخدامات الطاقة والكفاءة الدفعية

بالنسبة لجميع محركات طاقة ردة الفعل (مثل الصواريخ والمشغلات الأيونية) يجب أن تخوض في عملية تسريع الكتلة التفاعلية، فيضيع قدرا من الطاقة عندها، وحتى لو افترضنا أن نسبة كفاءة المحرك تبلغ 100%، فجزء من الطاقة يذهب في تسريع تفريغ المحرك بما يصل إلى ${\frac {1}{2}}{\dot {m}}v_{e}^{2}$ [11]

ولا تعد هذه الطاقة مهدرة حيث أن جزءا منها يكون طاقة حركية للمركبات، كما يضيع قدرا منها في حركة التفريغ المتبقية.

هذه الطاقة ليست بالضرورة مهدرة غالباً يتحول بعضها كطاقة حركية للمركبة والباقي يُهدر في الحركة المتبقية للعادم.

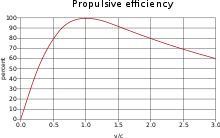
تتغير نسبة كفاءة محرك ردة الفعل مع سرعة العادم وسرعة المركبة وذلك لأن طاقة تنتقل عبر العادم. وهذا ما يسمى بطاقة الدفع.

عند مقارنة كلاً من معادلة الصاروخ ( التي تُظهر مقدار الطاقة التي تصل إلى الآلة الأخيرة) والمعادلة السابقة ( التي تُظهر إجمالي الطاقة اللازمة ) فإنه حتى إن بلغت كفاءة المركبة 100% حتماً لن تصل كل الطاقة المزودة إلى المركبة البعض منها بل غالباً معظمها يؤول بها المطاف لتصبح طاقة حركية للعادم.المقدار الفعلي يعتمد على تصميم المركبة، وطبيعة المهمة إلا أنه توجد بعض العوامل الثابتة المفيدة كالتالي:

في حال ثبات الدفع النوعي $I_{s}p$ ، لمعامل تغير السرعة فإنه يوجد مقدار معيّن للدفع النوعي $I_{s}p$ لتقليل الطاقة الإجمالية التي يستغلها الصاروخ، هذا يؤدي لبلوغ سرعة العادم مقدار $2/3$ معامل تغير السرعة ( راجع الطاقة المقَدرة من معادلة الصاروخ) فالمحركات التي لها دفع نوعي عالي وثابت مثل المحركات الأيونية تتميّز بسرعة عادم تفوق بكثير السرعة النموذجية للعديد من المهام
إذا أمكن جعل سرعة العادم متغيرة بحيث تكون في كل لحظة مساوية ومقابلة لسرعة المركبة بالتالي يمكن تحقيق الحد الأدنى لإستغلال الطاقة عند تحقيق ذلك، أي عندما يتوقف العادم في الفضاء ولا توجد طاقة حركية؛ وتبلغ الكفاية الدفعية 100% عندها ستصل الطاقة بأكملها إلى المركبة ( نظرياً ستبلغ كفاءة المحرك 100% لكن عملياً ستوجد خسارة حرارية داخل نظام المحرك وهي حرارة ناتجة من العادم ). إلا أنه في أغلب الحالات يتم استخدام مقدار دفع غير عملي لكنها فكرة نظرية فعالة على أي حال يجب إطلاق المركبة قبل إمكانية تطبيق هذه الطريقة.

تتفاوت بعض المحركات في سرعة العادم فيها (مثل محرك فاسيمر أو دافع البلازما خالي الاقطاب) مما قد يساهم في تقليل استخدام الاندفاع الذاتي أوتحسين التسارع في مراحل مختلفة اثناء الرحلة وأفضل اداء حيوي ممكن يحصل فقط حين تتقارب سرعة العادم وسرعة المركبة وتحتوي محركات البلازما والمحركات الأيونية الحالية عادة على عوادم ذات سرعات هائلة أعلى من المحركات النموذجية (و كمثال كانت ادنى سرعة لمحرك فاسيمر تم تسجيلها تقارب 1500م/ث مقارنة بمحرك ديلتا في من مدار أرضي مرتفع للمريخ والتي كانت تقارب 4000م/ث)

قد يعتقد البعض أن زيادة الطاقة لقدرة التوليد قد يكون مفيداً في حين انه مبدئياً قد يحسن هذا من فعالية الأداء الا انه حتماً سيزيد من وزن مصدر الطاقة وبالنهاية فان كتلة كل من مصدر الطاقة والمحرك وما يحويه من وقود وغازات متفاعلة يتشاركون جميعاً في التحكم بوزن المركبة حينها فان زيادة الطاقة لا يكون له أي فائدة ملحوظة.

إلا أن كل من الطاقة الشمسية و الطاقة النووية هما تقريباً مصدران غير محدودين من الطاقة الحد الأقصى الذي يمكنهما توفيره غالباً متناسب مع حجم المحرك ومولد الطاقة (مثال: قوة محددة تاخذ قدر كبير من قيمة مستمرة الذي تعتمد بدورها على تقنية "محطة توليد الطاقة" المعينة) لأي قوة محددة معطاة مع سرعة كبيرة والتي يرجى منها حفظ حجم الوقود والغازات المتفاعلة في المحرك حينها يظهر لنا أن الحد الأقصى للتسارع متناسب عكسياً مع السرعة لذا فالزمن للوصول إلى دلتا السرعة المطلوبة متناسب مع السرعة v_e وهكذا أخيراً لا يجدر به أن يكون كبيراً جداً. لذا فالزمن للوصول إلى دلتا السرعة المطلوبة متناسب مع السرعة، وهكذا أخيراً لا يجدر به أن يكون كبيراً جداً.

الطاقة

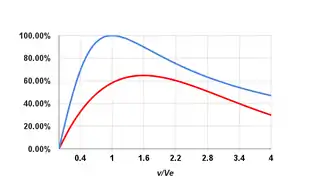
رسم تخطيطي لكفاءة دفع أنية (اللون الأزرق) والكفاءة الكلية لمركبة تتسارع من الوقوف (اللون الأحمر) كنسبة مئوية من كفاءة المحرك.

في الحالة المثالية فإن m₁ ترمز للحمولة و m₀-m₁ هي مقدار الكتلة المعاكسة (وينطبق هذا على الصهاريج الفارغة التي لا كتلة لها، وما إلى ذلك) وتستخدم المعادلة التالية لحساب الطاقة اللازمة]]

${\frac {1}{2}}(m_{0}-m_{1})v_{\text{e}}^{2}$ .

ويمكن استخدامها أيضًا لحساب الطاقة الحركية الناتجة من الكتلة المعاكسة حين تكون بسرعة تساوي سرعة العادم؛ ولتسريع الكتلة المعاكسة من السكون وحتى سرعة تعادل سرعة العادم فإن الكتلة المعاكسة ستستهلك كل الطاقة الناتجة دون أن يبقى منها شيء للطاقة الحركية المكتسبة في كلا من القذيفة والحمولة. ولكن في حال تحرُك القذيفة وتسارعها فإن الكتلة المعاكسة ستطرد بالإتجاه المعاكس لإتجاه حركة القذيفة؛ مما يضيف طاقة حركية أقل للكتلة المعاكسة. فعلى سبيل المثال - حتى نفهم هذا - إذا كانت الدالة v_e= 10 كم / ثانية وسرعة الصاروخ على بعد 3 كم / ث، ثم سرعة كمية صغيرة من الكتلة الممتدة تتغير من 3 كم / ث إلى الأمام إلى 7 كم / ث نحو الخلف وبالتالي فإن مقدار عشرين جول من جهد الطاقة فقط يستخدم من أجل الزيادة في سرعة كتلة التغير بينما المقدار المطلوب هو خمسين جول من جهد الطاقة لكل كيلو جرام واحد من كتلة التفاعل النووي ومقدار الثلاثين جول المتبقي من جهد الطاقة هو ازدياد الطاقة الحركية للصاروخ وللحمولة الإجمالية الخاصة به. وبشكل عام فإن

$d\left({\frac {1}{2}}v^{2}\right)=vdv=vv_{\text{e}}dm/m={\frac {1}{2}}\left(v_{\text{e}}^{2}-(v-v_{\text{e}})^{2}+v^{2}\right)dm/m$

و لذلك فإن ارتفاع معدل الطاقة النوعية للمحرك الصاروخي في أي فترة زمنية قصيرة هو الاكتساب في طاقة الصاروخ متضمنا زيت الوقود المتبقي مقسما على كتلته حيث أن مقدار ازدياد الطاقة هو مساوي للطاقة المنتجة عن طريق زيت الوقود منقوصا منه الطاقة المكتسبة لكتلة التغير وكلما كانت سرعة الصاروخ أكبر وكلما كانت الطاقة المكتسبة لكتلة التفاعل النووي أصغر إذا كان مقدار سرعة المحرك الصاروخي أكثر من نصف مقدار السرعة المتسربة من كتلة التغير حتى لو فقدت قوتها في حال أن تم إقصائها وذلك تعويضا للطاقة المكتسبة للصاروخ وكلما كانت سرعة الصاروخ أكبر وكلما كان فقدان الطاقة لكتلة التفاعل النووي أكبر.

لدينا $\Delta \epsilon =\int v\,d(\Delta v)$ حيثُ تعني الطاقة المحددة للصاروخ ( الطاقة الكامنة والحركية ) $\Delta v$ و تعني المتغير المستقل وليس فقط المتغير في (v).في حالة استخدام الصواريخ لعملية التباطؤ. أي في طرد كتلة رد الفعل في اتجاه السرعة، عندها يجب أن تكون (v) عكسية.

ومرة أخرى وضعت هذه المعادلة للحالات المثالية وعندما لا تُفقد الطاقة بفعل الحرارة إلخ... والتي تسبب إنخفاض في مستوى الدفع لذلك تُعتبر عائق حتى وإن كان الهدف هو فقدان الطاقة ( التباطؤ).

وإذا أنتجت الكُتلة ذاتها هذه الطاقة، مثلما يحدث في الصواريخ الكيميائية، فإن قيمة الوقود تكون ( $\scriptstyle {v_{\text{e}}^{2}/2}$ ) ويجب أن يؤخذ بعين الإعتبار أيضاً كتلة المؤكسد كقيمة الوقود تماماً.

القيمة النموذجية v_e= 4.5 km/s متناظرة مع قيمة الوقود 10.1 MJ/kg ويفترض أن تكون القيمة الفعلية للوقود أعلى من ذلك، لكن معظم الطاقة تُفقد كحرارة ضائعة في العادم التي لم تتمكن فوهته من إخراجها.

الطاقة المطلوبة E هي:

$E={\frac {1}{2}}m_{1}\left(e^{\Delta v\ /v_{\text{e}}}-1\right)v_{\text{e}}^{2}$

نستنتج أن

لكل $\Delta v\ll v_{e}$ لدينا $E\approx {\frac {1}{2}}m_{1}v_{\text{e}}\Delta v$
وللمعطية $\Delta v$ سيُحتاج الحد الأدنى من الطاقة إذا $v_{\text{e}}=0.6275\Delta v$ تتطلّب طاقة $E=0.772m_{1}(\Delta v)^{2}$ وفي حالة التباطؤ في اتجاه ثابت والبداية من سرعة الصفر وغياب أنواع القوى الأخرى سيعد هذا أفضل بنسبة 54.4% من مجرد الطاقة الحركية النهائية للحمولة الصافية وفي هذه الحالة المُثلى تكون الكتلة الأولية 4.92 مرّة من الكتلة النهائية تنطبق هذه النتائج كذلك على سرعة العادم الثابتة.

نظرًا لتأثير أوبرث وبدءًا من السرعة الصفرية فقد تكون الطاقة الكامنة اللازمة والمطلوبة من الوقود أقل من الزيادة في الطاقة في المركبة أو الحمولة قد تكون هذه هي الحالة عندما تقل سرعة رد الفعل الشامل بعد أن يطرد أكثر من قبل فالصواريخ لها القدرة على تحرير بعض أو كل الطاقة الحركية الأولية للوقود ولهدف معين أيضًا كالانتقال من مدار إلى آخر فقد يعتمد دلتا الخامس اللازم إلى حد كبير على المعدل الذي يستطيع المحرك إنتاج دلتا الخامس منه بل قد تكون المناورات مستحيلة إذا كان ذلك المعدل منخفضًا فمثلًا إطلاق ليو يتطلب عادة دلتا الخامس 9.5 كلم (تقريبًا حتى تكتسب السرعة) لكن إذا استطاع المحرك إنتاج دلتا الخامس بمعدل أكثر قليلًا فقط منقوة التسارع أو قوة جي فإنه سيكون إطلاقًا بطيئًا يستلزم دلتا الخامس كبير كليًا) تفكر في التحليق بدون إحراز أي تقدم في السرعة أو الارتفاع فإنه قد يكلف دلتا الخامس 9.8 أمتار في كل ثانية) إذا كان المعدل المحتمل قوة جي أو أقل فلا يمكن أن يتم المناورة بها إطلاقًا مع هذا المحرك.

تحسب القدرة بالقانون التالي: $P={\frac {1}{2}}mav_{\text{e}}={\frac {1}{2}}Fv_{\text{e}}$

حيث (F) هي القوة و( m) هي الكتلة بينما a هي التسارع بالنسبة للقوة وهكذا فإن القوة لكل وحدة قدرة تُقسم على 2 للدفعة المعطاة في المتر لكل ثانية وهكذا فإن الكفائة ( efficiency) للقوة (F) هي القوة الفعلية كنسبة مئوية لها.

على سبيل المثال في حال استخدام القدرة الشمسية فإن ذلك يحُد من قيمة التسارع (a)؛أي عندما تكون السرعة (Ve) عالية فإن التسارع يتناسب عكسياً مع السرعة (Ve)، كما أن الوقت (t) اللازم للوصول لفرق السرعة ( v∆ ) يتناسب طردياً مع ( Ve) بكفائة (efficiency) تساوي 100٪.

بما أن $\Delta v\ll v_{\text{e}}$ فإن $t\approx {\frac {mv_{\text{e}}\Delta v}{2P}}$

أمثلة:

إذا كانت القدرة = 1000 واط(W) والكتلة (m) تساوي 100 كيلو غرام(Kg) وفرق السرعة v∆ تساوي 5 كيلو متر لكل ثانية (Km/s) والسرعة V_e تساوي 16 كيلو متر لكل ثانية (Km/s) فإن الوقت (t)= شهر ونصف.
إذا كانت القدرة = 1000 واط(W) والكتلة (m) تساوي 1000 كيلو غرام(Kg) وفرق السرعة v∆ تساوي 5 كيلو متر لكل ثانية (Km/s) والسرعة Ve تساوي 50 كيلو متر لكل ثانية (Km/s) فإن الوقت (t)= خمسة أشهر.

نسبة االقوة إلى الدفع

نسبة القوة إلى الدفع هي ببساطة:[11] ${\frac {P}{F}}={\frac {{\frac {1}{2}}{{\dot {m}}v^{2}}}{{\dot {m}}v}}={\frac {1}{2}}v$

ولذلك فإن الدفع الذي يمكن تقديمه لأي طاقة مركبة P هو:

$F={\frac {P}{{\frac {1}{2}}v}}={\frac {2P}{v}}$

مثال

لنفترض أنّا نريد إرسال مجس فضائي يزن 10,000 كجم إلى المريخ فإن دلتا الخامس الضروري لإطلاق ليو يساوي تقريبًا 3000 م/ث باستخدام مدار هوهمان الانتقالي ومن أجل الجدال لنقل أن الدافعات التالية قد تستخدم وقوداً كتلته أقل بكثير.

المحرك	سرعة العادم الفعالة (كم/ث)	الدفعة المحددة (ث)	كتلة الوقود (كغ)	الطاقة المطلوبة (GJ)	طاقة لكل كيلو دفع	أقل قيمة طاقة/دفع (كيلو وات/نيوتن)	توليد قوة كتلة/دفع*
وقود صلب	1	100	190,000	95	500 kJ	0.5 kW/N	-
صاروخ ذو دفع ثنائي	5	500	8,200	103	12.6 MJ	2.5 kW/N	-
دافع أيوني	50	5,000	620	775	1.25 GJ	25 kW/N	25 kg/N

لُوحظ أن المحركات الأكثر كفاءة في استخدام الوقود يمكن أن تستخدم وقودًا أقل بكثير؛ كتلته تقريبًا مهملة -بالنسبة لكتلة الحمولة والمحرك نفسه- لبعض المحركات. على أية حال، لُوحظ أيضا أن هذا يتطلب كمية كلية كبيرة من الطاقة للإطلاق من الأرض، تحتاج هذه المحركات إلى نسبة دفع-وزن أعلى من واحد لعمل هذا بواسطة المحرك الأيوني أو عدد من محركات الأقراص الكهربائية النظرية، قد يحتاج المحرك إلى أن يُزود بطاقة تعادل 1 جيجاواط أو أكثر والذي يعادل محطة توليد لمدينة رئيسية كبيرة.

من خلال الجدول، يمكن بوضوح معرفة أن هذا غير عملي مع مصادر الطاقة الحالية، لكن ثمة مقاربات بديلة تتضمن بعض أشكال الدفع بالليزر، حيث أن كتلة رد الفعل لا توفر الطاقة المطلوبة لتسارعها، مع كون الطاقة موفرة بواسطة ليزر خارجي أو نظام طاقة مبثوثة آخر، بدلًا عن ذلك تم تشغيل بعض النماذج المصغرة لبعض هذه الفرضيات، برغم تعقيد المشاكل الهندسية وعدم حل مشكلة أنظمة مصادر الطاقة الأرضية.

في المقابل يمكن تضمين مولد أقل قوة والذي سوف يستغرق وقتًا أطول بكثير لتوليد الطاقة الكلية اللازمة، وهذه القدرة المحدودة تكفي فقط لتسريع كمية ضئيلة من الوقود في الثانية والتي لن تكون كافية للإنطلاق من الأرض. ومع ذلك وعلى مدى فترات طويلة في المدار حيث لا يوجد احتكاك سوف تتحقق السرعة، فعلى سبيل المثال SMART-1 استغرقت أكثر من سنة للوصول إلى القمر بينما الصاروخ الكيميائي يستغرق بضعة أيام؛ وذلك لأن المحرك الأيوني يحتاج إلى وقود أقل بكثير من غيره، بالتالي إجمالي الكتلة التي أُطلقت عادةً ما تكون أقل، والتي تُنتَج عادةً بتكلفة إجمالية أقل ولكنها تستغرق وقتاً أطول.

ولذلك فإن التخطيط للمهمّة كثيراً ما يشمل على اختيار وضبط نظام الدفع للتقليل من التكلفة الإجمالية للمشروع وكذلك يشمل على تداول لتكاليف الإطلاق ومدة المهمة ضد حمولة الكسر.

محركات الصواريخ

امتحان تشغيل محرك كيسترل لمركبة سبايس أكس

تعمل معظم محركات الصواريخ عن طريق الاحتراق الداخلي لحرارة المحركات( أيضاً أشكال الإخراج الغير محترقه) وبشكل عام محركات الصواريخ تصدر درجة حرارة عالية نتيجة ردة فعل الضغط مثال عليه الغاز الساخن وينتج ذلك بواسطة احتراق الوقود الصلب والوقود السائل والوقود الغازي مع الأوكسيدر في دائرة الإحتراق وأقصى حد للغاز الساخن هو أن يسمح له بمرور الغاز من خلال فوهة متوسط التمدد العالية فهذا الشكل المعدني للفوهة هو ما يعطي محرك الصاروخ هذا الشكل الخاص يعد التأثير على الفوهة بشكل هائل بسبب تسارع الضغط.وتحول معظم الطاقة الحرارية إلى طاقة حركية واستنفاذ سرعة وصول عاليه أعلى 10 مرات من سرعة الصوت في مستوى البحر كما هو شائع.]]

الصاروخ آلة مزودة جوهريًا بأعلى القوى النوعية ودافعة نوعية أعلى من أي آلة تُستخدم لتسيير السفن والمركبات الفضائية، دفع الصواريخ الأيوني يستطيع تسخين بلازما الدم أو يحمّل بالغاز داخل قنينة مغناطيسية ويُحرر عبر منفث مغناطيسي بحيث لا تحتاج إلى مسألة قاسية للدخول في ربط مع البلازما بالطبع الآلات التي تقوم بذلك معقدة لكن الأبحاث في الالتحام النووي لديها أساليب مطورة بعضها كان مقترحًا للاستخدام في نظام الدفع وبعضها جُرّب في المختبر، شاهد آلة الصاروخ لإثبات أنواع متعددة من الصواريخ التي تستخدم طرق تسخين مختلفة تشمل الكيميائي الكهربائي الشمسي والنووي.

الدفع الكهرومغناطيسي

محرك اختباري يعمل بتسارع الأيونات مستخدما قوة إلكتروستاتيكية

عوضاً عن الإعتماد على درجة الحرارة العالية وديناميكية السوائل لتسريع كتلة رد الفعل إلى سرعات عالية، هنالك طرق مختلفة تُستخدم فيها القوة الكهربائية أو الكهرومغناطيسية لتسريع هذه الكتلة بشكل مباشر وعادة ما تكون هذه الكتلة عبارة عن تيار من الأيونات فمثلا تستخدم الآلات الطاقة الكهربائية لتأيين الذرات أولا ومن ثم إنشاء تدرج في الجهد لتسريع الأيونات فتصل إلى سرعات عالية الجهد، تعود فكرة الدفع الكهربائي إلى عام 1906م عندما دوّن روبوت قودارد الإحتمالية في مفكرته الشخصية ونشرها كونستانتين تشياكوڤيسكي في عام 1911م.

أعلى سرعات العادم لهذه المحركات ذات جهد فعال وموجه عكسيا بالتناسب مع سرعة العادم فسرعة العادم العالية جدا يعني أنها تتطلب كميات هائلة من الطاقة وبالتالي فإن مصادر الطاقة الكامنة توفر توجه منخفض ولكن بصعوبه يستخدم أي نوع من الوقود بالنسبة لبعض البعثات، لا سيما القريبة إلى الشمس قد تكون الطاقة الشمسية كافية وكثيرا ما تم استخدامها ولكن للبعثات الأخرى خارجية أو طاقتها عالية تعد الطاقة النووية ضرورية فتستمد المحركات طاقتها من مصدر نووي يسمى الصواريخ الكهربائية النووية.

ان أكبر قدر من الطاقة التي يمكن توليدها مع أية مصادر للطاقة الكهربائية أو الكيميائية أو النووية أو الشمسية يحد من كمية الدفع التي يمكن أن تنتجها إلى كميات أصغر ويضيف توليد طاقة كتلة كبيرة إلى المركبة الفضائية وبالتالي يحد من وزن مصدر الطاقة في نهاية المطاف من آداء المركبة. وتشكل مولدات الطاقة النووية الحالية ما يقارب من نصف وزن الألواح الشمسية لكل واط من الطاقة الموردة على مسافات أرضية من الشمس ولا يتم استخدام مولدات الطاقة الكيميائية بسبب كمية الطاقة المتاحة القليلة جداً وتنم الطاقة الإشعاعية عن بعض الإحتمالات للمركبة الفضائية.

بعض الأساليب الكهرومغناطيسية:

أجهزة الدفع الأيوني (تسريع الأيونات الأولى في وقت لاحق وتحيد شعاع أيون مع تيار الإلكترونات المنبعثة من الكاثود يسمى التعادل).
- الأيون الكهربائي.
- مجال انبعاثات الدفع الكهربائي.
- تأثير قاعة الدافع.
- الدافع الغروانية.
أجهز الدفع الكهروحرارية ( تستخدم المجالات المغناطيسية لتوليد البلازما وبالتالي رفع الحرارة في كمية الوقود الدفعي تُنقل الطاقة الحرارية بعد ذلك للغاز الدفعي ومن ثم تحول إلى طاقة حرارية عن طريق الفوهة في بنية الأدوات الفيزيائية أو الوسائل المغناطيسية)
- أجهز دفع الأركجت.
- أجهزة دفع المايكرويڤ.
- دافع نابض البلازما.
أجهزة دفع الصاروخ الإزدواجية.
أجهز الدفع الكهرومغناطيسية ( تتسارع الأيونات إما عن طريق قوة لورنتز أو عن طريق تأثير الحقل الكهرومغناطيسي حيث الحقل الكهربائي ليس في إتجاه التسارع).
- دافع البلازما الممغنطة الدينامكية.
- دافع ايلكتروديس بلازما.
- دافع الإستقرائي النابض (متغير دفع محدد لصواريخ البلازما المغناطيسية. VASIMR)
مشغلات الكتلة للدفع

في أجهزة الدفع الكهروحرارية والكهرومغناطيسية تتسارع كل من الأيونات والإلكترونات في وقت واحد ولا يلزم التعادل.

ردة الفعل بدون كتلة داخلية

دراسات وكالة ناسا للشراع الشمسي. يصل عرض الشراع إلى نصف كيلومتر.

نظام بقاء كمية الحركة غالبًا ما يستخدم ليدل على أن أي مركبة لا تستخدم تفاعل الكتلة لا تستطيع تسريع مركز كتلة سفينة الفضاء ( تغيير الاتجاه - من ناحية أخرى - ممكن ) لكن الفضاء ليس بفارغ لاسيما الفضاء داخل المنظومة الشمسية ثمة مجالات جاذبية مجالات مغناطيسية، موجات كهرومغناطيسية، المجموعة الشمسية والإشعاع الشمسي.]]

الموجات الكهرومغناطيسية بذاتها تعرف باستيعابها القوة الدافعة بالرغم من كونها عديمة الكتلة لا سيما تدفق القوة الدافعة الكثيفة P للموجات الكهرومغناطيسية بكمية 1/c مضروبًا في متجه بوينتينغ S، أي بمعنى P = S/c عندما C تعني سرعة الضوء بمعنى أنها طرق تسيير المجال فهي تعتمد على تفاعل الكتلة وبالتالي يجب التجربة لإيجاد فائدة من هذه الحقيقة عن طريق دمج مجال أثر الحركة مثل الموجات الكهرومغناطيسية التي تتواجد بالقرب من المركبة ومع ذلك العديد من هذه الظواهر منتشرة في الطبيعة هيكل الدفع المتوازي بحاجة لأن يصبح أكبر بشكل متناسب.

يوجد العديد من المحركات الفضائية التي لا تحتاج إلى كتلة رد الفعل أو قد تحتاج إلى القليل منها فقط للقيام بعملها ومنها نظام الدفع بالكابلات الفضائية وهو كابل طويل ذو قوة شد عالية يستخدم لتغيير مدار المركبة الفضائية كأن يتفاعل مع المجال المغناطيسي للكوكب أو يتبادل الزخم مع الأجسام الأخرى وأيضاً الأشرعة الشمسية والتي تعتمد على الضغط الإشعاعي الصادر عن الطاقة الكهرومغاطيسية ولكنها تتطلب مجموعة سطحية كبيرة لتعمل بفاعلية الشراع المغناطيسي بقوم بتحويل الأجسام المشحونة بالرياح الشمسية عن مسارها بالمجال المغناطيسي وبالتالي يمد المركبة الفضائية بالزخم المناسب. والمتغير هو نظام الدفع ببلازما الغلاف المغناطيسي المصغّر، والذي يستخدم السحابة الصغيرة البلازمية الموجودة في المجال المغناطيسي لتحويل جزيئات الشمس المشحونة عن مسارها وأما شراع E أو الشراع الإلكتروني فيستخدم أسلاك رقيقة ممتلئة بشحنة كهربائية لتحويل تلك الجزيئات المشحونة عن مسارها وبطريقة قد تكون أكثر تحكماً لإتجاهها.

والمتغير هو نظام الدفع ببلازما الغلاف المغناطيسي المصغّر، والذي يستخدم السحابة الصغيرة البلازمية الموجودة في المجال المغناطيسي لتحويل جزيئات الشمس المشحونة عن مسارها. وأما شراع E أو الشراع الإلكتروني فيستخدم أسلاك رقيقة ممتلئة بشحنة كهربائية لتحويل تلك الجزيئات المشحونة عن مسارها وبطريقة قد تكون أكثر تحكماً لإتجاهها..

و قد أصبح قمر النانو - دي - القمر الصناعي الأول ليدور حول الأرض، كإثبات لهذا المفهوم العام [14] و هناك خطط لإضافتهم [يتطلب التوضيح] إلى مدار أقمار الأرض الصناعية المستقبلية، وتمكينها من عدم الدوران حول الأرض وإحراقها مرة واحدة بحيث لا يعد لها حاجة بعد ذلك. و يسعى مركب الشراع الفضائي والمكعب الشكل إلى معالجة أنقاض الفضاء.[15]

و إضافة إلى هذا، فقد أطلقت اليابان سفينتها الفضائية والمزودة بطاقة مركبة الشراع الشمسية العالية ( آيكاروس ) في شهر مايو من سنة 2010 ميلادية. و أوضحت ( آيكاروس ) علميا قوة السرعة والتوجيه بشكل ناجح، ولا تزال تسبح في الفضاء إلى هذا اليوم.

إن القمر الصناعي أو حتى أية مركبة فضائية أخرى يخضعون لقانون بقاء كمية التحرك الزاوي والذي يرغم ويجبر الجزء الرئيسي على التغير الجذري أو التحول التام من خلال قانون السرعة الزاوية وبالتالي فإنه من المحتمل أن يدور جزءا آخر من المركبة في الاتجاه المعاكس حتى تغير موقعها النسبي من غير أن تستنفد كتلة المفاعل النووي وتستطيع القوى الخارجية غير المحافظة ( و تأتي في مقدمتها القوى الجاذبية والقوى الجوية ) أن تسهم في الوصول إلى درجات متنوعة في اليوم الواحد من خلال قانون كمية التحرك الزاوي[12] ولهذا فإن الأنظمة الثانوية قد صممت للتخلص من مصادر الطاقة الدوارة والضارة والتي تستفحل وتتضخم تدريجيا عبر الزمن وهناك سفن فضائية عديدة تستخدم جهاز جيرسكوب لضبط كمية التحرك وجهاز دولاب تنظيمها من أجل أن تتحكم بالموقع في الفضاء.[13] مقلاع الجاذبية يمكن أن يحمل مسبار فضائي صاعدا إلى وجهات أخرى وذلك دون الحاجة لحساب كتلة ردة الفعل يتم ذلك عن طريق تسخير طاقة الجاذبية من الأجسام السماوية الأخرى، حيث يمكن لمركبة الفضاء التقاط الطاقة الحركية[14] ومع ذلك المزيد من الطاقة يمكن الحصول عليها من مُساعد الجاذبية إذا تم استخدام الصواريخ حيث أن كمية دافع البلازما الكهربائية هو الدافع النظري الذي يستخدم كمية التقلّبات الكهربائية لدفع مركبة فضائية.

دفع الكواكب والغلاف الجوي

آليات الإطلاق

تجربة ناجع لفكرة المركبة الخفيفة، نوع من أنواع الدفع باشعة ٫ات طاقة.

الدفع العالي أمر ذا أهمية لإطلاق الأرض ويجب أن تكون قوة الدفع أقوى من الوزن ( انظر أيضا إلى سحب الجاذبية )وتعطي العديد من طرق الدفع المذكورة اعلاه نسبة الدفع / الوزن أقل بكثير من 1 إذ لا يستطيع استخدامها. وتستخدم جميع المركبات الفضائية محركات صورايخ كيميائية ( الإندفاع الثنائي أو العمل بالوقود الصلب) للدفع فمصادر الطاقة الاخرى كالنووي المقترحة والمختبرة على أنها أمانه قد تقلت اعتباراتها السياسية والبيئية لاستخدامها حتى الآن.

الميزة الواحدة في اطلاق المركبة الفضائية هي توفر البنية التحتية في الأرض لمساعدتها تشمل آليات الإطلاق الفضائي المفترض لغير الصواريخ المبني على الأرض:

مصعد الفضاء ( حبل ثابت بالنسبة للأرض إلى المدار ).
حلقة الإطلاق ( حلقة مغلقة دورية سريعة جدا بطول 80 كم ).
نافورة الفضاء (مبنى طويل جدا عقد بتيار من الكتل أطلقت من القاعدة ).
الحلقة المدارية (حلقة حول الأرض مع مكابح تتدلى خارج المحامل ).
خطاف سمائي بسرعة مفرطة ( حبل مداري يدور بسرعة ).
منجنيق كهرومغناطيسي ( بندقية كهربائية).
مزلقة إطلاق صواريخ.
بندقية الفضاء ( مشروع HARP مسرع رام ) (بندقية تعمل بالطاقة الكيميائية ).
صواريخ دفع تعمل بالطاقة الإشعاعية وطائرات تعمل بالطاقة من الأرض عن طريق الإشعاع.
منصات عالية الإرتفاع لمساعدة المرحلة الأولى.
المنطاد المداري.

المحركات التي تتنفس الهواء

مقالة مفصلة: محرك نفاث

أظهرت الدراسات عموماً أن المحركات المألوفة التي تتنفس الهواء مثل المحرك النفاث بالوقود (رامجيت) أو المحرك النفاث العنفي (توربوجيت) تكون ثقيلة جداً (لديها نسبة دفع على وزن منخفضة جداً) بحيث أنها لن تعطي أي تحسن ملحوظ في الأداء حين يتم تركيبها على مركبة الإطلاق. مع ذلك، يمكن أن تطلق مراكب الإطلاق من الهواء من مراكب حمل منفصلة (مثلاً: بي-29، صاروخ بيغاسوس ووايت نايت) تستعمل هذه المنظومة في الدفع من الممكن أيضاً استعمال محركات نفاثة مركبة على سكة إطلاق.

من ناحية أخرى تم اقتراح محركات خفيفة الوزن أو سريعة جداً لاستغلال الهواء خلال الصعود،

سابري: محرك توربو نفاث خفيف الوزن مزود بوقود من الهايدروجين مع مبرد مسبقاً[15]
أتريكس: محرك توربو نفاث خفيف الوزن مزود بوقود من الهايدروجين مع مبرد مسبقاً[16]
محرك دورة الهواء السائل: محرك نفاث مزود بوقود من الهايدروجين يقوم بتسييل الهواء (يجعله سائلاً) قبل حرقه في محرك الصاروخ،
النفاثة الحفص-صدمية: محركات نفاثة تستعمل إحراق فوق الصوت.

مركبات الإطلاق الصاروخي العادية تحلق عموديا "تقريبا" قبل أن تعتدل أو تستوي أفقيا على ارتفاع يصل إلى بضع عشرات من الكيلوميترات قبل الإحراق الجوانب للدوران هذا الصعود العمودي الأولي يستهلك الوقود لكنه الأمثل حيث أنه يقلل مقاومة الهواء بشكل كبير.

تحرق المحركات الهوائية أو المحركات النفاثة الوقود بكفاءة عالية جداً وهذا قد يسمح بمسار انطلاق أكثر استواء بكثير المركبات تحلق عادة بشكل تماسي تقريبا مع سطح الأرض حتى تغادر الغلاف الجوي ثم تقوم بحرق صاروخ لتقريب فارق السرعة الأخير -دلتا في- من السرعة المدارية.

الوصول والإقلاع على سطح الكوكب

نسخة تجريبية لنظام أكياس الهواء لمركبة باثفايندر المتجهة للمريخ

حين توشك المركبة على الدخول إلى مدار الكوكب الذي ستنزل اليه أو إلى وجهتها المحددة عندما يحين وقت الإقلاع يجب تعديل مقدار سرعتها ويمكن فعل ذلك من خلال جميع الطرق المذكورة أعلاه (مما توفر قوة كافية من الدفع) لكن يوجد بعض الطرق التي تستفيد من الغلاف الجوي و/أو المسطحات.]]

كابح الدفع الهوائي يسمح للمركبة الفضائية الحدّ من نقطة ارتفاع المدار الأهليلجيي البيضاوي بواسطة فرش المتكررة مع الغلاف الجوي عند نقطة منخفضة للمدار ويمكن أن يتم تخزين كمية هائله من الوقود حيث أنها تأخذ نسبه قليله من الديلتا-في للدخول للمدار البيضاوي مقارنة بالمدار الدائري وبما أن الكبح يعمل به على عدة مدارات فإن التدفئة ثانويه نسبياً والدرع الواقي للحرارة غير مطلوب وقد تم العمل به في عدة بعثات إلى المريخ وتم إستخدامه في عدة مهمات إلى المريخ مثل مهمة مسح المريخ العالمية ومارس اوديسي ومسبار نارس ريكونيسيانس ومهمة فينيوس ماجلان.
اللاقط الهوائي يُعتبر أكثر من مناور هجومي، يقوم بالتحويل من المسار الإطنابي إلى مسار إهليجي في مدار واحد هذا يتطلب أوقية حرارية والمزيد من الملاحة الدقيقة في حال لابد أن تكون كاملة في عبور واحد خلال الجو والفرملة الطيرانية الغير متساوية لاتُوجد مشاهدة ممكنة للجو إذا كان الهدف للبقاء في مدار إذن على الأقل دفعة مناورة زائدة مطلوبة بعد اللاقط الهوائي في حالة آخرى النقطة الأقل للمدار الناتج ستبقى في الجو نتيجة إعادة الدخول النهائي.

اللاقط الهوائي لم يسبق له حتى الآن المحاولة لمهمة كوكبية لكن إعادة الإدخال تجاوز منطقة ستة ومنطقة سبعة في عودة القمر حيث مناورة اللاقط الهوائي منذ عودتهم حولوا المسار الإطنابي إلى مسار إهليجي في هذه المهمات منذ كان هناك لامحاولة لإحياء الحضيض القمري بعد الاقط الهوائي فالمدار الناتج متقاطع مع الجو وإعادة الإدخال ظهرت في الحضيض القمري المجاور.

الباليوت هو أداة كبح بسحب الهواء
المظلات حيث يمكن أن يهبط مسبار على كوكب أو قمر عبر الغلاف الجوي عادةً بعد تنقية الغلاف الجوي بإستخدام درع واقي من الحرارة
الوسائد الهوائية من الممكن أن تخفف الهبوط النهائة.
الكابح أو التوقف ببساطة من تحطيم الهدف، عادةً يتم عن طريق الصدفة ومع ذلك فإن من الممكن القيام بذلك عن قصد مع التحقيق المتوقع من البقاء على قيد الحياة (انظر، على سبيل المثال، الفضاء السحيق 2) في هذه الحالة الإستقصاء المتين والنهج منخفض السرعات هي المطلوبة.

الطرق الإفتراضي

هي مجموعة متنوعة من تقنيات الدفع الإفتراضية تم النظر إليها ودراستها والتي تتطلب مبادئ جديدة كليا ً في الفيزياء حتى تتحق وقد لا تكون موجودة حتى الآن مثل هذه الطرق تتسم بالمضاربة وتشمل [بحاجة لمصدر].

محرك قطري (diametric drive).
محرك النقز والتحيز (Pitch drive and bias drive).
محرك الانفصال (disjunction drive).
محرك ألكوبيير (Alcubierre drive، شكل من أشكال محرك الاعوجاج).
الشراع التفاضلي (Differential sail).
الثقوب الدودية (wormhole drive)، ممكن من الناحية النظرية لكن من ناحية الممارسة العملية غير قابل للتحقق مع التكنولوجيا الحالية
تأثير وودوارد (Woodward effect).
محرك بدون رد فعل (Reactionless drives)، يكسر قانون "حفظ الزخم" من المستحيل نظرياً.
محرك إم/ يحاول الإلتفاف على قانون الحفاظ على الزخم قد يكون من المستحيل نظرياً.
صاروخ فوتون (Photon rocket)
محرك الفضاء العالي (hyperspace drive)، محرك يستند على نظرية هايم.
مكرونيوتن دافع كهرومغناطيسي (Micronewton electromagnetic thruster)، يدعي إمكانية الحصول على الدافع بالطاقة الكهرومغناطيسية عن طريق فقدان الزخم الخطي.[1]

تم العثور على تقييم لوكالة ناسا في مارك ج ميليس في مقالة "تقييم التقدم العلمي للدفع المحتمل" (2005) وهو يقدم نظرة عامة على البحوث في وكالة ناسا في مشروع "فتوحات جديدة في فيزياء الدفع".

جدول الطرق

وهنا ملخص لبعض التكنولوجيات الأكثر رواجًا وتطورًا، ويتبعها أساليب فكرية متزايدة وهنالك أربعة أساليب

أولاً سرعة العادم الفعال وهو السرعة المعادلة التي يترك بها الإندفاع المركبة وهذه ليست بالضرورة أهم خاصية لأسلوب الدفع ولكن قد يكون الدفع واستهلاك الطاقة وعوامل أخرى أهم الخصائص ولكن،

إذا كانت الدلتا-v أكبر بكثير من عادم السرعة فمن الضروري جدًا وجود كميات كبيرة من الوقود (أنظر إلى جزء الحسابات في الأعلى)
إذا كان عادم السرعة أكبر بكثير من الدلتا-v فهي بحاجة لطاقة أكثر نسبيًا أما إذا كانت الطاقة محدودة كما هو الحال مع الطاقة الشمسية فهذا يعني أن الرحلة ستستغرق نسبيًا وقتا أطول.

الثانية والثالثة هي كميات نموذجيه من الدفع وحرق الوقت النموذجي للطريقة خارج الجاذبية كميات صغيرة محتملة لتطبيق الدفع على مدى فترة طويلة وسوف يعطي نفس تأثير الكميات الكبيرة اعتبارا من الدفع خلال فترة قصيرة (لا تنطبق هذه النتيجة عندما يتأثر كائن بشكل كبير من الجاذبية)

الرابع هو الحد الأقصى دلتا الخامس هذه التقنية يمكن أن تعطي (بدون التدريج) بالنسبة للصواريخ مثل أنظمة أجهزة االدفع هي وظيفة جزء من الشامل وسرعة العادم، الجزء الشامل للصواريخ مثل الأنظمة هي عادة محدودة بنظام الوزن والدفع ووزن الصهاريج ولنظام تحقيق هذا الحد ونموذجية الحمولة النافعة قد تحتاج إلى أن تكون نسبة مئوية ضئيلة من المركبة وبالتالي فإن الحد العملي على بعض الأنظمة يمكن أن يكون أقل من ذلك بكثير.

طرق الدفع
الطريقة	سرعة الفع الفعالة (كم/ث)	!الدفع (ن)	!فترة الأنطلاق	أقصى دلتا خمسة	مستوى الأستعداد التقني
صاروخ وقود صلب	<~ 2.5	<~ 10⁷	دقائق	7000700000000000000♠~ 7	9:برهنة طيرانية
صاروخ متلين			دقائق	7000300000000000000♠> 3	9:برهنة طيرانية
صاروخ دفع أحادي	7000200000000000000♠1 – 3^{[بحاجة لمصدر]}	7000316227766016840♠0.1 – 100^{[بحاجة لمصدر]}	ميليثانية - دقائق	7000300000000000000♠~ 3	9:برهنة طيرانية
صاروخ وقود سائل	<~ 4.4	<~ 10⁷	دقائق	7000900000000000000♠~ 9	9:برهنة طيرانية
دافع أيوني الكسترستاتيكي	7002112500000000000♠15 – 210[17]^{[استشهاد منقوص البيانات]}		أشهر/سنوات	7002100000000000000♠> 100	9:برهنة طيرانية
دافع هيت	7001290000000000000♠8–50^{[بحاجة لمصدر]}		أشهر/سنوات	7002100000000000000♠> 100	9:برهنة طيرانية
صاروخ دفع مقاوم	7000400000000000000♠2–6	6999316227766016840♠10⁻²–10	دقائق	?	8:مؤهلة للطيران[18]
صاروخ أركدجت	7001100000000000000♠4–16	6999316227766016840♠10⁻²–10	دقائق	?	8:مؤهلة للطيران
دفع مجال ابعاث كهربائي (FEEP)	7002115000000000000♠100[19]–130	6995316227766016840♠10⁻⁶[20]–10⁻³[20]	أشهر/سنوات	?	8:مؤهلة للطيران[20]
دافع بلازمة نابضة (PPT)	7001200000000000000♠~ 20	6999100000000000000♠~ 0.1	من 2000 وحتى 10000 ساعة	?	7:عرض نموذج في الفضاء
صاروخ دفع ثنائي التشغيل	7000285000000000000♠1 – 4.7	7003100000000000000♠0.1 – 10⁷	ميليثانية - دقائق	7000600000000000000♠~ 3 – 9	7:عرض نموذج في الفضاء
أشرعة شمسية	299792:Light ريح شمسية	9/km² at 1 وحدة فلكية 230/km² at 0.2AU 10⁻¹⁰/km² at 4 سنة ضوئية	غير محدد	7001400000000000000♠> 40	7000666700000000000♠9:برهنة تجربة طيران في ضغط جو خفيف 6:تطبيق فضائي 5:برهنة في تشريع خفيف
صاروخ ثلاثي الدفع	7000390000000000000♠2.5–5.3^{[بحاجة لمصدر]}	7003100000000000000♠0.1–10⁷^{[بحاجة لمصدر]}	دقائق	7000900000000000000♠~ 9	6:Prototype برهنة نموذج على الأرض[21]
دفع بلازمي مغناطيسي ديناميكي(MPD)	7001600000000000000♠20–100	100	أسابيع	?	6:تجربة نموذج 1 في الفضاء[22]
صاروخ حرارة نووية	9[23]	7007100000000000000♠10⁷[24]	7001600000000000000♠دقائق [24]	7001200000000000000♠> ~ 20	6:برهنة نموذج على الأرض
دوافع كتلة	7001150000000000000♠0–~30	7006100000000000000♠10⁴–10⁸	أشهر	?	6:تجربة نموذج 32أم جاي على الأرض
دافع ثيلر	N/A	7006100000000000000♠1–10¹²	دقائق	7000700000000000000♠~ 7	6:نموذج 31.7 في الفضاء in space[25]
صاروخ مدمج هوائي	7000550000000000000♠5–6	7003100000000000000♠0.1–10⁷	ثواني - دقائق	7000700000000000000♠> 7?	6:تجربة نموذج على الأرض[26][27]
محرك دوران هواء سائل	4٫5	7005100000000000000♠10³–10⁷	ثواني - دقائق	?	6:تجربة نموذج على الأرض
دافع استقراضي نابض (PIT)	7001450000000000000♠10[28]–80[28]	20	أشهر	?	5:برهنة عنصر في الفضاء[28]
صاروخ نبض محدد متغير بالبلازمة الممغنطة (VASIMR)	7002155000000000000♠10–300^{[بحاجة لمصدر]}	7002620000000000000♠40–1,200^{[بحاجة لمصدر]}	أيام - أشهر	7002100000000000000♠> 100	5:برهنة عنصر 200 كو في الفضاء
دفع مكبر لمجال مغناطيسي نابض	7001700000000000000♠10–130	6999316227766016840♠0.1–1	أيام - أشهر	7002100000000000000♠> 100	5:برهنة عنصر في الفضاء
صاروخ حرارة شمسية	7000950000000000000♠7–12	7001100000000000000♠1–100	أسابيع	7001200000000000000♠> ~ 20	4:برهنة عنصر في المختبر[29]
صاروخ راديو أيزوتوبي	7000750000000000000♠7–8^{[بحاجة لمصدر]}	7000140000000099999♠1.3–1.5	أشهر	?	4:برهنة عنصر في المختبر
صاروخ كهراء نووية	Variable	Variable	متغير	?	4:برهنة عنصر400 كو في المختبر
مشروع أوريون	7001600000000000000♠20–100	7010316227766016840♠10⁹–10¹²	عدة أيام	7001450000000000000♠~30–60	3:مبرهنة - أثبات فكرة 900كغ [30][31]
مصعد الفضاء	N/A	N/A	غير محدد	7001120000000000000♠> 12	3:مبرهنة - أثبات فكرة
محرك انفعاليSABRE[1]	7001172500000000000♠30/4.5	7003100000000000000♠0.1–10⁷	دقائق	9٫4	3:مبرهنة - أثبات فكرة
أشرعة مغناطيسية	7002447500000000000♠ريح شمسية	70/40طن[32]	غير محدد	?	3:مبرهنة - أثبات فكرة
دافع مغنطيس داؤري مصغر	200	7002400000000000000♠~1 N/kW	أشهر	?	3:مبرهنة - أثبات فكرة[33]
لايزر/أشعة طاقة	Variable	Variable	متغير	?	3:مبرهنة - أثبات فكرة 71 م
حلقة انطلاق/حلقة مدارية	N/A	7004100000000000000♠~10⁴	دقائق	7001205000000000000♠>>11–30	2:تطبيق معادلة الفكرة التقنية
محرك نبض نووي (مشروع دايدالوس	7002510000000000000♠20–1,000	7010316227766016840♠10⁹–10¹²	سنوات	7004150000000000000♠~15,000	2:تطبيق معادلة الفكرة التقنية
صاروخ ذو قلب غازي	7001150000000000000♠10–20	7004316227766016840♠10³–10⁶	?	?	2:تطبيق معادلة الفكرة التقنية
صاروخ ماء مالح نووي	100	7005100000000000000♠10³–10⁷	نصف ساعة	?	2:تطبيق معادلة الفكرة التقنية
شراع انشطاري	?	?	?	?	2:تطبيق معادلة الفكرة التقنية
صاروغ مشرذمات انشطارية	15٬000	?	?	?	2:تطبيق معادلة الفكرة التقنية
صاروخ فوتوني نووي	299٬792	6997316227766016840♠10⁻⁵–1	سنوات - عقود	?	2:تطبيق معادلة الفكرة التقنية
صاروخ اندماجي	7002550000000000000♠100–1,000^{[بحاجة لمصدر]}	?	?	?	2:تطبيق معادلة الفكرة التقنية
دفع نووي بنبض حافز	7003210000000000000♠200–4,000	?	أيام - أسابع	?	2:تطبيق معادلة الفكرة التقنية
صاروخ مضاد للمادة	7004550000000000000♠10,000–100,000^{[بحاجة لمصدر]}	?	?	?	2:تطبيق معادلة الفكرة التقنية
رامجيت بوسارد	7004100011000000000♠2.2–20,000	?	غير محدد	7004300000000000000♠~30,000	2:تطبيق معادلة الفكرة التقنية
الطريقة	سرعة الدفع الفعالة (كم/ث)	!الدفع (ن)	!فترة الأنطلاق	أقصى دلتا خمسة	مستوى الأستعداد التقني

الاختبار

تختبر أنظمة دفع المركبة الفضائية أولاً بشكل ثابت على سطح الأرض داخل نطاق الغلاف الجوي، ولكن العديد من الأنظمة تتطلب فجوة فارغة للاختبار بشكل تام، وتختبر الصواريخ عادةً على مرفق اختبار محرك الصواريخ بشكل جيد وبعيداً عن الإسكان والمباني الأخرى لأسباب أمنية، وتعتبر محركات أيون أقل خطراً وتتطلب القليل من السلامة وعادةً الفجوة الفارغة الكبيرة هي المتطلبة فقط.

ويمكن إيجاد أشهر موقع اختبار ثابت في مرافق اختبار الصواريخ الأرضية، وبعض الأنظمة لا يمكن اختبارها على الأرض بشكل كاف ويمكن استخدام اختبار إطلاق الصواريخ في موقع الإطلاق.

للإستزادة

المراجع

Dimitri S.H. Charrier (2012). "Micronewton electromagnetic thruster". Applied Physics Letters. 101. صفحة 034104. مؤرشف من الأصل في 6 مايو 2020. الوسيط |CitationClass= تم تجاهله (مساعدة)
Phillips, Tony (May 30, 2000). "Solar S'Mores". NASA. مؤرشف من الأصل في 13 يناير 2010. اطلع عليه بتاريخ 30 يوليو 2007. الوسيط |CitationClass= تم تجاهله (مساعدة)
Olsen, Carrie (September 21, 1995). "Hohmann Transfer & Plane Changes". NASA. مؤرشف من الأصل في 15 يوليو 2007. اطلع عليه بتاريخ 30 يوليو 2007. الوسيط |CitationClass= تم تجاهله (مساعدة)
Staff (April 24, 2007). "Interplanetary Cruise". 2001 Mars Odyssey. NASA. مؤرشف من الأصل في 25 أغسطس 2009. اطلع عليه بتاريخ 30 يوليو 2007. الوسيط |CitationClass= تم تجاهله (مساعدة) ^{[وصلة مكسورة]}
Doody, Dave (February 7, 2002). "Chapter 4. Interplanetary Trajectories". Basics of Space Flight. NASA JPL. مؤرشف من الأصل في 16 أغسطس 2015. اطلع عليه بتاريخ 30 يوليو 2007. الوسيط |CitationClass= تم تجاهله (مساعدة)
Hoffman, S. (August 20–22, 1984). "A comparison of aerobraking and aerocapture vehicles for interplanetary missions". AIAA and AAS, Astrodynamics Conference. Seattle, Washington: American Institute of Aeronautics and Astronautics. صفحات 25 p. مؤرشف من الأصل في 24 نوفمبر 2011. اطلع عليه بتاريخ 31 يوليو 2007. الوسيط |CitationClass= تم تجاهله (مساعدة)
Anonymous (2007). "Basic Facts on Cosmos 1 and Solar Sailing". The Planetary Society. مؤرشف من الأصل في 29 فبراير 2012. اطلع عليه بتاريخ 26 يوليو 2007. الوسيط |CitationClass= تم تجاهله (مساعدة)
Rahls, Chuck (December 7, 2005). "Interstellar Spaceflight: Is It Possible?". Physorg.com. مؤرشف من الأصل في 1 مارس 2012. اطلع عليه بتاريخ 31 يوليو 2007. الوسيط |CitationClass= تم تجاهله (مساعدة)
Zobel, Edward A. (2006). "Summary of Introductory Momentum Equations". Zona Land. مؤرشف من الأصل في 21 فبراير 2010. اطلع عليه بتاريخ 02 أغسطس 2007. الوسيط |CitationClass= تم تجاهله (مساعدة)
Benson, Tom. "Guided Tours: Beginner's Guide to Rockets". NASA. مؤرشف من الأصل في 14 أغسطس 2013. اطلع عليه بتاريخ 02 أغسطس 2007. الوسيط |CitationClass= تم تجاهله (مساعدة)
equation 19-1 Rocket propulsion elements 7th edition- Sutton
King-Hele, Desmond (1987). Satellite orbits in an atmosphere: Theory and application. Springer. ISBN 978-0-216-92252-5. مؤرشف من الأصل في 24 ديسمبر 2016. اطلع عليه بتاريخ 10 يناير 2015. الوسيط |CitationClass= تم تجاهله (مساعدة)
Tsiotras, P. (2001). "Satellite attitude control and power tracking with energy/momentum wheels". Journal of Guidance, Control, and Dynamics. 43 (1): 23–34. Bibcode:2001JGCD...24...23T. doi:10.2514/2.4705. ISSN 0731-5090. الوسيط |CitationClass= تم تجاهله (مساعدة)
Dykla, J. J.; Cacioppo, R.; Gangopadhyaya, A. (2004). "Gravitational slingshot". American Journal of Physics. 72 (5): 619–000. Bibcode:2004AmJPh..72..619D. doi:10.1119/1.1621032. الوسيط |CitationClass= تم تجاهله (مساعدة)
Anonymous (2006). "The Sabre Engine". Reaction Engines Ltd. مؤرشف من الأصل في 17 أكتوبر 2016. اطلع عليه بتاريخ 26 يوليو 2007. الوسيط |CitationClass= تم تجاهله (مساعدة)
Harada, K.; Tanatsugu, N.; Sato, T. (1997). "Development Study on ATREX Engine". Acta Astronautica. 41 (12): 851–862. doi:10.1016/S0094-5765(97)00176-8. الوسيط |CitationClass= تم تجاهله (مساعدة)صيانة CS1: أسماء متعددة: قائمة المؤلفون (link)
ESA Portal – ESA and ANU make space propulsion breakthrough نسخة محفوظة 03 ديسمبر 2012 على موقع واي باك مشين.
A Xenon Resistojet Propulsion System for Microsatellites (Surrey Space Centre, University of Surrey, Guildford, Surrey)
Alta - Space Propulsion, Systems and Services - Field Emission Electric Propulsion نسخة محفوظة 16 أكتوبر 2015 على موقع واي باك مشين.
(بالإنجليزية)Alta - Space Propulsion, Systems and Services - Field Emission Electric Propulsion نسخة محفوظة 16 أكتوبر 2015 على موقع واي باك مشين.
RD-701 نسخة محفوظة 09 يوليو 2006 على موقع واي باك مشين.
Google Translate نسخة محفوظة 28 أبريل 2019 على موقع واي باك مشين.
RD-0410 نسخة محفوظة 12 فبراير 2017 على موقع واي باك مشين.
(بالإنجليزية)RD-0410 نسخة محفوظة 12 فبراير 2017 على موقع واي باك مشين.
Young Engineers' Satellite 2 نسخة محفوظة 23 سبتمبر 2017 على موقع واي باك مشين.
Gnom نسخة محفوظة 13 يونيو 2006 على موقع واي باك مشين.
NASA GTX نسخة محفوظة 22 نوفمبر 2008 على موقع واي باك مشين. ^{[وصلة مكسورة]}
The PIT MkV pulsed inductive thruster نسخة محفوظة 11 فبراير 2014 على موقع واي باك مشين.
Pratt & Whitney Rocketdyne Wins $2.2 Million Contract Option for Solar Thermal Propulsion Rocket Engine (Press release, June 25, 2008, Pratt & Whitney Rocketdyne) نسخة محفوظة 28 أبريل 2019 على موقع واي باك مشين. ^{[وصلة مكسورة]}
"Operation Plumbbob". يوليو 2003. مؤرشف من الأصل في 31 ديسمبر 2018. اطلع عليه بتاريخ 31 يوليو 2006. الوسيط |CitationClass= تم تجاهله (مساعدة)
Brownlee, Robert R. (يونيو 2002). "Learning to Contain Underground Nuclear Explosions". مؤرشف من الأصل في 6 يونيو 2019. اطلع عليه بتاريخ 31 يوليو 2006. الوسيط |CitationClass= تم تجاهله (مساعدة)
PSFC/JA-05-26:Physics and Technology of the Feasibility of Plasma Sails, Journal of Geophysical Research, September 2005 نسخة محفوظة 24 سبتمبر 2015 على موقع واي باك مشين.
MagBeam نسخة محفوظة 03 يناير 2013 على موقع واي باك مشين.

بوابة الفضاء
بوابة رحلات فضائية

في كومنز صور وملفات عن: قوة دفع المركبة الفضائية

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.

[Applied_Physics_Letters-1] Dimitri S.H. Charrier (2012). "Micronewton electromagnetic thruster". Applied Physics Letters. 101. صفحة 034104. مؤرشف من الأصل في 6 مايو 2020. الوسيط |CitationClass= تم تجاهله (مساعدة)

[2] Phillips, Tony (May 30, 2000). "Solar S'Mores". NASA. مؤرشف من الأصل في 13 يناير 2010. اطلع عليه بتاريخ 30 يوليو 2007. الوسيط |CitationClass= تم تجاهله (مساعدة)

[3] Olsen, Carrie (September 21, 1995). "Hohmann Transfer & Plane Changes". NASA. مؤرشف من الأصل في 15 يوليو 2007. اطلع عليه بتاريخ 30 يوليو 2007. الوسيط |CitationClass= تم تجاهله (مساعدة)

[4] Staff (April 24, 2007). "Interplanetary Cruise". 2001 Mars Odyssey. NASA. مؤرشف من الأصل في 25 أغسطس 2009. اطلع عليه بتاريخ 30 يوليو 2007. الوسيط |CitationClass= تم تجاهله (مساعدة) ^{[وصلة مكسورة]}

[5] Doody, Dave (February 7, 2002). "Chapter 4. Interplanetary Trajectories". Basics of Space Flight. NASA JPL. مؤرشف من الأصل في 16 أغسطس 2015. اطلع عليه بتاريخ 30 يوليو 2007. الوسيط |CitationClass= تم تجاهله (مساعدة)

[6] Hoffman, S. (August 20–22, 1984). "A comparison of aerobraking and aerocapture vehicles for interplanetary missions". AIAA and AAS, Astrodynamics Conference. Seattle, Washington: American Institute of Aeronautics and Astronautics. صفحات 25 p. مؤرشف من الأصل في 24 نوفمبر 2011. اطلع عليه بتاريخ 31 يوليو 2007. الوسيط |CitationClass= تم تجاهله (مساعدة)

[7] Anonymous (2007). "Basic Facts on Cosmos 1 and Solar Sailing". The Planetary Society. مؤرشف من الأصل في 29 فبراير 2012. اطلع عليه بتاريخ 26 يوليو 2007. الوسيط |CitationClass= تم تجاهله (مساعدة)

[8] Rahls, Chuck (December 7, 2005). "Interstellar Spaceflight: Is It Possible?". Physorg.com. مؤرشف من الأصل في 1 مارس 2012. اطلع عليه بتاريخ 31 يوليو 2007. الوسيط |CitationClass= تم تجاهله (مساعدة)

[9] Zobel, Edward A. (2006). "Summary of Introductory Momentum Equations". Zona Land. مؤرشف من الأصل في 21 فبراير 2010. اطلع عليه بتاريخ 02 أغسطس 2007. الوسيط |CitationClass= تم تجاهله (مساعدة)

[beginners_guide-10] Benson, Tom. "Guided Tours: Beginner's Guide to Rockets". NASA. مؤرشف من الأصل في 14 أغسطس 2013. اطلع عليه بتاريخ 02 أغسطس 2007. الوسيط |CitationClass= تم تجاهله (مساعدة)

[sutton13-11] quation 19-1 Rocket propulsion elements 7th edition- Sutton

[12] King-Hele, Desmond (1987). Satellite orbits in an atmosphere: Theory and application. Springer. ISBN 978-0-216-92252-5. مؤرشف من الأصل في 24 ديسمبر 2016. اطلع عليه بتاريخ 10 يناير 2015. الوسيط |CitationClass= تم تجاهله (مساعدة)

[13] Tsiotras, P. (2001). "Satellite attitude control and power tracking with energy/momentum wheels". Journal of Guidance, Control, and Dynamics. 43 (1): 23–34. Bibcode:2001JGCD...24...23T. doi:10.2514/2.4705. ISSN 0731-5090. الوسيط |CitationClass= تم تجاهله (مساعدة)

[14] Dykla, J. J.; Cacioppo, R.; Gangopadhyaya, A. (2004). "Gravitational slingshot". American Journal of Physics. 72 (5): 619–000. Bibcode:2004AmJPh..72..619D. doi:10.1119/1.1621032. الوسيط |CitationClass= تم تجاهله (مساعدة)

[SABRE2-15] Anonymous (2006). "The Sabre Engine". Reaction Engines Ltd. مؤرشف من الأصل في 17 أكتوبر 2016. اطلع عليه بتاريخ 26 يوليو 2007. الوسيط |CitationClass= تم تجاهله (مساعدة)

[16] Harada, K.; Tanatsugu, N.; Sato, T. (1997). "Development Study on ATREX Engine". Acta Astronautica. 41 (12): 851–862. doi:10.1016/S0094-5765(97)00176-8. الوسيط |CitationClass= تم تجاهله (مساعدة)صيانة CS1: أسماء متعددة: قائمة المؤلفون (link)

[17] ESA Portal – ESA and ANU make space propulsion breakthrough نسخة محفوظة 03 ديسمبر 2012 على موقع واي باك مشين.

[18] A Xenon Resistojet Propulsion System for Microsatellites (Surrey Space Centre, University of Surrey, Guildford, Surrey)

[feep-19] Alta - Space Propulsion, Systems and Services - Field Emission Electric Propulsion نسخة محفوظة 16 أكتوبر 2015 على موقع واي باك مشين.

[مولد_تلقائيا1-20] (بالإنجليزية)Alta - Space Propulsion, Systems and Services - Field Emission Electric Propulsion نسخة محفوظة 16 أكتوبر 2015 على موقع واي باك مشين.

[21] RD-701 نسخة محفوظة 09 يوليو 2006 على موقع واي باك مشين.

[22] Google Translate نسخة محفوظة 28 أبريل 2019 على موقع واي باك مشين.

[rd0410-23] RD-0410 نسخة محفوظة 12 فبراير 2017 على موقع واي باك مشين.

[مولد_تلقائيا2-24] (بالإنجليزية)RD-0410 نسخة محفوظة 12 فبراير 2017 على موقع واي باك مشين.

[Tether-25] Young Engineers' Satellite 2 نسخة محفوظة 23 سبتمبر 2017 على موقع واي باك مشين.

[26] Gnom نسخة محفوظة 13 يونيو 2006 على موقع واي باك مشين.

[27] NASA GTX نسخة محفوظة 22 نوفمبر 2008 على موقع واي باك مشين. ^{[وصلة مكسورة]}

[PIT-28] The PIT MkV pulsed inductive thruster نسخة محفوظة 11 فبراير 2014 على موقع واي باك مشين.

[29] Pratt & Whitney Rocketdyne Wins $2.2 Million Contract Option for Solar Thermal Propulsion Rocket Engine (Press release, June 25, 2008, Pratt & Whitney Rocketdyne) نسخة محفوظة 28 أبريل 2019 على موقع واي باك مشين. ^{[وصلة مكسورة]}

[30] "Operation Plumbbob". يوليو 2003. مؤرشف من الأصل في 31 ديسمبر 2018. اطلع عليه بتاريخ 31 يوليو 2006. الوسيط |CitationClass= تم تجاهله (مساعدة)

[31] Brownlee, Robert R. (يونيو 2002). "Learning to Contain Underground Nuclear Explosions". مؤرشف من الأصل في 6 يونيو 2019. اطلع عليه بتاريخ 31 يوليو 2006. الوسيط |CitationClass= تم تجاهله (مساعدة)

[32] PSFC/JA-05-26:Physics and Technology of the Feasibility of Plasma Sails, Journal of Geophysical Research, September 2005 نسخة محفوظة 24 سبتمبر 2015 على موقع واي باك مشين.

[33] MagBeam نسخة محفوظة 03 يناير 2013 على موقع واي باك مشين.