عمر النصف
عمر النصف رمزه (t1⁄2) لمادة نشيطة إشعاعيا هو مقدار الوقت اللازم للكمية، لتنخفض إلى نصف قيمتها كما تم قياسها في بداية الفترة الزمنية لتحلل إشعاعي .[1][2][3] يتسم كل نظير مشع بنصف عمر مميز له، ونجد أنواعا من النظائر المشعة لها عمر النصف يبلغ إلى ثوان أو ميلي ثانية أو أقل، وأخرى لها عمر النصف يبلغ ألاف السنين، وأخرى لها عمر النصف يبلغ حتى ملايين أو مليارات السنين.
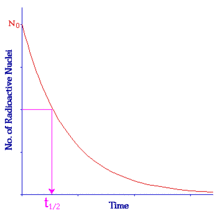
تتبع معادلة التحلل الإشعاعي التحلل الأسي. وتكون فترة عمر النصف هو الزمن اللازم لتحلل نصف كمية المادة، وذلك بصرف النظر عن كون العينة 1 جرام أو 1000 جرام، فهو زمن ثابت يميز النظير المشع مهما كانت كميته.
في الشكل يتبين أنه بعد انقضاء عمر النصف، أي عند الزمن t1⁄2 نجد أن الجزء الباقي من المادة ولم يتحلل قد بلغ النصف. وإذا انتظرنا مدة تالية قدرها t1⁄2 نجد أن كمية المادة التي لم تتحلل بعد مقدارها نصف عمر النصف، أي ربع الكمية الأصلية . وإذا انتظرنا مدة ثالثة قدرها t1⁄2 نجد أن الكمية التي لم تتحلل أصبحت 1/8 الكمية الأصلية وهكذا.
الجدول الموجود في الأسفل يعطي نسبة الباقى من المادة على أساس فترات متتالية من عمر النصف لتحلل المادة.
| عدد الأعمار النصفية المنقضية | الجزء المتبقي | النسبة المئوية المتبقية |
|---|---|---|
| 0 | 1⁄1 | 100 |
| 1 | 1⁄2 | 50 |
| 2 | 1⁄4 | 25 |
| 3 | 1⁄8 | 12,5 |
| 4 | 1⁄16 | 6,25 |
| 5 | 1⁄32 | 3,125 |
| 6 | 1⁄64 | 1,563 |
| 7 | 1⁄128 | 0,781 |
| ... | ... | ... |
| n | 1/2n | 100⁄(2n) |
تحلل نظير مشع
نفترض أن كمية نظير مشع عند الزمن t=0 ، فيمكننا حساب الكمية التي بقت دون تحلل خلال الزمن t من المعادلة:
حيث
- هي القيمة الأصلية ل N (عند t=0)
- λ ثابت موجب(ثابت التحلل).
عندما تكون t=0, تكون الدالة الأسية 1، وتكون مساوية لـ. عندما t تقترب من اللانهاية، تقترب الدالة الأسية من الصفر. عند تحلل نصف الكمية فإنه يوجد وقت تصبح:
وبالتعويض في المعادلة السابقة نحصل على :
وعلى هذا فإن فترة عمر النصف تكون 69.3% من متوسط عمر النصف.
التحلل بطريقتين أو أكثر
العنصر النشيط إشعاعيا يمكن أن يتحلل بطريقتين أو أكثر . وهذه الطرق لها إمكانيات مختلفة لحدوثها، ولذا فإن لكل منها فترة عمر نصف خاصة بها .
فمثلا لنظامين من أنظمة التحلل، فإن كمية المادة المتبقية بعد زمن قدره t يتم حسابها من المعادلة :
وبنفس النظام المتبع في القسم السابق، يمكن حساب عمر النصف النهائي الجديد كالتالى :
أو بالتعبير عنه بواسطة فترتي عمر النصف :
حيث فترة عمر النصف بالطريقة الأولى فترة عمر النصف بالطريقة الثانية .
موضوعات متعلقة
مراجع
- Lin VW; Cardenas DD (2003). Spinal cord medicine. Demos Medical Publishing, LLC. صفحة 251. ISBN 1-888799-61-7. مؤرشف من الأصل في 26 يناير 2020. الوسيط
|CitationClass=تم تجاهله (مساعدة) - Wallin, John (September 1996). "Assignment #2: Data, Simulations, and Analytic Science in Decay". Astro.GLU.edu. مؤرشف من الأصل في 29 سبتمبر 2011. الوسيط
|CitationClass=تم تجاهله (مساعدة) - "Radioactive-Decay Model". Exploratorium.edu. مؤرشف من الأصل في 16 أكتوبر 2015. اطلع عليه بتاريخ 25 أبريل 2012. الوسيط
|CitationClass=تم تجاهله (مساعدة)
- بوابة الكيمياء
- بوابة الفيزياء
- بوابة كيمياء فيزيائية
